Matlab LS-SVM工具箱实战应用指南

本文还有配套的精品资源，点击获取

简介：LS-SVM是一种用于非线性分类和回归问题的机器学习模型，Matlab的LS-SVM1.5工具箱让研究人员和工程师能方便地在Matlab环境中实现该算法。工具箱通过最小化平方误差构建决策边界，可能在处理过拟合时表现更佳。其主要功能包括模型训练、参数优化、预测与评估、数据可视化、应用示例以及文档支持。对于初学者而言，附带的示例脚本和详尽文档是非常有帮助的资源。掌握LS-SVM工具箱，用户可以解决多种实际工程问题。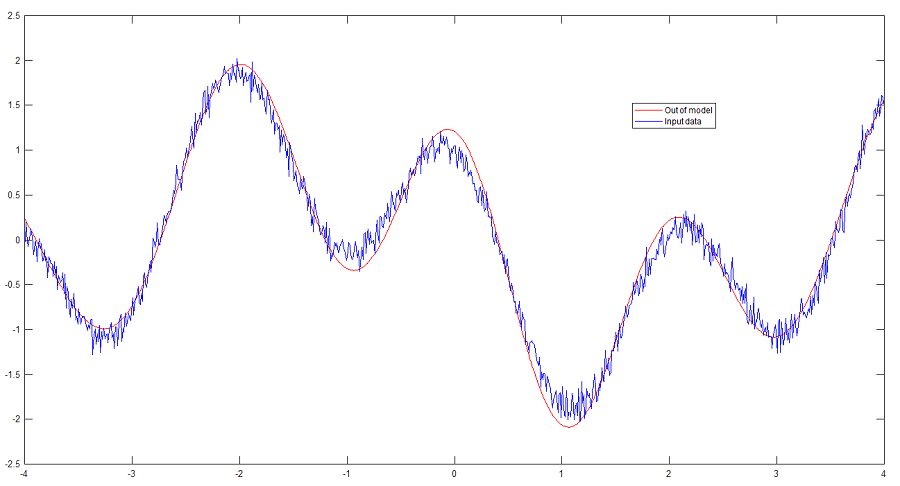

1. LS-SVM模型概述

支持向量机（SVM）是机器学习领域中一种强大的分类和回归算法，其在小样本学习情境下表现尤为突出。最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM）作为SVM的一种变体，通过优化问题的二次规划转化为线性方程求解，从而减少了计算复杂度和提高了求解速度。

1.1 LS-SVM的发展背景

LS-SVM在传统SVM的基础上进行了改进，其核心在于将SVM的不等式约束转换为等式约束，并通过引入最小二乘法原理来简化优化问题。这种方法不仅加快了求解过程，还保持了SVM在分类准确性上的优势。

1.2 LS-SVM的基本原理

LS-SVM在处理回归问题时，通过最小化残差平方和的方式来逼近理想决策函数。其模型参数通过求解一个线性方程组得到，从而避免了传统SVM中复杂的二次规划问题求解过程。

1.3 LS-SVM的应用范围

LS-SVM在众多领域中都有广泛的应用，如生物信息学、金融、通信等。它特别适合于解决具有非线性边界和高维数据的问题，因此在工程应用中有着不可替代的地位。

在本章中，我们对LS-SVM的发展背景、基本原理和应用范围进行了概览，为理解后续章节中如何使用Matlab LS-SVM工具箱进行具体操作打下了基础。接下来，我们将详细探究如何安装和配置Matlab LS-SVM工具箱，以便在实际工作中应用这一强大的模型。

2. Matlab LS-SVM1.5工具箱介绍

2.1 工具箱的安装与配置

2.1.1 安装过程详解

安装Matlab LS-SVM1.5工具箱是一个相对简单的过程，但需确保安装环境满足特定的系统要求。工具箱支持在多种Matlab版本上运行，例如Matlab R2015a或更高版本。下面是安装步骤：

1. 下载最新版本的LS-SVM1.5工具箱，通常可以访问工具箱的官方网站或者在Matlab的File Exchange中找到。
2. 解压下载的文件到一个文件夹中。注意：解压路径最好不要包含中文字符或者空格，以避免兼容性问题。
3. 打开Matlab，使用 addpath 函数添加包含工具箱的文件夹路径到Matlab的路径列表中。例如：

addpath('C:\Path\To\LS-SVM1.5');

1. 在Matlab命令窗口中输入 ls 并回车，检查工具箱的函数和脚本是否能够被正确识别。

此步骤确保了在后续使用中，Matlab能调用工具箱中的所有函数，从而避免 Undefined function or variable 的错误。

2.1.2 配置环境及依赖

工具箱的配置不仅仅局限于路径的添加。还需要确保Matlab环境变量正确配置，如：

• 确保Matlab安装了必要的编译器，因为LS-SVM1.5工具箱某些功能可能需要进行本地代码的编译。
• 如果是并行计算的场景，需要配置好Matlab的并行计算工具箱。
• 对于一些依赖于特定Matlab工具箱的功能，如信号处理工具箱，需要提前安装。

一个典型的配置过程可能如下所示：

% 检查并安装必要的工具箱依赖，例如Parallel Computing Toolbox
if ~exist('parfor', 'file')
    disp('安装并行计算工具箱...');
    toolbox = 'Parallel Computing Toolbox';
    disp(['正在安装工具箱: ' toolbox]);
    toolboxinstaller.addToolbox(toolbox);
    disp('安装完成');
else
    disp('工具箱已经安装');
end

2.2 工具箱的结构与功能概览

2.2.1 核心文件与模块划分

LS-SVM1.5工具箱的核心文件包括核心函数、数据结构、以及执行各种算法的脚本。模块的划分如下：

• 初始化模块 ：包括创建LS-SVM模型、初始化参数等。
• 优化模块 ：包含训练算法，如序列最小优化（SMO）算法。
• 评估模块 ：评估训练好的模型性能，如交叉验证。
• 数据预处理模块 ：包括数据标准化、归一化等功能。
• 可视化模块 ：提供决策边界和模型性能的可视化展示。

2.2.2 工具箱支持的算法类型

LS-SVM1.5工具箱支持多种算法，主要以最小二乘支持向量机（LS-SVM）为基础，同时支持一些改进的变体，例如：

• 基本LS-SVM用于回归问题。
• 对于分类问题，可以使用归一化的LS-SVM（NLS-SVM）。
• 结合核函数的方法，以处理非线性问题，如径向基函数（RBF）核、多项式核等。

每种算法都有相应的参数设置，以适应不同的问题和优化目标。下面的代码块展示了如何列出工具箱中所有可用的算法：

% 列出工具箱中所有可用的算法
algorithms = dir('*.m'); % 假定每个算法对应一个.m文件
algorithm_list = {algorithms.name}';
disp('支持的算法列表：');
disp(algorithm_list);

工具箱的核心功能为LS-SVM的训练和预测提供了一个灵活的接口，能够适应各种机器学习和数据挖掘任务的需求。

3. 最小化平方误差决策边界构建

3.1 LS-SVM的数学基础

3.1.1 核技巧与非线性映射

最小二乘支持向量机（LS-SVM）利用核技巧处理非线性问题，它将输入数据映射到高维空间，使原本在低维空间中线性不可分的数据变得线性可分。核技巧的关键在于核函数的选取，它能够有效地计算出输入空间中任意两个数据点在高维空间的内积。

核函数通常包括线性核、多项式核、径向基函数（RBF）核和Sigmoid核等。例如，RBF核，也称为高斯核，其数学表达式如下：

K(x_i, x_j) = exp(-γ \| x_i - x_j \|^2)

这里，( \gamma ) 是一个可调节的参数，控制着映射后空间的复杂度。高维空间中的内积运算可以通过RBF核在原始空间中直接计算完成，这避免了高维空间中复杂的直接计算。

3.1.2 约束优化问题的平方损失函数

在LS-SVM中，通常采用二次规划方法来求解支持向量机的优化问题。损失函数由传统的Hinge损失转变为平方损失，其优化问题表述如下：

最小化：

J(w, \xi) = \frac{1}{2} \| w \|^2 + \frac{1}{2} C \sum_{i=1}^{N} \xi_i^2

受约束于：

y_i(w \cdot x_i + b) = 1 - \xi_i, \quad \xi_i \geq 0, \quad i=1, \ldots, N

这里，( w ) 是权值向量，( b ) 是偏置项，( \xi_i ) 是松弛变量，( C ) 是正则化参数，控制着对错分样本的惩罚程度。通过求解这个优化问题，可以得到决策函数：

f(x) = w \cdot \phi(x) + b

其中，( \phi(x) ) 是非线性映射函数。

3.2 构建最小化平方误差的算法流程

3.2.1 优化问题的求解方法

LS-SVM的优化问题可以通过引入拉格朗日乘数法转换成对偶问题求解。在对偶问题中，我们不再直接求解( w )和( b )，而是通过求解拉格朗日乘数( \alpha )来得到它们。对偶问题的目标函数变为：

最小化：

L(\alpha) = \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{N} \alpha_i \alpha_j y_i y_j K(x_i, x_j)

受约束于：

\sum_{i=1}^{N} \alpha_i y_i = 0, \quad 0 \leq \alpha_i \leq C, \quad i=1, \ldots, N

这个问题可以通过解析方法或者数值优化方法求解。

3.2.2 约束条件的处理技巧

在优化问题中，约束条件起着重要的作用。特别是在支持向量机中，约束条件帮助确定支持向量，并且影响模型的复杂度和泛化能力。处理约束条件的一个常见方法是使用二次规划（QP）算法，例如序列最小优化（SMO）算法。SMO算法将大规模的QP问题分解为一系列最小的问题，每次只考虑两个拉格朗日乘数，从而简化了计算复杂度。

在实际操作中，通常使用现成的数值优化库来处理这些约束条件。例如，在Matlab环境中，可以使用 quadprog 函数来求解上述对偶问题。此外，还可以根据具体问题选择适合的数值优化算法，如梯度下降法、牛顿法等。

通过上述内容，我们可以看到，最小化平方误差决策边界的构建是通过将优化问题转化为对偶问题，并利用数值优化算法来实现的。这个过程不仅涉及复杂的数学理论，还需要编程实现和数值计算技巧。接下来的章节将深入到工具箱的实际使用中，通过具体代码示例，进一步讲解如何在实践中应用这些理论。

4. 工具箱核心功能详细说明

4.1 训练模型能力

4.1.1 模型训练参数设置

在使用Matlab LS-SVM1.5工具箱进行最小二乘支持向量机（LS-SVM）模型训练时，参数设置是一个关键步骤，它直接关系到模型的性能和泛化能力。模型训练的参数包括但不限于惩罚参数C、核函数类型和参数、以及优化算法的选择。

在Matlab环境下，我们可以通过函数调用的方式来设定这些参数。例如，使用 lssvm 函数进行模型训练时，可以指定 C 和核函数相关参数，如下所示：

% 假设X为特征矩阵，y为目标向量
model = lssvm(X, y, 'RBF', [1 100], 'options', optstruct);

在上述代码中， 'RBF' 表示使用高斯径向基函数（RBF）作为核函数， [1 100] 为RBF核的参数γ的范围。 optstruct 是一个结构体，包含了优化算法的设置。

4.1.2 核函数的选择与配置

在LS-SVM模型中，核函数用于将原始数据映射到高维空间，以便在该空间中求解线性可分问题。正确选择核函数对于模型性能至关重要。LS-SVM工具箱支持多种核函数，如多项式核、高斯径向基函数（RBF）核等。

选择合适的核函数通常需要根据具体问题的性质来决定。例如，对于非线性可分的数据，RBF核通常是一个不错的选择，因为它可以将数据映射到无限维空间，从而更容易找到最优的决策边界。

核函数的配置示例代码如下：

% 设定RBF核函数及其参数
kernelFunction = 'RBF';
kernelParams = [1 100]; % γ 和 σ 的值

% 配置LS-SVM模型训练时核函数参数
model = lssvm(X, y, kernelFunction, kernelParams);

在上述代码中， kernelFunction 指定了使用RBF核， kernelParams 为RBF核的参数。这些参数需要根据具体问题进行调整，以获得最佳的模型性能。

4.2 调参优化方法

4.2.1 参数选择的重要性

在LS-SVM模型训练过程中，参数选择是影响模型性能的关键因素之一。主要参数包括正则化参数C、核函数参数（如RBF核的γ），以及优化算法中的其他参数。参数选择不当可能导致过拟合或欠拟合，影响模型的泛化能力。

为了找到最佳的参数组合，通常需要进行参数优化或调参。调参过程涉及到参数的搜索空间定义、搜索策略选择以及性能评估标准的设定。常用的方法包括网格搜索（Grid Search）、随机搜索（Random Search）、贝叶斯优化等。

4.2.2 自动调参技术与策略

自动调参技术是指自动化地选择模型参数的过程，旨在减少人工干预，提高模型训练的效率和效果。在Matlab LS-SVM1.5工具箱中，可以使用内置的自动调参功能，如 lssvmcv 函数，来实现交叉验证和参数选择。

自动调参策略的实现通常涉及到多步骤，以网格搜索为例：

1. 参数空间定义 ：定义C和核函数参数的范围以及搜索步长。
2. 性能评估 ：使用交叉验证来评估给定参数组合下的模型性能。
3. 选择最佳参数 ：从所有可能的参数组合中选择一个最佳的组合，使得交叉验证的平均性能最好。

以下是自动调参的代码示例：

% 使用网格搜索进行交叉验证和参数优化
model = lssvmcv(X, y, 'RBF', [1 100], 10); % 10折交叉验证

在上述代码中， 'RBF' 是核函数类型， [1 100] 是核函数参数的搜索范围， 10 是交叉验证的折数。通过 lssvmcv 函数，工具箱自动搜索最佳的C和RBF参数。

4.3 预测与评估机制

4.3.1 模型预测方法与流程

在LS-SVM模型训练完成后，模型可以用来对新的数据样本进行预测。模型预测的过程通常简单直接，只需要将模型和新数据作为输入即可。在Matlab中，可以使用 predict 函数来进行预测。

下面是一个使用训练好的模型进行预测的示例：

% 假设model为训练好的LS-SVM模型，X_new为新的特征矩阵
predictions = predict(model, X_new);

在上述代码中， X_new 包含需要进行预测的新数据样本。 predictions 变量将包含模型对这些新样本的预测结果。

4.3.2 评估指标与模型验证

模型评估是确保模型具有良好的泛化能力的重要步骤。常用的评估指标包括准确率（Accuracy）、精确度（Precision）、召回率（Recall）、F1分数（F1 Score）等。此外，混淆矩阵（Confusion Matrix）也是常用的评估方法之一。

在Matlab中，评估模型性能可以使用 confusionmat 和 accuracy 等函数来计算评估指标。下面是一个使用混淆矩阵和计算准确率的示例：

% 假设y_true为真实标签，y_pred为模型预测结果
cm = confusionmat(y_true, y_pred);
accuracy = sum(diag(cm)) / sum(cm(:));

% 可以进一步计算其他评估指标
precision = cm(1,1)/(cm(1,1) + cm(1,2));
recall = cm(1,1)/(cm(1,1) + cm(2,1));
F1_score = 2 * (precision * recall) / (precision + recall);

在上述代码中， confusionmat 函数计算混淆矩阵，而 sum(diag(cm)) 计算对角线元素之和，代表正确预测的数量。除以 sum(cm(:)) 得到准确率。同样的方法可以计算精确度、召回率和F1分数。

4.4 可视化数据与模型决策边界

4.4.1 数据可视化工具与方法

数据可视化是理解和分析数据的重要手段，Matlab提供了多种强大的工具和函数用于可视化。例如， scatter 函数可以用来绘制散点图， plot 函数可以绘制线图等。

对于LS-SVM模型，可视化主要涉及到决策边界和数据点的展示。在Matlab中，可以将模型预测结果和实际数据结合使用 scatter 和 contour 等函数来进行可视化：

% 假设X为二维特征空间的数据点
figure;
scatter(X(:,1), X(:,2), 50, y_pred, 'filled');
hold on;

% 绘制决策边界
[x_min, x_max] = xlim;
[y_min, y_max] = ylim;
[Xi, Yi] = meshgrid(x_min:x_max, y_min:y_max);
Z = predict(model, [Xi(:), Yi(:)]);
Z = reshape(Z, size(Xi, 1), size(Xi, 2));
contour(Xi, Yi, Z, [-1 0 1], 'k');
hold off;

在上述代码中， scatter 函数用于绘制数据点，并根据 y_pred 的值用不同颜色区分。 contour 函数用于绘制决策边界，其中 Z 是模型在网格点上的预测值， [-1 0 1] 是决策边界的等高线值。

4.4.2 决策边界可视化技术

在机器学习中，可视化决策边界是一个直观展示模型学习结果的方法。对于LS-SVM模型，决策边界的可视化尤其重要，因为它可以帮助我们理解模型是如何在特征空间中划分数据的。

以下是一个使用Matlab进行LS-SVM决策边界可视化的完整流程：

% 绘制数据点
figure;
scatter(X(:,1), X(:,2), 50, y, 'filled');
hold on;

% 创建网格以进行插值
[x_min, x_max] = xlim;
[y_min, y_max] = ylim;
[Xi, Yi] = meshgrid(x_min:x_max, y_min:y_max);

% 预测网格上的值
Z = predict(model, [Xi(:), Yi(:)]);
Z = reshape(Z, size(Xi, 1), size(Xi, 2));

% 绘制决策边界
contour(Xi, Yi, Z, [0, 0], 'k', 'LineWidth', 2);
% 绘制支持向量
sv = model.sv;
plot(sv(:,1), sv(:,2), 'ko', 'MarkerSize', 10, 'MarkerFaceColor', 'y');

hold off;

在上述代码中， contour 函数绘制了决策边界，并通过 [0, 0] 参数指定了等高线的值，以便清晰地展示决策区域。支持向量的绘制通过 plot 函数完成，使用了不同的标记和颜色来突出显示。

4.5 应用示例和文档支持

4.5.1 实际应用案例分析

LS-SVM工具箱在实际问题中的应用广泛，包括但不限于生物信息学、金融风险预测、图像处理等领域。以下是一个在生物信息学中应用LS-SVM进行分类的实际案例分析。

假设我们有一组基因表达数据，目标是根据这些数据预测样本的分类标签（如正常与异常样本）。使用LS-SVM模型的流程可以分为以下几个步骤：

1. 数据预处理 ：标准化基因表达数据，以消除不同量纲的影响。
2. 模型训练 ：使用训练数据集来训练LS-SVM模型。
3. 模型验证 ：使用交叉验证来评估模型的泛化能力。
4. 应用模型 ：将训练好的模型应用于测试数据集，进行样本分类。

4.5.2 工具箱文档与帮助资源

Matlab LS-SVM1.5工具箱提供了详尽的文档和帮助资源，这些资源对于理解工具箱的功能和正确使用工具箱至关重要。文档通常包括：

• 安装说明 ：提供工具箱的安装流程。
• 函数参考 ：详述了所有可用的函数及其参数。
• 示例脚本 ：包含了一系列示例脚本，演示如何使用工具箱进行各种任务。
• 常见问题解答（FAQ） ：针对常见问题提供了快速解答。

在Matlab的帮助浏览器中，可以搜索特定的函数或关键词来快速访问这些文档资源。例如，输入 help lssvm 将提供关于 lssvm 函数的详细文档，包括参数说明、使用示例以及可能的输出结果等。

通过这些文档和资源，用户可以更有效地学习和使用Matlab LS-SVM1.5工具箱，解决各种机器学习问题。

5. 数据预处理和模型结果解释

5.1 数据预处理的重要性

在机器学习领域，数据预处理是构建准确模型的一个至关重要的步骤。数据预处理包括多个方面，从数据清洗到特征提取，再到数据标准化与归一化等。这些步骤共同作用，旨在提高数据质量和模型性能。

5.1.1 数据清洗与特征提取

数据清洗是预处理过程中的第一步，旨在识别并移除数据集中的噪声和异常值。噪声指的是数据集中的随机误差或错误，而异常值通常是指那些与数据集中的其他数据相差很大的点。在LS-SVM模型中，处理噪声和异常值有助于提高模型的泛化能力。

在特征提取方面，数据预处理包括了降维技术，如主成分分析（PCA）以及特征选择等方法。这些方法有助于去除不相关的特征，从而减少模型训练时间，并提高模型的准确度和解释能力。在使用Matlab LS-SVM工具箱时，我们可以利用内置的PCA功能来减少特征空间的维度，提高模型效率。

% 示例代码：数据清洗与特征提取
% 假设 X 是原始特征数据矩阵，Y 是对应的标签向量

% 数据清洗示例：移除包含缺失值的样本
clean_idx = ~any(isnan(X), 2);
X_clean = X(clean_idx, :);
Y_clean = Y(clean_idx);

% 特征提取示例：使用PCA降维
pca = fitpca(X_clean);
X_pca = predict(pca, X_clean);

% 显示降维后的数据
disp(X_pca);

5.1.2 数据标准化与归一化方法

数据标准化和归一化是确保不同特征在同一量级上进行比较的有效方法。标准化通常将数据转换为均值为0，方差为1的分布，而归一化则将数据缩放到一个特定的范围，例如[0,1]。

在使用LS-SVM时，特别是涉及到核函数的场景中，对数据进行标准化或归一化处理是十分必要的。这有助于加速模型的收敛速度，以及改善优化算法的性能。

% 示例代码：数据标准化与归一化
% 假设 X 是需要标准化的数据矩阵

% 数据标准化
X_std = zscore(X);
% 数据归一化到[0,1]
X_minmax = (X - min(X)) ./ (max(X) - min(X));

% 显示标准化和归一化后的数据
disp(X_std);
disp(X_minmax);

5.2 模型结果的解释与分析

在数据预处理完成后，我们可以用LS-SVM工具箱进行模型训练。但更重要的是，我们需要对模型结果进行解释和分析，以确保模型的预测结果是可信的，并且我们可以从中学到一些有意义的规律。

5.2.1 解释模型参数的意义

LS-SVM模型参数通常包括了支持向量、核函数参数以及正则化参数等。理解这些参数的含义对于解释模型结果至关重要。

• 支持向量 ：LS-SVM模型中的支持向量是决定模型决策边界的那些数据点。它们是数据集中的关键样本，了解这些样本的特征有助于我们理解模型的决策逻辑。
• 核函数参数 ：核函数的参数（比如高斯核的带宽参数σ）决定了模型处理非线性问题的能力。核函数的选择和参数的设置直接影响到模型在高维空间的性能。
• 正则化参数 ：正则化参数λ是控制模型复杂度和过拟合风险的关键，过大的λ会导致欠拟合，而过小的λ则可能引起过拟合。

5.2.2 模型结果的可信度评估

评估模型结果的可信度包括了对模型预测准确性的验证和对模型泛化能力的测试。通常使用交叉验证的方法，如k折交叉验证，来评估模型对未知数据的预测能力。

% 示例代码：交叉验证与模型准确性评估
% 假设 X_train 和 Y_train 是训练集，X_test 和 Y_test 是测试集
% 假设 SVM_model 是已训练好的LS-SVM模型

% 进行k折交叉验证
k = 5;
cv = crossval(SVM_model, X_train, Y_train, 'KFold', k);

% 计算交叉验证的平均准确率
accuracy = kfoldLoss(cv);

% 使用测试集进行模型评估
predictions = predict(SVM_model, X_test);
accuracy_test = sum(predictions == Y_test) / numel(Y_test);

% 显示模型的准确性
fprintf('交叉验证准确率：%.2f%%\n', accuracy * 100);
fprintf('测试集准确率：%.2f%%\n', accuracy_test * 100);

通过这些步骤，我们不仅可以量化模型的性能，还可以通过分析模型的预测结果，对模型的决策逻辑有更深入的理解。这样的分析是后续优化模型和改进预测方法的基础。

graph TD
A[开始] --> B[数据预处理]
B --> C[模型训练]
C --> D[交叉验证]
D --> E[模型评估]
E --> F[模型优化]
F --> G[结束]

通过上述章节的介绍，我们已经详细学习了LS-SVM模型在数据预处理和模型结果解释方面的应用和重要性。这为在后续章节中深入探讨模型的优化和实际应用提供了坚实的基础。

6. 工具箱在实际工程问题中的应用

随着人工智能和机器学习技术的飞速发展，最小二乘支持向量机（Least Squares Support Vector Machine，简称LS-SVM）已成为数据科学领域解决分类和回归问题的重要工具。在工业界，LS-SVM工具箱的应用越来越广泛，其在不同工程问题中的应用细节、解决策略及成功案例，都成为了从业者们关注的焦点。本章节将详细介绍工具箱在实际工程问题中的应用，包括工程问题的分类与处理，以及成功案例与经验分享。

6.1 工程问题的分类与处理

工程问题广泛涉及到各种实际应用场景，例如制造业的质量控制、金融领域的风险评估、医疗行业的疾病诊断等。这些问题往往数据量庞大且特征众多，给模型的训练和预测带来了不小的挑战。应用LS-SVM工具箱可以有效地解决此类问题，具体步骤如下：

6.1.1 不同类型工程问题的特点

工程问题通常分为分类问题和回归问题。分类问题的目标是将数据分为特定的类别，例如判断邮件是否为垃圾邮件；回归问题则预测一个连续的输出值，例如股票价格的预测。每种问题类型都需要选择合适的LS-SVM模型配置来处理。

6.1.2 工具箱应用的适配与调整

在应用LS-SVM工具箱时，首先需要对问题进行分析，根据问题的特点选择合适的核函数。例如，在非线性问题中，可以选择高斯径向基函数（RBF）核。其次，需要调整模型的超参数，如正则化参数和核函数参数，以达到最佳的训练效果。

6.2 成功案例与经验分享

为了更好地理解LS-SVM工具箱在实际工程问题中的应用，本节将通过两个成功案例进行分析，并分享在应用过程中的经验与教训。

6.2.1 典型案例的分析与总结

案例一：制造业质量控制

在一个制造业的质量控制问题中，利用LS-SVM工具箱构建了一个质量预测模型。通过应用多种核函数进行尝试，发现RBF核能够更好地捕捉数据之间的复杂关系。通过多次交叉验证选择最佳的超参数组合，模型在测试集上达到了较高的准确率。

案例二：金融风险评估

在金融风险评估问题中，使用LS-SVM工具箱建立了一个信用评分模型。为了提高模型的泛化能力，除了RBF核之外，还尝试了多项式核和线性核。通过参数优化和特征选择，模型不仅提高了预测精度，还缩短了预测时间。

6.2.2 应用工具箱的经验与教训

在使用LS-SVM工具箱的实践中，我们积累了以下几点经验：

1. 数据预处理 ：数据的质量直接决定了模型的性能。在应用工具箱之前，应当进行彻底的数据清洗和预处理，这包括去除噪声、处理缺失值和异常值。

2. 核函数的选择 ：合适的核函数能够显著提高模型的性能。在实际应用中，我们发现RBF核往往表现更好，但也需要尝试其他核函数，如多项式核，来确定最适合问题的核函数。

3. 超参数的调整 ：超参数的选择对模型性能有重大影响。通过网格搜索、随机搜索或贝叶斯优化等方法进行超参数优化，有助于找到最佳的参数组合。

4. 模型的解释性 ：尽管LS-SVM是一个强大的模型，但其解释性相对较差。在某些领域，如医疗诊断，模型的可解释性是一个关键因素。因此，我们需要在模型性能和可解释性之间找到平衡。

5. 性能评估 ：模型评估不应仅仅依赖于准确性。在分类问题中，混淆矩阵、精确率、召回率和F1分数等指标提供了更全面的性能视图。在回归问题中，均方误差（MSE）、均方根误差（RMSE）和决定系数（R²）等指标是重要的评估标准。

6. 模型的持续更新 ：随着新数据的不断积累，模型性能可能会下降。定期重新训练模型，或者引入在线学习机制，保持模型的时效性是持续应用中的重要环节。

通过这些案例和经验的分享，可以看到LS-SVM工具箱在实际工程问题中具有广泛的应用潜力，并且随着正确的配置和应用，可以取得很好的效果。工具箱的应用并非一成不变，而是需要根据实际问题的特点进行适当的调整和优化。

在下一章中，我们将进一步探讨数据预处理和模型结果的解释与分析，深入理解模型参数的意义和模型结果的可信度评估。这将帮助我们更好地掌握LS-SVM工具箱的使用，并在实际应用中取得更好的效果。

7. LS-SVM模型的高级优化与改进策略

7.1 面临的常见问题与挑战

在实际应用中，LS-SVM模型的性能受到多种因素的影响，包括数据集的质量、参数选择、计算资源等。一些常见的问题包括过拟合、欠拟合、参数优化困难以及大规模数据处理效率低下等。为了克服这些挑战，需要对LS-SVM进行一些高级优化和改进。

7.2 高级参数优化技术

为了提高LS-SVM的性能，高级参数优化技术是不可或缺的。下面介绍两种常用的高级参数优化技术：网格搜索和随机搜索。

7.2.1 网格搜索

网格搜索是一种穷举搜索方法，通过遍历所有可能的参数组合来寻找最优解。这种方法虽然计算量大，但能保证找到全局最优解。其步骤如下：

• 确定需要优化的参数及其可能的取值范围。
• 在参数范围内均匀地选择一系列值，形成参数网格。
• 对每个参数组合使用交叉验证进行性能评估。
• 选择性能最优的参数组合作为最终模型的参数。

网格搜索的代码实现如下：

from sklearn.model_selection import GridSearchCV
from sklearn.svm import LinearSVC

# 假设X_train, y_train为训练数据集
parameters = {'C': [1, 10, 100, 1000], 'loss': ['squared_hinge', 'hinge']}
svc = LinearSVC()
clf = GridSearchCV(svc, parameters, cv=5)
clf.fit(X_train, y_train)

print("最优参数: {}".format(clf.best_params_))

7.2.2 随机搜索

随机搜索是一种基于随机采样的优化方法，其搜索过程更为高效，尤其是在参数空间很大时。它的基本思想是在预定义的参数分布中随机选择参数组合进行搜索。以下是随机搜索的一个实例：

• 指定参数的概率分布。
• 根据分布随机选择参数值，而不是遍历所有可能值。
• 类似网格搜索，使用交叉验证评估每个参数组合。
• 选择性能最优的参数组合。

随机搜索的代码示例如下：

from sklearn.model_selection import RandomizedSearchCV
import numpy as np

# 假设X_train, y_train为训练数据集
parameters = {'C': np.logspace(-4, 4, 20), 'loss': ['squared_hinge', 'hinge']}
svc = LinearSVC()
clf = RandomizedSearchCV(svc, parameters, n_iter=10, cv=5)
clf.fit(X_train, y_train)

print("最优参数: {}".format(clf.best_params_))

7.3 提升LS-SVM计算效率的策略

面对大规模数据集时，计算效率成为一个重要问题。以下是一些提升LS-SVM计算效率的策略：

7.3.1 核函数选择

在选择核函数时，应优先考虑计算复杂度较低的核函数，例如线性核和多项式核。高斯核虽然适用性广泛，但其计算成本高，不适用于大规模数据集。

7.3.2 稀疏数据优化

对于稀疏数据集，可以使用特殊的稀疏优化算法，如序列最小优化（SMO）算法，以减少计算资源消耗。

7.3.3 数据缩减技术

对于特别大的数据集，可以使用数据缩减技术，如主成分分析（PCA），来降低数据的维度，从而加速模型训练。

7.3.4 并行计算

利用现代计算机的多核处理器能力，通过并行计算可以显著提高训练速度。一些开源的LS-SVM实现已经支持并行计算。

7.4 改进策略的实践操作

在本节中，将通过一个简单示例，展示如何在Python中使用LS-SVM模型，并应用上述提到的改进策略来优化模型性能。

实践步骤：

1. 导入必要的库和数据集。
2. 选择合适的核函数和参数。
3. 应用网格搜索或随机搜索进行参数优化。
4. 使用选取的最优参数构建LS-SVM模型。
5. 评估模型的性能。

以下是实现这些步骤的伪代码示例：

# 导入库和数据
from sklearn import datasets
from sklearn.svm import LinearSVC
from sklearn.model_selection import GridSearchCV

# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 设置模型和参数范围
model = LinearSVC()
parameters = {'C': [0.1, 1, 10, 100]}

# 使用网格搜索优化参数
clf = GridSearchCV(model, parameters, cv=5)
clf.fit(X, y)

# 选取最优参数
best_params = clf.best_params_
best_model = clf.best_estimator_

# 模型评估
from sklearn.metrics import accuracy_score
predictions = best_model.predict(X)
print("模型准确率: {:.2f}%".format(accuracy_score(y, predictions) * 100))

通过这样的实践操作，可以实现LS-SVM模型在特定问题上的性能提升。在实际应用中，还应结合数据集特性和问题背景，灵活调整上述策略。

本文还有配套的精品资源，点击获取

简介：LS-SVM是一种用于非线性分类和回归问题的机器学习模型，Matlab的LS-SVM1.5工具箱让研究人员和工程师能方便地在Matlab环境中实现该算法。工具箱通过最小化平方误差构建决策边界，可能在处理过拟合时表现更佳。其主要功能包括模型训练、参数优化、预测与评估、数据可视化、应用示例以及文档支持。对于初学者而言，附带的示例脚本和详尽文档是非常有帮助的资源。掌握LS-SVM工具箱，用户可以解决多种实际工程问题。

本文还有配套的精品资源，点击获取