回归分析预测法例题_基于层次回归法的调节作用分析实操

理论背景

如果因变量Y和自变量X的关系（回归斜率的大小和方向）随第三个变量M的变化而变化，则称M在X和Y之间起调节作用，此时称M为调节变量（见下图）。

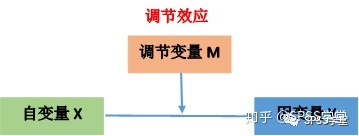
当使用SPSS进行调节效应分析的时，分析方法会因自变量和调节变量是连续还是分类变量而有所区别。本篇文章针对的是自变量是连续变量、调节变量是分类变量这种情况。

我们先梳理一下在SPSS里使用回归法进行此情况分析的思路：比较两个回归方程Y = i+ aX + bM+c 和Y = i+ aX + bM +cXM +c（多了交互项XM）这两个回归方程是否有显著差异。因为调节变量是分类变量，所以我们需要对调节变量进行虚拟编码，所以最终，交互项XM实际上可能不止一项。这里调节效应的检验，其实质也是层次回归的方法。

1 虚拟变量( Dummy Variables)：取值为0或1的人工变量，其作用是实现对分类变量的量化、反映变量质的属性，又称虚设变量、名义变量或哑变量。

虚拟变量设置规则：

1 “0”和“1”选取原则：所有的虚拟变量，取值只有0或1两种；

2 虚拟变量个数：如果变量X有N个水平，在有截距项的模型中，可以用N-1个虚拟变量来表示这个变量X；

虚拟变量举例：

某一年级变量X包含大一、大二、大三、大四四个水平，我们将大一作为比较变量，使用三个虚拟变量编码这个年级变量X。如下表所示，第一列是年级变量X的四个水平，第一行是三个虚拟变量。这样，三个虚拟变量就可以分别编码变量X的每个水平了。

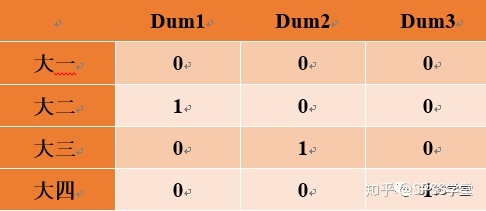
步骤解析

1 对调节变量M进行虚拟编码，产生虚拟变量。

2 产生自变量X与虚拟变量的相乘交互项。

3 用自变量X、虚拟变量对因变量Y做回归。

4 用自变量X、虚拟变量、相乘交互项对因变量Y做回归。

5 观察结果判断调节效应是否成立。

实际操作

1.1 打开数据文件，有三个变量：自变量X（连续变量）、拟调节变量M（分类变量，四个水平）、因变量Y（连续变量）。

1.2 在spss里将拟调节变量进行虚拟编码。【转换】——【创建虚变量】。

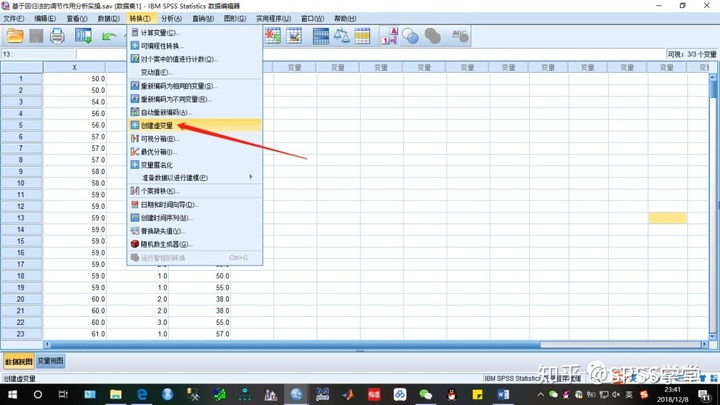
1.3 第一步在【针对下列变量创建虚变量（C）】中导入变量M。第二步给虚变量命名，如下图所示，这里我们将其命名为Mdum，点击【确定】即可。

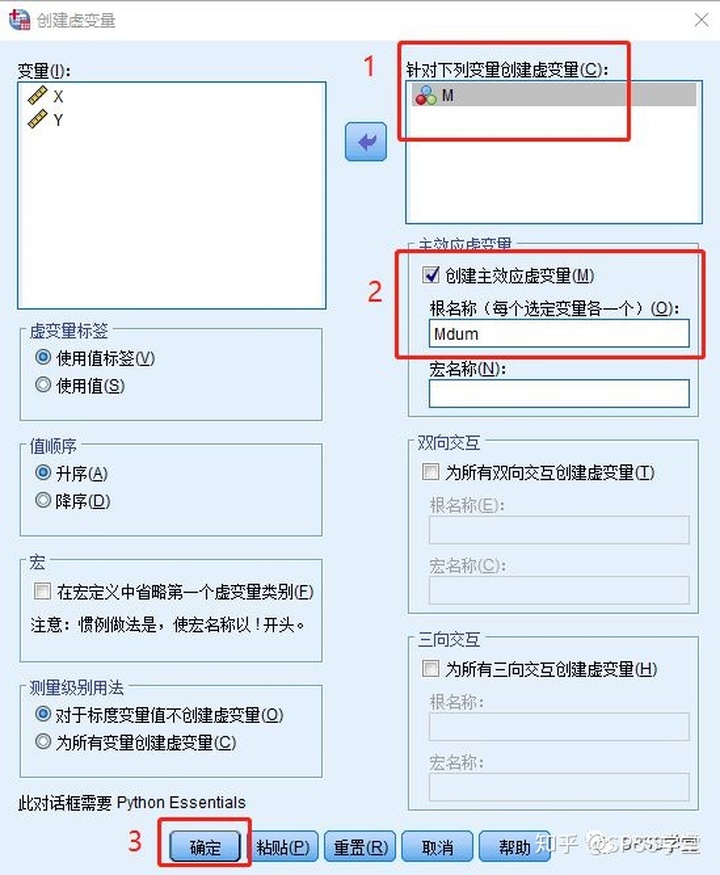
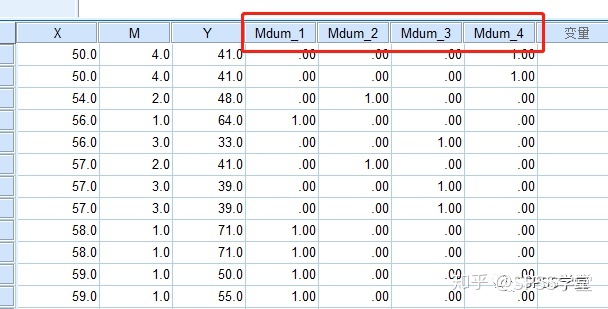
1.4 生成四个虚拟变量Mdum_1、Mdum_2、Mdum_3、Mdum_4，我们只需要三个虚拟变量即可完成对变量M的编码，因此我们可以选择删除其中一个。若将M=4.0作为对照的变量水平，这里可以选择删除Mdum_4。选中这一列，右键【清除】。

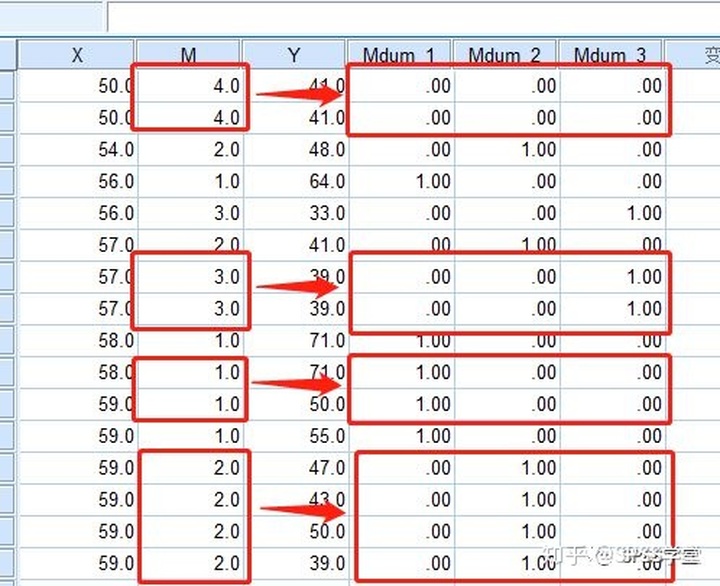
1.5 这样，虚拟变量便准备好了。可以看到，当M=4.0，三个虚拟变量的值分别为0 0 0，当M=3.0，三个虚拟变量的值分别为0 0 1，当M=1.0，三个虚拟变量的值分别为1 0 0，当M=2.0，三个虚拟变量的值分别为0 1 0。

2.1 产生自变量X与虚拟变量的相乘交互项。【转换】——【计算变量】。我们要将三个虚拟变量分别与X相乘，所以将会产生三个新的相乘交互项。

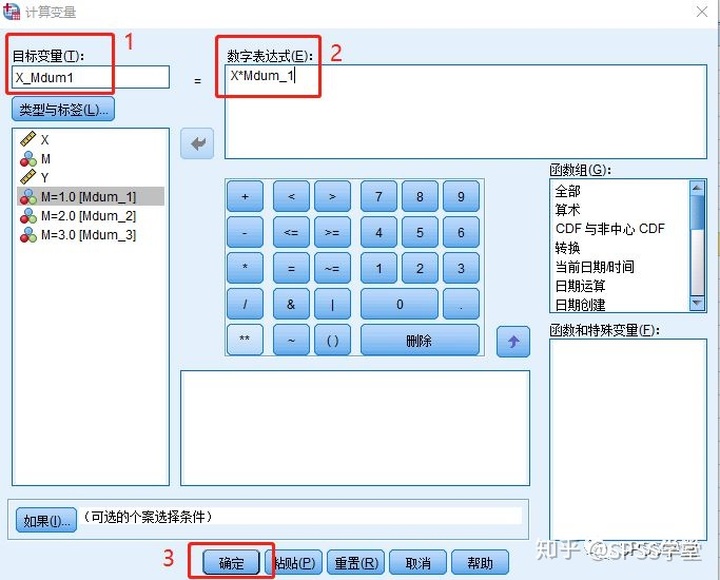
2.2 产生第一个相乘交互项。第一步，在【目标变量（T）】中输入，给这新的变量起个变量名。在【数字表达式（E）】中，令X与Mdum_1相乘即可，点击【确定】。

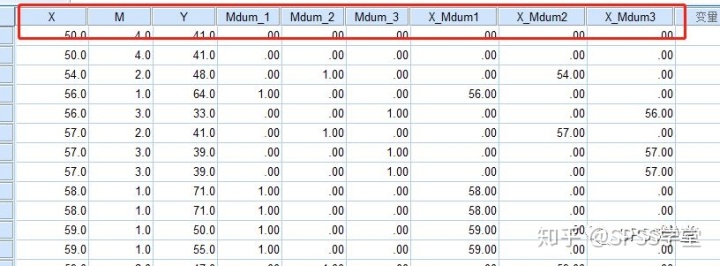
2.3 同样的步骤，令自变量分别与另外两个虚拟变量相乘，得到另外两个相乘交互项。由此，我们就有了下列这些变量。X、M、Y是我们原本就有的变量，期望得到他们的调节效应；Mdum_1、Mdum_2、Mdum_3是新产生的虚拟变量，用来编码变量M的四个水平；X_Mdum1、X_Mdum2、X_Mdum3是新产生的变量，由自变量X分别与三个虚拟变量相乘而来。

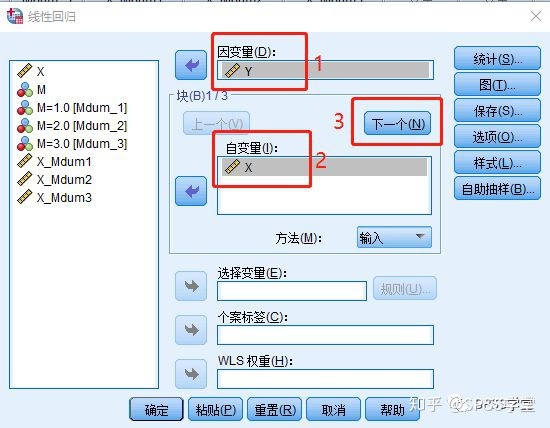
3.1 进行层次回归。点击【分析】——【回归】——【线性】，得到下图。我们需要做三层回归。第一层：【因变量（D）】中导入Y、【自变量（I）】中导入X，点击【下一个】，可以进入下一层。

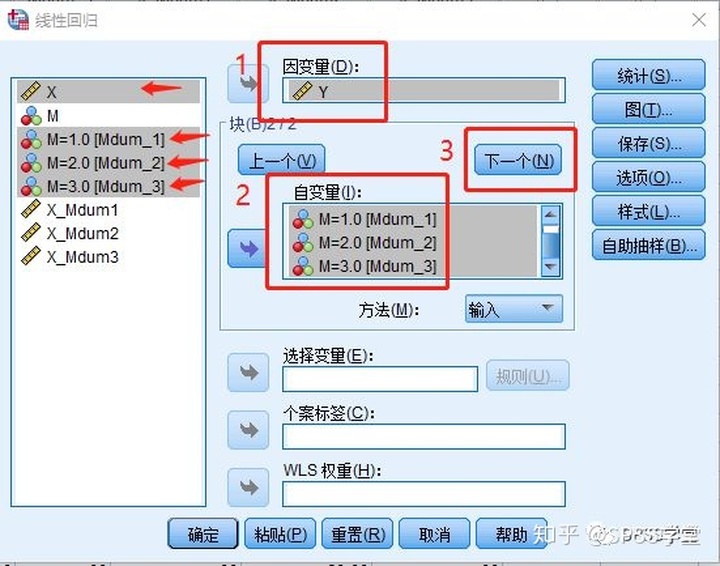
3.2 第二层：【因变量（D）】中导入Y、【自变量（I）】中导入X、Mdum_1、Mdum_2、Mdum_3，点击【下一个】，可以进入下一层。

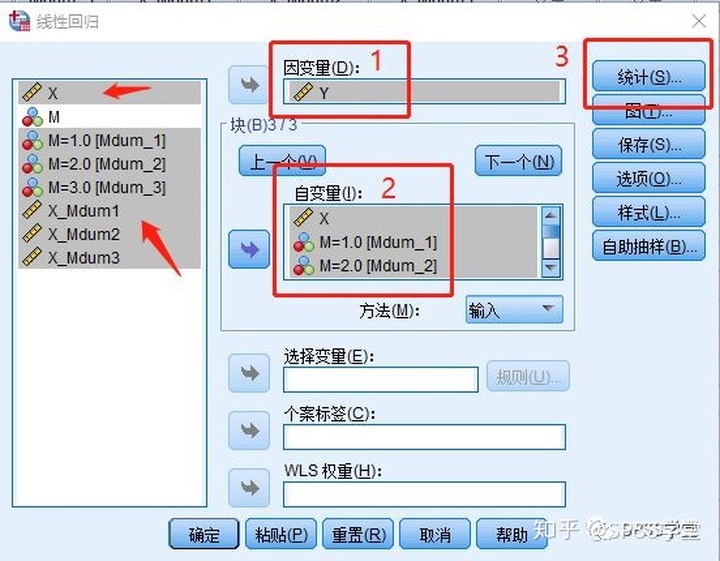
3.3 第三层：【因变量（D）】中导入Y、【自变量（I）】中导入X、Mdum_1、Mdum_2、Mdum_3、X_Mdum1、X_Mdum2、X_Mdum3。三层回归准备好以后，点击【统计】。

3.4 勾选【R方变化量】，并点击【继续】。回到主界面后，点击【确定】即可。

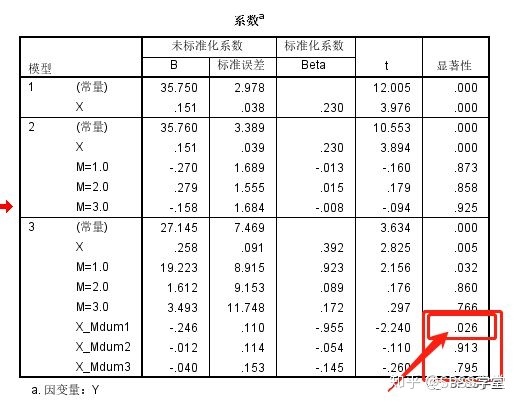
3.5 观察输出的结果。在第三层回归中，关注三个相乘交互项的系数显著性，可以发现，交互项X_Mdum1的系数显著，说明M的第一个水平，M=1.0在X与Y中间所起到的作用是不同于M的其他三个取值的。也就是因变量Y和自变量X的关系会随第三个变量M的变化而变化。由此可知，变量M的调节效应显著，主要体现在M=1.0和其他情况的区别。