catia圆角交点如何标注_Catia绘制直齿锥齿轮

第一步：启动

第二步：更改设置

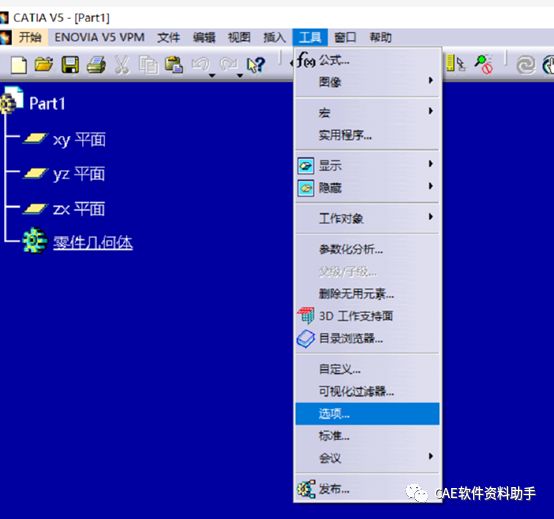
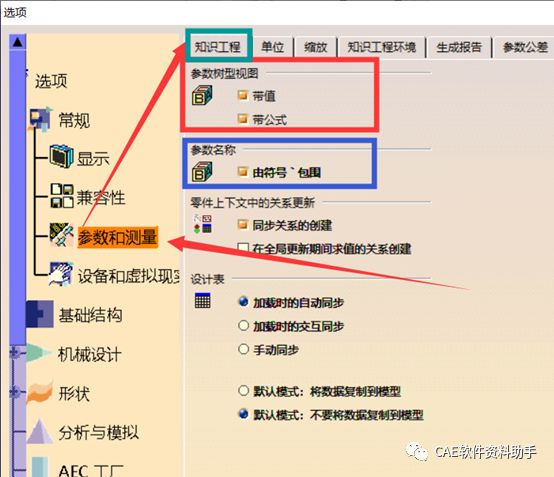
选择参数和测量->知识工程

一定要勾选参数树形视图下的值与公式两个选项，否则后面绘制参数型曲线时，极其的不方便。

参数名称由单引号包围可选可不选，为了方便辨识参数，勾选

以下蓝色小字是已知的。

锥齿轮的当量齿数Zv与两个因素相关，①齿轮齿数Z；②分度圆锥角δ。

与斜齿轮类似，但是锥齿轮的背锥是可以近似展开分析的。(锥齿轮的渐开线是球面渐开线，详情请参考相关文献，这里我暂时将其作为锥面分析，是为了后面可以展开成圆柱齿轮，从而方便计算。)

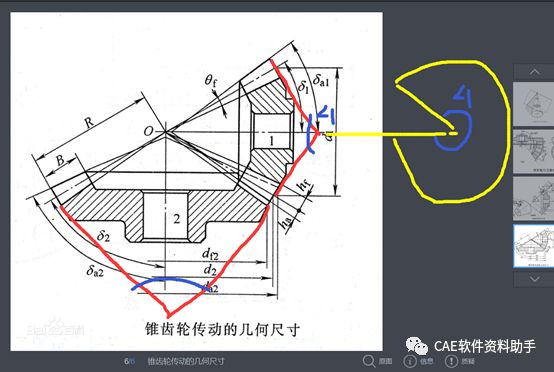
如图所示(图片来源于百度)，一对啮合的锥齿轮，将小齿轮的背锥面展开处理，注意小齿轮的蓝色的标注∠1的那个角度，在小齿轮上标注出来是空间角。然后黄色的是它的展开。

那么展开的扇形在它的圆弧部分上分布着齿，这些齿所构成的部分齿轮，，除了不完整以外，所有的参数和小锥齿轮的大端参数相同。

锥齿轮的几何参数计算是在大端面上进行的，所以像上面那样展开，通过计算展开的齿轮来间接计算锥齿轮的几何参数是可行的。

这个展开的齿轮将它补成完整的齿轮后，称为当量齿轮。由此可见当量齿轮是一个参数等同于锥齿轮大端面的普通直齿圆柱齿轮。

从以上的几何关系就可以导出一个当量齿轮齿数与锥齿轮齿数的关系。

Zv=Z/cosδ

Zv：当量齿数

Z：锥齿轮齿数

δ：锥齿轮分度圆锥角(小齿轮和大齿轮的锥角可能不同，绘制时δ也是不同的)。

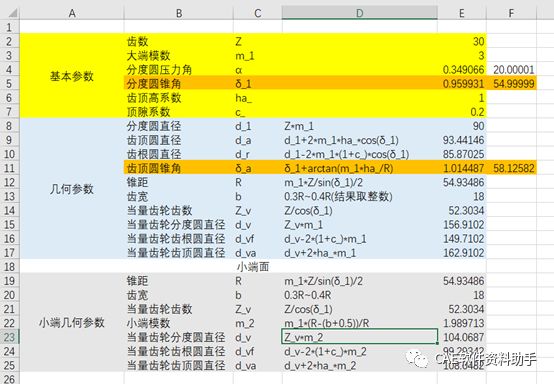
齿轮参数表：

建模思路:

先绘制一个齿坯，通过参数化建模绘制出大端面的渐开线，同理绘制小端面的渐开线，然后按照从大端面到小端面比例变化“刨”出齿轮的齿槽，最后阵列产生完整齿轮。