图的遍历
图的遍历目的是访问图的每一个顶点恰好一次,,同时访问图中每条边恰好一 次。
对于无向图,常见的遍历方式有深度优先遍历(Depth-First Search, DFS) 和广度优先遍历(Breadth-First Search, BFS)。
1 深度优先遍历(DFS)
深度优先遍历是一种用于遍历或搜索树或图的算法。
深度优先搜索是一个递归的过程。
- 首先,选定一个出发点后进行遍历,如果有邻接的未被访问过的节点则继续前进。
- 若不能继续前进,则回退一步再前进
- 若回退一步仍然不能前进,则连续回退至可以前进的位置为止。
- 重复此过程,直到所有与选定点相通的所有顶点都被遍历。
示例
先选择一个起始的顶点
、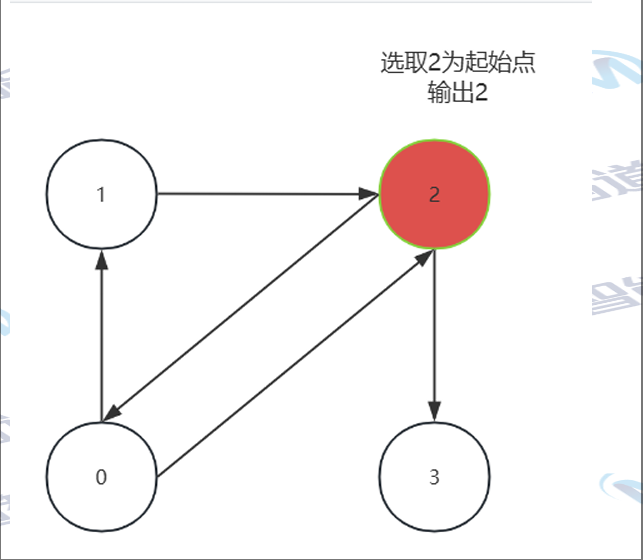
选择其中一个邻接点

3没有邻接点,回退到2

2有两个邻接点,但是3已经访问过了,选择0
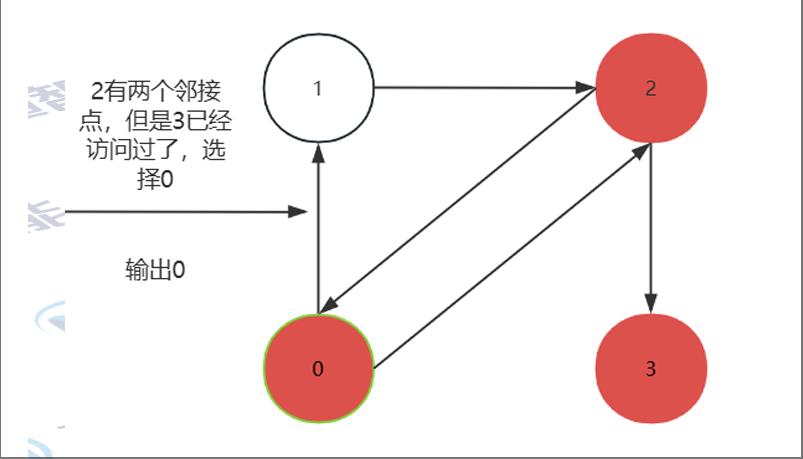
0有两个邻接点,但是2已经访问过了,选择1

1有1个邻接点,但是2已经访问过了,于是整个深度优先遍历完成,输出结果为2->3->0->1
代码如下:
#include <iostream>
using namespace std;
// 定义图的边(顶点值默认从0开始)用两个顶点之间的连接表示边
typedef struct Node
{
int vertex; // 下一个顶点的值
struct Node *next; // 下一条顶点(如果当前顶点没有更多的邻接点,则此指针为NULL)
} Node;
// 定义图
typedef struct Graph
{
int numVertices; // 顶点数
Node **adjLists; // 邻接表,指向指针数组的指针,每个指针都指向一个Node链表的头部。数组
// 的大小numVertices 数组元素则是指向从该顶点出发的第一条边的指针(如果顶点没有邻接点,则为
// NULL)。
bool *isVisited; // 标记看看是不是访问过 数组的大小numVertices (顶点数)
}Graph;
// 创建一个图,包含vertices个顶点
Graph *createGraph(int vertices)
{
Graph *graph = new Graph();
if (!graph)
{
perror("创建失败");
return nullptr;
}
// /初始化顶点数
graph->numVertices = 0;
graph->adjLists = new Node *[vertices]; // 表示一个包含 vertices 个 Node* 元素的数组。在C++中,数组名在大多数情况下会退化成指向数组首元素的指针
// new Node*[vertices] 返回的是一个指向包含 vertices 个 Node* 元素的数组的指针,其类型是 Node**,这与 adjLists 的类型匹配
// /为邻接表申请内存
for (int i = 0; i < vertices; ++i)
{
graph->adjLists[i] = nullptr;
}
// 标注位申请内存
graph->isVisited = new bool [vertices] { 0 };
return graph;
}
// 添加边 src起点 dest终点
void addEdge(Graph *graph, int src, int dest)
{
// 创建边
Node *newNode = new Node();
// //设置邻接点
newNode->vertex = dest;
// 将新边添加到起点的链表中
newNode->next = graph->adjLists[src];
// 更新第一天条边
graph->adjLists[src] = newNode;
graph->adjLists[src] = newNode;
如果是无向图,也需要添加反向边
Node* newNode2 = (Node*)malloc(sizeof(Node));
// Node* newNode2 = new Node;
// newNode2->vertex = src;
// newNode2->link = graph->adjLists[dest];
// graph->adjLists[dest] = newNode2;
}
// 深度优先遍历
void DFS(Graph *graph, int v)
{
// 输出遍历到的节点
cout << v << " ";
// 递归访问所有未访问的邻接顶点
Node *adjList = graph->adjLists[v];
while (adjList)
{
// 标记当前节点为已访问
graph->isVisited[v] = true;
// 邻接点未被访问到
if (!graph->isVisited[adjList->vertex])
{
// 递归调用 访问他的所有邻接点
DFS(graph, adjList->vertex);
}
// 往后遍历每一条边
adjList = adjList->next;
}
}
// 清理Graph对象
void freeGraph(Graph *graph)
{
if (!graph)
{
return;
}
// 释放邻接表中每个链表占用的内存
for (int i = 0; i < graph->numVertices; ++i)
{
Node *current = graph->adjLists[i];
while (current)
{
Node *next = current->next; // 保存下一条边的指针
delete current; // 释放当前边的内存
current = next; // 移动到下一条边
}
}
// 释放邻接表数组本身占用的内存
delete[] graph->adjLists;
// 释放访问标记数组占用的内存
delete[] graph->isVisited;
}
int main()
{
// 创建一个包含4个顶点的图
Graph *graph = createGraph(4);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 2, 0);
addEdge(graph, 2, 3);
// 深度优先遍历图
cout << "深度优先遍历(从顶点2开始):" << endl;
DFS(graph, 2);
delete graph;
graph = NULL;
return 0;
}
newNode1->next = graph->adjList[src];意思是 新节点的 next 指针指向当前 src 邻接链表的第一个节点。
这样,新节点 newNode1 被插入到链表的头部
graph->adjList[src] = newNode1; 将 src 的邻接链表的头部更新为 newNode1。这样,newNode1 成为链表的新头节点
结果是
深度优先遍历(从顶点2开始):
2 0 1 3
1.2 广度优先遍历(BFS)
广度优先遍历是图的另一种遍历方式,它从根节点开始,首先访问离根节点最近的节点(即根节点的所 有邻接节点),然后逐层向外访问,直到访问完所有节点。
- 从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点
- 然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。
- 如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止(队列为空)。
示例
先选择一个起始的顶点·

2的邻接点有两个,全部入队,队列元素为3, 0

3没有邻接点,出列,输出3,队列元素为0

0的邻接点是1和2,但是2已经访问过了,1入队,0出列,输出0,队列元素为1

1的邻接点是2,但是2已经访问过了,0出列,输出0,队列元素为空,同时访问完毕 整个广度优先遍历完成,输出结果为2->3->0->1

代码如下
#include <iostream>
using namespace std;
#include <queue>
// 定义图的边(顶点值默认从0开始)用两个顶点之间的连接表示边
typedef struct Node
{
int vertex; // 下一个顶点的值
struct Node *next; // 下一条顶点(如果当前顶点没有更多的邻接点,则此指针为NULL)
} Node;
// 定义图
typedef struct Graph
{
int numVertices; // 顶点数
Node **adjLists; // 邻接表,指向指针数组的指针,每个指针都指向一个Node链表的头部。数组
// 的大小numVertices 数组元素则是指向从该顶点出发的第一条边的指针(如果顶点没有邻接点,则为
// NULL)。
bool *isVisited; // 标记看看是不是访问过 数组的大小numVertices (顶点数)
}Graph;
// 创建一个图,包含vertices个顶点
Graph *createGraph(int vertices)
{
Graph *graph = new Graph();
if (!graph)
{
perror("创建失败");
return nullptr;
}
// /初始化顶点数
graph->numVertices = vertices;
graph->adjLists = new Node *[vertices]; // 表示一个包含 vertices 个 Node* 元素的数组。在C++中,数组名在大多数情况下会退化成指向数组首元素的指针
// new Node*[vertices] 返回的是一个指向包含 vertices 个 Node* 元素的数组的指针,其类型是 Node**,这与 adjLists 的类型匹配
// /为邻接表申请内存
for (int i = 0; i < vertices; ++i)
{
graph->adjLists[i] = nullptr;
}
// 标注位申请内存
graph->isVisited = new bool [vertices] { 0 };
return graph;
}
// 添加边 src起点 dest终点
void addEdge(Graph *graph, int src, int dest)
{
// 创建边
Node *newNode = new Node();
// //设置邻接点
newNode->vertex = dest;
// 将新边添加到起点的链表中
newNode->next = graph->adjLists[src];
// 更新第一天条边
graph->adjLists[src] = newNode;
如果是无向图,也需要添加反向边
Node* newNode2 = (Node*)malloc(sizeof(Node));
// Node* newNode2 = new Node;
// newNode2->vertex = src;
// newNode2->link = graph->adjLists[dest];
// graph->adjLists[dest] = newNode2;
}
// 深度优先遍历
void DFS(Graph *graph, int v)
{
// 输出遍历到的节点
cout << v << " ";
// 递归访问所有未访问的邻接顶点
// 第一个顶点
Node *adjList = graph->adjLists[v];
// 标记当前节点为已访问
graph->isVisited[v] = true;
while (adjList)
{
// 邻接点未被访问到
if (!graph->isVisited[adjList->vertex])
{
// 递归调用 访问他的所有邻接点
DFS(graph, adjList->vertex);
}
// 往后遍历每一条边
adjList = adjList->next;
}
}
// 广度优先遍历
void BFS(Graph* graph, int startVertex)
{
// 初始化队列
queue <int> q;
// / 标记所有顶点为未访问
for(int i = 0; i < graph->numVertices ; ++i)
{
graph->isVisited[i] = false;
}
// 将起始顶点加入队列,并标记为已访问
q.push(startVertex);
graph->isVisited[startVertex] = true;
// 循环条件是队列不为空
while (!q.empty())
{
// 从队列中取出第一个顶点
int vertex = q.front();
//出队
q.pop();
// 访问该顶点
cout << "Visited " << vertex << endl;
// 遍历访问的顶点的所有邻接点
Node* current = graph->adjLists[vertex];
while (current)
{
//邻接点 终点
int adjVertex = current->vertex;
// 如果邻接点未被访问,则加入队列并标记为已访问
if(!graph->isVisited[adjVertex])
{
q.push(adjVertex);
graph->isVisited[adjVertex] = true;
}
// 移动到下一个邻接点
current = current->next;
}
}
}
// 清理Graph对象
void freeGraph(Graph *graph)
{
if (!graph)
{
return;
}
// 释放邻接表中每个链表占用的内存
for (int i = 0; i < graph->numVertices; ++i)
{
Node *current = graph->adjLists[i];
while (current)
{
Node *next = current->next; // 保存下一条边的指针
delete current; // 释放当前边的内存
current = next; // 移动到下一条边
}
}
// 释放邻接表数组本身占用的内存
delete[] graph->adjLists;
// 释放访问标记数组占用的内存
delete[] graph->isVisited;
}
int main()
{
// 创建一个包含4个顶点的图
Graph *graph = createGraph(4);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 2, 3);
addEdge(graph, 2, 0);
// 深度优先遍历图
cout << "深度优先遍历(从顶点2开始):" << endl;
DFS(graph, 2);
cout << endl;
cout << "广度优先遍历(从顶点2开始):" << endl;
BFS(graph, 2);
delete graph;
graph = NULL;
return 0;
}
-
问题1:初始化的时候把顶点numVertices 初始化为0了而且创建时候没有再赋值,直接初始化传入节点就行了
-
问题2 graph->isVisited[v] = true; 放在循环外面,那么下面访问了之后会再标记吗
当然会,这是递归,会调用自己
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








