100以内偶数的个数_【数学杂谈】如何记住1000以内的所有质数？

绝大多数的同学都能熟练背诵一百以内的全部质数，然而一千以内的质数就并不一定可以背诵出来，这篇文章帮助大家用最简单的图像记忆法来记忆一百到一千之间的质数。

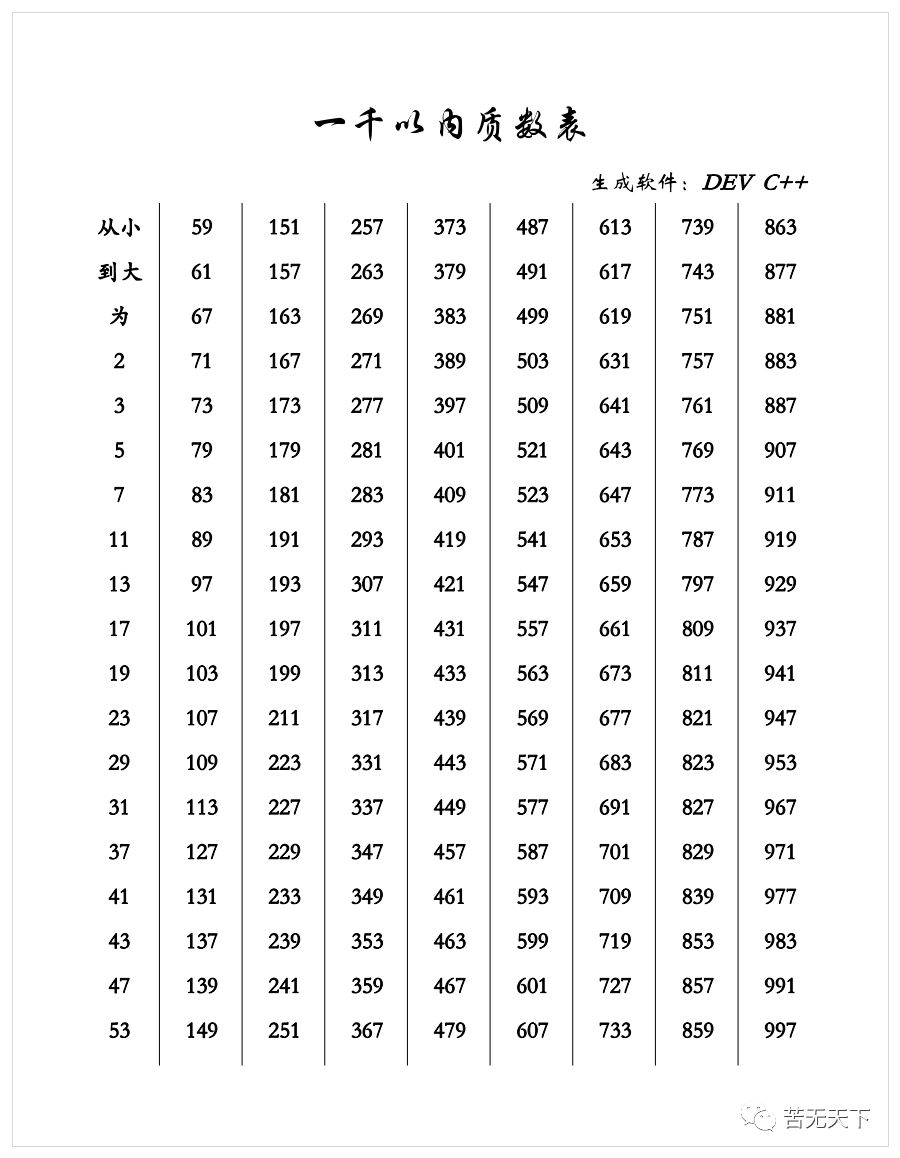
显而易见，任何大于2的偶数都不是质数、任何大于5的5的倍数都不是质数，如此一来我们只需要讨论末位数字为1、3、7、9的数是否是质数。

为了方便记忆，我们把100~1000分为9个板块，每100个数字为一个板块，而既然我们只需要研究末位数字为1、3、7、9的数，所以每个板块中我们只需要研究40个数。

为了直观地表现这40个数是否是质数，我们创建一个10行4列的表格，每个单元格代表一个数，如果这个数是质数，我们就把这个单元格涂黑。我们将涂色之后的成品图称为“质数分布图”。

例如，100~200的质数分布图如下：

这样一来，我们原本需要记忆的40个数字就变成了一张清晰的图片，而我们再分析就会发现：这张图分为了7个板块，其中3个板块是单独的单元格，4个板块有特定的形状特征，这样我们就只需要记忆这7个板块的位置所在。

但是，真的是7个吗？如果我们观察白色单元格，就会发现：仅仅只有5个板块！原本记忆量极大的40个数，就变成了5个板块。

相信读到这里，你已经记住了100~200之间的所有质数，这样的方法通俗易懂，自己推演也并不困难，所以接下来我们只列举3张图。

200~300质数分布图

300~400质数分布图

400~500质数分布图

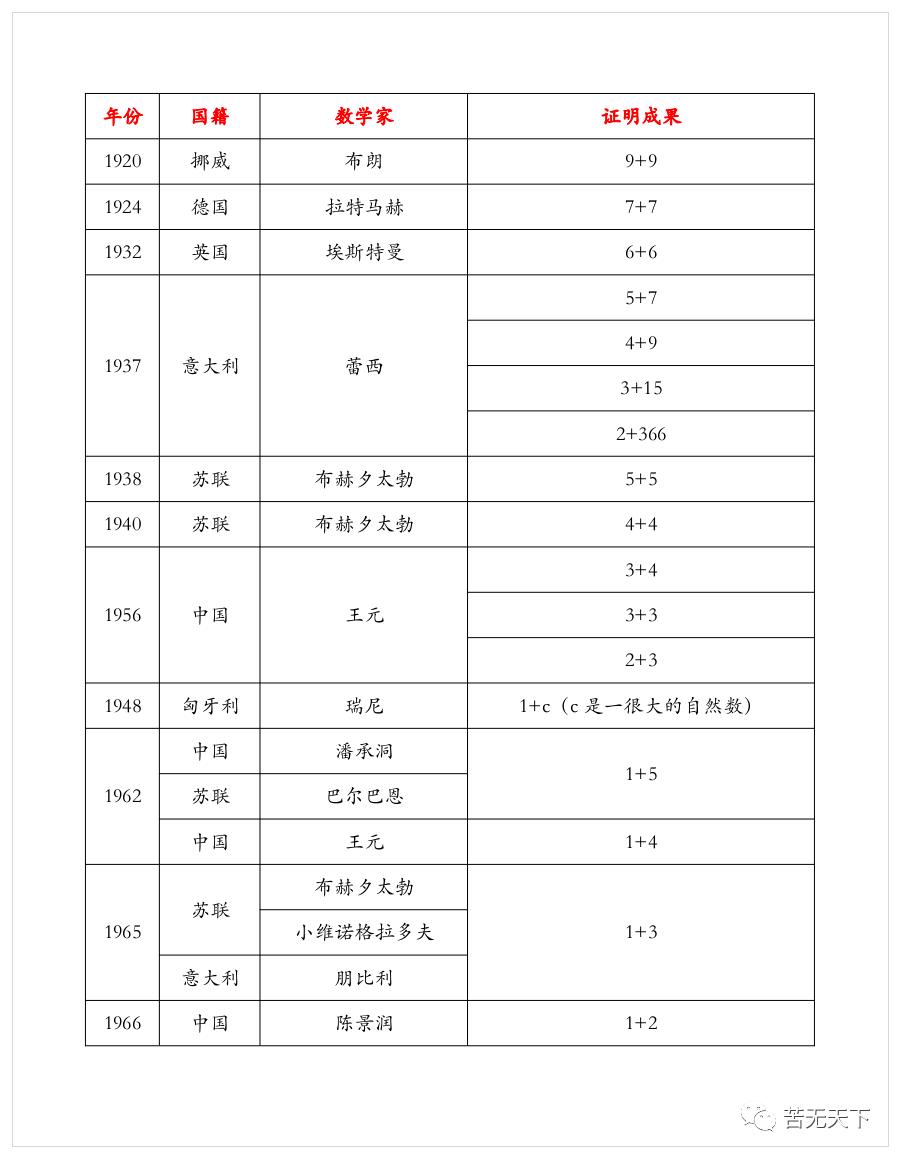
从古至今，质数一直是数学家们痴迷的话题，关于质数的讨论有很多很多，其中最著名的莫过于“哥德巴赫猜想”。

哥德巴赫1742年给欧拉的信中，哥德巴赫提出了以下猜想：任一大于2的偶数都可写成两个质数之和。但是哥德巴赫自己无法证明它，于是就写信请教赫赫有名的大数学家欧拉帮忙证明，但是一直到死，欧拉也无法证明。后来我们把命题“任一充分大的偶数都可以表示成为一个素因子个数不超过a个的数与另一个素因子不超过b个的数之和”记作“a+b”。

下面是关于“a+b”问题的历史进程：

本期的《苦无数学 | 一千以内的质数记忆法》到这里就结束了，往后每一期的苦无数学文末都会附加一道思考题，本期既然是讨论质数，那么我们就来分享一道关于质数的题目：

对于给定的质数P，求S的最小质因子。其中，

欢迎关注苦无天下，带你从上帝视角看世界！