几何学五大公理_.2 | 元 几何公理的格局（上）

Slogan

一切皆是「Ω | 元」！ 连载：9 共计6217字，预计阅读时间：0分钟 ～ 也许一辈子

本文目录

---

上部：

Ω、向渊远流长的几何学致敬！

∞、参照坐标系，可以做「Ω | ∞」种相似变换

中部：

0、过直线外任一点，可以做「Ω | 0」条平行线

1、两点，成「Ω | 1」条直线

下部：

2、直角，成「Ω | 2」种角度

3、三点，成「Ω | 3」个圆

4、线段，可以「Ω | 4」延长

Ω	向渊远流长的几何学致敬！

数学研究的对象是“数”与“形”，形的数学就是几何学．它是以直观为主导，以培养人的空间洞察力与思维为目的．从数学发展的历史来看，几何学的第一个最重要著作就是欧几里得(Euclid，约公元前330一275年)的《几何原本》．它被世界各国翻译成各种文字．它的印刷量仅次于“圣经”，所以不少人称《几何原本》为数学工作者的“圣经”。《几何原本》在数学史乃至人类思想史上有着无比崇高的地位 。 公元前3世纪。古希腊数学家欧几里德，把人们公认的一些几何知识作为定义和公理(公设)，在此基础上研究图形的性质，推导出一系列定理，组成演绎体系，写出《几何原本》，形成了欧氏几何。欧式几何分为，“平面几何”与“立体几何”。 数学概念：几何学

在数学的发展史上，东西方文化采用了不同的角度。

欧洲文明，从“ 形 ”的角度出发， 发展出来 几何学 。 而中国，从“ 数 ”的角度出发，发展出来 算术 。

为了让大家更好地了解几何学，在这里普及一下算数。

算术是数学最古老、最基础和最初等的部分，它研究数的性质及其运算。算术的内容包括两部分，一部分讨论自然数的读法、写法和它的基本运算，这一部分包括进位制和记数法，主要是 十进位制，其他的进位制与十进位制仅是采用的基数不同，都可以仿照十进位数的原理和原则进行计算，算术的另一部分包括算术运算的方法与原理的应用。如分数与百分数计算，各种量及其计算，比和比例，以及算术应用题。 数学概念：算术

几何学，最早起源于2300年前的欧几里得几何，而在二、三百年前，人类才发展出来非欧几何。

非欧几里得几何，是指不同于欧几里得几何学的几何体系，简称为非欧几何，一般是指罗巴切夫斯基几何(简称罗氏几何)和黎曼的椭圆几何。它们与欧氏几何最主要的区别在于，公理体系中采用了不同的平行公设。其中，

罗氏几何，亦称“双曲集合”。黎曼几何，亦称“椭圆几何”。

图1：欧几里得—五条公设

其中公理五又称之为平行公设(Parallel Postulate)，叙述比较复杂，并不像其他公理那么显然。这个公设衍生出“三角形内角和等于一百八十度”的定理。在高斯(F. Gauss)的时代，公设五就备受质疑，数学家罗巴切夫斯基(Nikolay Ivanovitch Lobachevski)、波尔约(Bolyai)阐明第五公设只是公理系统的一种可能选择，并非必然的几何真理，也就是“三角形内角和不一定等于一百八十度”，从而发现非欧几里得的几何学，即“非欧几何”(non-Euclidean geometry)。 几何学：平行公设

欧氏几何、罗氏几何、黎曼几何是三种各有区别的几何。这三种几何各自所有的命题都构成了一个严密的公理体系，各公理之间满足和谐性、完备性和独立性。因此这三种几何都是正确的。

在我们这个不大不小、不远不近的空间里，也就是在我们的日常生活中，欧式几何是适用的；在宇宙空间中或原子核世界，罗氏几何更符合客观实际；在地球表面研究航海、航空等实际问题中，黎曼几何更准确一些。而且黎曼几何，还是大名鼎鼎的广义相对论的数学基础。

为了更好地认识和理解数学，「Ω | 元」发展出一套「Ω | 元 ▪ 数学」体系。

「Ω | 元 ▪ 数学」，将是“数”与“形”的两位一体，犹如DNA双螺旋结构一般，同时表现出《数学》的两大基本特性：

• “数”，具有规律性，可认识和理解：数学概念
• “形”，具有空间感，可认识和理解：语文概念

正如几何学是数学早古老的起源之一，在「Ω | 元 ▪ 数学」体系中，我们将沿着先哲的道路前行，发展和完善「Ω | 元 ▪ 几何」体系。

我们以「Ω | 元 ▪ 永恒结构」来重新梳理一下欧氏几何学的五大公设：

Ω	欧氏几何学的五大公设
∞
0	过直线外任一点，可以做一条平行线
1	两点成一条直线
2	直角都相等
3	三点，成一圆
4	线段，可以无限延长

表1：欧氏几何学的五大公设

在以上「Ω | 元 ▪ 永恒结构」表中，我们很容易就发现以下问题：

欧氏几何学还不完备，只有5个公设，还缺少1个公设。

三大几何学，都不完备，都只有5个公设，都还缺少1个公设。

接下来，我们以「Ω | 元 ▪ 永恒结构」，将欧氏几何、罗氏几何和黎曼几何三大几何学，有机地融合在一起，重新梳理一下三大几何的五大公设：

Ω	三大几何学的五大公设
∞
0	过直线外任一点，可以做0、1、2、3、4、...、或∞条平行线
1	两点，成0、1、2、3、4、...、或∞条直线
2	直角，成0、1、2、3、4、...、或∞种角度
3	三点，成0、1、2、3、4、...、或∞个圆
4	线段，可以0、1、2、3、4、...、或∞延长

表2：三大几何学的五大公设 我们再制作一个新的表格，举例说明表2之中的具体涵义：

Ω	三大几何学的五大公设
∞
0	过直线外任一点，可以做0条平行线，指的是：过直线外任一点，不可以做平行线过直线外任一点，可以做1条平行线，指的是：过直线外任一点，可以做1条平行线过直线外任一点，可以做4条平行线，指的是：过直线外任一点，可以做4条平行线过直线外任一点，可以做∞条平行线，指的是：过直线外任一点，可以做无穷条平行线
1	两点可以成0条直线，指的是：两点不可以形成直线两点可以成1条直线，指的是：两点可以形成1条直线两点可以成4条直线，指的是：两点可以形成4条直线两点可以成∞条直线，指的是：两点可以形成无穷条直线
2	直角可以成0种角度，指的是：直角不可以形成角度直角可以成1种角度，指的是：直角可以有1种角度，即直角都相等直角可以成4种角度，指的是：直角可以有4种角度直角可以成1种角度，指的是：直角可以有无穷种角度
3	三点可以成0个圆，指的是：三点不可以形成圆三点可以成1个圆，指的是：三点可以形成1个圆三点可以成4个圆，指的是：三点可以形成4个圆三点可以成∞个圆，指的是：三点可以形成无穷个圆
4	线段可以0延长，指的是：线段，不可以延长。线段可以1延长，指的是：线段，可以延长到1。线段可以4延长，指的是：线段，可以延长到4线段可以∞延长，指的是：线段，可以无限延长

表3：三大几何学的五大公设其中，在表3中 标粗的内容，就是欧氏几何的五大公设。而罗氏几何和黎曼几何，以及其它新发展的几何学的五大公设，都可以在表2：三大几何学的五大公设之中找到。有兴趣的读者，可以翻阅相关几何学的文献和经典，这里不再展开详述。从表2，我们可以看到，三大几何学并不完备，还缺少第∞条公设。在此，我也第一次提出 「Ω | 元 ▪ 几何」的六大公设：

Ω	「Ω | 元 ▪ 几何」的六大公设
∞	参照坐标系，可以做0、1、2、3、4、...、或∞种自相似变换
0	过直线外任一点，可以做0、1、2、3、4、...、或∞条平行线
1	两点，成0、1、2、3、4、...、或∞条直线
2	直角，成0、1、2、3、4、...、或∞种角度
3	三点，成0、1、2、3、4、...、或∞个圆
4	线段，可以0、1、2、3、4、...、或∞延长

表4：「Ω | 元 ▪ 几何」的六大公设

将表4简化为欧式几何，就可以看到欧式几何，隐藏但没有表述的第∞条公设，参见下表：

Ω	欧氏几何的六大公设
∞	参照坐标系，可以做∞种自相似变换
0	过直线外任一点，可以做1条平行线
1	两点，成1条直线
2	直角，成1种角度，即直角都相等
3	三点，成1个圆
4	线段，可以∞延长

表5：「Ω | 欧氏几何」的六大公设

「Ω | 元 ▪ 几何」的六大公设，与「Ω | 元」的∞、0、1、2、3、4六大数字元素，有什么关系？

首先，我们作以下「Ω | 几何学」元素的定义：

Ω	几何学的六大元素定义
∞	参照坐标系
0	过直线外任一点
1	两点
2	直角
3	三点
4	线段

表6：「Ω | 几何学」的六大元素定义

其次，根据《君正之道》连载4：「Ω.0 | 元 · 原始思想的火花」(上)中第Ω节：大道至简的「Ω | 元」，中所提到的：

一切皆是「Ω | 元」。

我们可以推导出以下 「Ω｜元 ▪ 全息元法则」：若某个元素，具有0、1、2、3、4 、...、或∞种类，则表示这个元素具有一切种类，即「Ω | 一切种类元素」，即「Ω | 元素」。 元素，包含「Ω | 元素」。简单来说，就是 部分包含整体。这就是著名的全息原理：

全息理论是研究事物间所具的全息关系的特性和规律的学说。它具有部分是整体的缩影规律；反映事物之间的全息关系的全息等式。它本质上是事物之间的相互联系性，全息论既是理论科学又是应用科学，既是研究一般的全息理论，又研究一切科学领域的全息现象与全息规律。 全息理论：部分包含整体

根据这个定律和表6：「Ω | 几何学」的六大元素定义，我们就可以变换出以下表格：

Ω	「Ω | 元 ▪ 几何」的六大公设
∞	∞，包含「Ω | ∞」
0	０，包含「Ω | 0」
1	１，包含「Ω | 1」
2	２，包含「Ω | 2」
3	３，包含「Ω | 3」
4	４，包含「Ω | 4」

表7：「Ω | 元 ▪ 几何」的六大公设 佛曰，一沙一世界。

「Ω | 元 ▪ 几何」的六大公设，有什么意义？

---

我们前面提到，《数学》具有以下两大基本特性：

• “数”，具有规律性，可认识和理解：数学概念
• “形”，具有空间感，可认识和理解：语文概念

其中，「Ω | 元 ▪ 几何」所有具有的一切“形”，都可以从「Ω | 元 ▪ 几何」的六大公设之中推导出来。

另外，我们所熟知的欧氏几何、罗氏几何和黎曼几何三大几何学的五大公设，都是「Ω | 元 ▪ 几何」六大公设的投影和子集。从五大公设出发，三大几何分别都发展出来种类繁多的原理、定律和公式，这就为我们未来探索和发展「Ω | 元 ▪ 几何」的相关元原理、元定律和元公式，和建立「Ω | 元 ▪ 几何」理论体系大厦，提供了巨大的借鉴和参考作用。

在此，再次向人类的先哲们致以崇高的敬意！

∞	参照坐标系，可以做「Ω | ∞」种相似变换

我一直在想一个问题：∞，有多少种？

现在，我们知道了答案：

∞，有「Ω | ∞」种。

即可表述为，

∞＝「Ω | ∞」。

这个公式代表着，

任何一个∞，都是一个不可思议、不可描述的「Ω | ∞」。其它0、1、2、3、4元素，皆是如此。

这就是「Ω | 元 ▪ 不可思议元法则」：「Ω | 元」的任何元素，都是不可思议和不可描述的。

根据《君正之道》连载4：「Ω.0 | 元 · 原始思想的火花」(上)第Ω节，大道至简的「Ω | 元」中所确定的「Ω.0 | 元 ▪ 本源法则」第4条：

Ω	一切皆是「Ω | 元」
4	一切「Ω | 永恒元结构」都是相等的，即Ω = Ω、∞ = ∞、0 = 0、1 = 1、2 = 2、3 = 3、4 = 4

表8： 「Ω.0 | 元 ▪ 本源 法则」摘录

最准确的表达公式就是：

Ω	一切皆是「Ω | 元」
4	一切「Ω | 永恒元结构」都是相等的，即Ω＝「Ω | Ω」、∞＝「Ω | ∞」、0＝「Ω | 0」、1＝「Ω | 1」、2＝「Ω | 2」、3＝「Ω | 3」、4＝「Ω | 4」。这就是「Ω | 元 ▪ 恒等式」

表9： 「Ω.0 | 元 ▪ 本源 法则」第4条准确表达式

这个「Ω | 元 ▪ 恒等式」代表着什么？

它代表了「Ω | 元 ▪ 同种类比较元法则」：

如何知道∞？

∞＝「Ω | ∞」，即∞，等于全体的∞。

要知道∞元素，就要知道越多的∞元素。知道的∞元素越多，对∞元素的认识和理解就会越深，直到认识全体的∞元素。

如何知道0？

0＝「Ω | 0」，即0，等于全体的0。

要知道0元素，就要知道越多的0元素。知道的0元素越多，对0元素的认识和理解就会越深，直到认识全体的0元素。

如何知道1？

1＝「Ω | 1」，即1，等于全体的1。

要知道1元素，就要知道越多的1元素。知道的1元素越多，对1元素的认识和理解就会越深，直到认识全体的1元素。

2、3、4元素，皆是如此道理。

我们可以得到一下「Ω | 元 ▪ 恒等式」结构表：

Ω	「Ω | 元 ▪ 恒等式」
∞	∞＝「Ω | ∞」，即∞，等于全体的∞
0	０＝「Ω | 0」，即0，等于全体的0
1	１＝「Ω | 1」，即1，等于全体的1
2	２＝「Ω | 2」，即2，等于全体的2
3	３＝「Ω | 3」，即3，等于全体的3
4	４＝「Ω | 4」，即4，等于全体的4

表10： 「Ω | 元  ▪  恒等式」结构表

表10，告诉我们一个简单的大道理，那就是：

如果想要认识和知道”人“是什么，那么就要认识千千万万的人。认识的人越多，越能知道，反之，认识的人越少，越不知道。

如果想要认识和知道”物“是什么，那么就要认识千千万万的物。认识的物越多，越能知道，反之，认识的物越少，越不知道。

宇宙中的一切，都是如此。

「Ω | 元 ▪ 不可思议元法则」，更是告诉我们，宇宙的一切，包括灵法事物，都是不可思议和不可描述的，只能采用「Ω | 元 ▪ 同种类比较元法则」进行对比和比较，才能进行描述。

我们提到，∞可以对应的是「∞ | 罩子」。我们以「∞ | 罩子」来举例，来理解上面这句话：

「∞ | 几何学の罩子」，就是一个「Ω | 几何学の罩子」，它具有完整的「Ω | 元结构」基本模型：

图2：「Ω | 元结构」基本模型图

「∞ | 几何学の罩子」，就是一个「Ω | 几何学の罩子」

每个「∞ | 罩子」都罩着0、1、2、3、4和∞-，就是一个完整的小世界。有多少种「∞ | 几何学の罩子」，就有多少种的「∞ | 几何学」。

也就是说，

「Ω | 元 ▪ 几何」有着0、1、2、3、4、...、或∞种「∞ | 几何学」。

从「Ω | 元 ▪ 几何」的第∞公设中，我们可以得到：

Ω	「Ω | 元 ▪ 几何」的第∞公设
∞	参照坐标系，可以做0、1、2、3、4、...、或∞种自相似变换

表11：「Ω | 元 ▪ 几何」的第∞公设

怎么理解「Ω | 元 ▪ 几何」的第∞公设？我们从《君正之道》连载7：「Ω.1 | 元 · 基本原则的奠定」(中)开篇所提到的xy平面坐标系说起：

首先，我们对「Ω | xy平面坐标系」六大元素做定义，

Ω	xy平面坐标系
∞	参照坐标系
0	坐标原点，及x轴线和y轴线
1	第一象限
2	第二象限
3	第三象限
4	第四象限

表12：「Ω | xy平面坐标系」六大元素的定义

其次，在图3：xy平面坐标系这一原始的「∞ | 参考坐标系」之中，

图3：xy平面坐标系

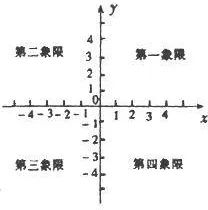
假设我们只允许存在这一原始的「∞ | 参考坐标系」，就是指不可以做「∞ | 参考坐标系」的自相似变换，这就意味着这个xy平面坐标系是固定的，不可以进行任何自相似变换，即：可以做0种自相似变换。

假设我们允许这个原始的「∞ | 参考坐标系」，只能进行一次以原点为中心的90度顺时针右旋，我们就得到了一个新的「∞ | 参考坐标系」。这也意味着可以做1种自相似变换。

从我们熟悉的世界来看，「∞ | 参考坐标系」就是「∞ | 背景」。有时候，我们需要在不同的背景下，认识和观察事物。不同的背景，就意味着不同的参照坐标系。将事物放在越多的背景下，进行认识和观察，就能越正确地认识和观察事物，反之，在越少的背景下，认识和观察事物，有可能出现误判。

∞＝「Ω | ∞」。

知道各种各样的背景，才能真正地知道：什么叫背景。

版本

作者： 君正版本号：V1.0原文创建：2020年7月9日最后更新：2020年7月9日

参考

1. 引用数学概念：几何学
2. 引用数学概念：算数
3. 引用几何学：平行公设
4. 引用全息理论：部分包含整体

引用

1. 参考公众号：君正之道
2. 参考君正之道连载1：「Ω | 元 · 历史与概述」
3. 参考君正之道连载2：「Ω.∞ | 元 · 宇宙的终极思维」(上)
4. 参考君正之道连载3：「Ω.∞ | 元 · 宇宙的终极思维」(下)
5. 参考君正之道连载4：「Ω.0 | 元 · 原始思维的火花」(上)
6. 参考君正之道连载5：「Ω.0 | 元 · 原始思维的火花」(下)
7. 参考君正之道连载6：「Ω.1 | 元 · 基本原则的奠定」(上)
8. 参考君正之道连载7：「Ω.1 | 元 · 基本原则的奠定」(中)
9. 参考君正之道连载8：「Ω.1 | 元 · 基本原则的奠定」(下)

---

「Ω | 君正之道」          

---

Copyright © 2019-2020 君正之道 无漏之学 版权所有