原理图框图_第四讲 控制系统的方框图

金鸡一唱天下白：第三讲 控制系统的复域数学模型(传递函数)​zhuanlan.zhihu.com

自动化人 - 知乎​www.zhihu.com

在控制工程中，为了便于对系统进行分析和设计，常将各元件在系统中的功能及各部分之间的联系用图形来表示，即方框图和信号流图。

由具有一定函数关系的环节组成的，并标明信号流向的系统的方框图，称为系统的结构图。系统的结构图实质上是系统原理图与传递函数两者的综合。可以清楚地表示出系统的结构和各部分信号的流向。

4.1方框图

控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。

方框图也称方块图或结构图，具有形象和直观的特点。系统方框图是系统中各元件功能和信号流向的图解，它清楚地表明了系统中各个环节间的相互关系。构成方框图的基本符号有四种，即信号线、比较点、传递环节的方框和引出点。

方框图元素

（1）方框（Block Diagram）:表示输入到输出单向传输间的函数关系。方框图也称方块图或结构图，具有形象和直观的特点。系统方框图是系统中各元件功能和信号流向的图解，它清楚地表明了系统中各个环节间的相互关系。构成方框图的基本符号有四种，即信号线、比较点、传递环节的方框和引出点。

信号线：带有箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或象函数。

（2）比较点（合成点、综合点）Summing Point

两个或两个以上的输入信号进行加减比较的元件。“+”表示相加，“-”表示相减。“+”号可省略不写。

注意：进行相加减的量，必须具有相同的量刚。

(3)分支点（引出点、测量点）Branch Point

表示信号测量或引出的位置注意：同一位置引出的信号大小和性质完全一样。

4.2系统方框图的绘制

对于一个系统在清楚系统工作原理及信号传递情况下，可按方框图的基本连接形式，把各个环节的方框图连接在一起，构成系统方框图。

（1）考虑负载效应分别列写系统各元部件的微分方程或传递函数，并将它们用方框（块）表示。

（2）根据各元部件的信号流向，用信号线依次将各方块连接起来，便可得到系统的方块图。

系统方块图-也是系统数学模型的一种。

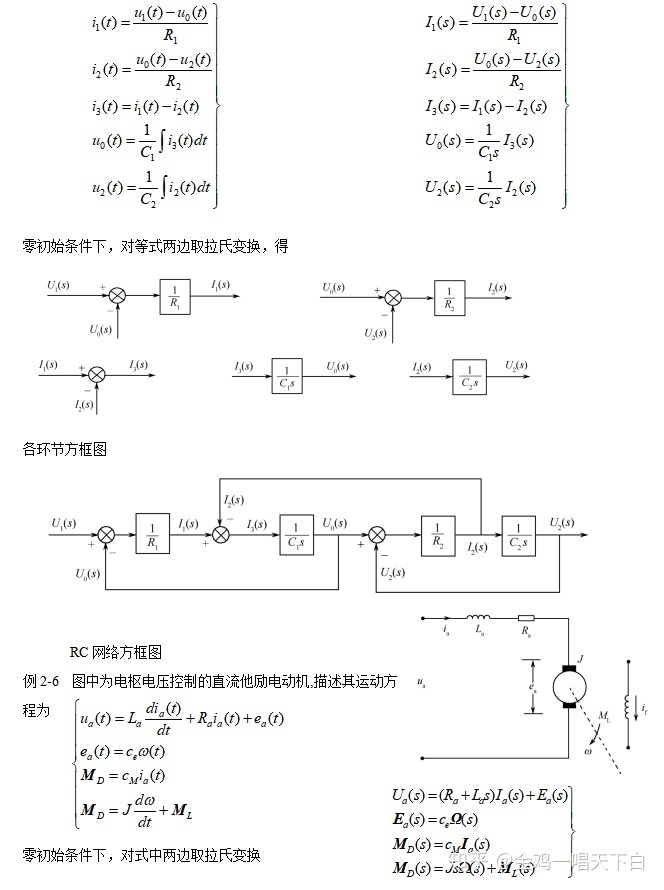
例2-5 图中为一无源RC网络。选取变量如图所示，根据电路定律，写出其微分方程组为

几个基本概念及术语

(1)前向通路传递函数

假设N(s)=0 ， 打开反馈后，输出C(s)与R(s)之比。等价于C(s)与误差E(s)之比

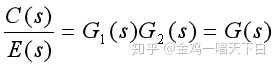
(2)反馈回路传递函数 假设N(s)=0 主反馈信号B(s)与输出信号C(s)之比。

(3)开环传递函数 Open-loop Transfer Function

假设N(s)=0 主反馈信号B(s)与误差信号E(s)之比。

(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0

输出信号C(s)与输入信号R(s)之比。

推导：因为

右边移过来整理得

请记住

(5)误差传递函数

假设N(s)=0 误差信号E(s)与输入信号R(s)之比 。

将

代入上式，消去G(s)即得：

(6)输出对扰动的传递函数 假设R(s)=0

输出对扰动的结构图

利用下列公式，

直接可得：

（7）误差对扰动的传递函数 假设R(s)=0

误差对扰动的结构图

线性系统满足叠加原理，当控制输入R(s)与扰动N(s)同时作用于系统时，系统的输出及误差可表示为：

注意：由于N(s)极性的随机性，因而在求E(s)时，不能认为利用N(s)产生的误差可抵消R(s)产生的误差。

4.3环节间的连接

环节的连接有串联、并联和反馈三种基本形式。

1.串联 :在单向的信号传递中，若前一个环节的输出就是后一个环节的输入，并依次串接如图2-32所示，这种联接方式称为串联。

n个环节串联后总的传递函数 :

即环节串联后总的传递函数等于串联的各个环节传递函数的乘积。

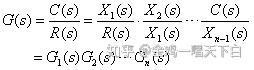
2.并联 :若各个环节接受同一输入信号而输出信号又汇合在一点时，称为并联。

3.反馈：若将系统或环节的输出信号反馈到输入端，与输入信号相比较，就构成了反馈连接，如图所示。如果反馈信号与给定信号极性相反，则称负反馈连接。反之，则为正反馈连接，若反馈环节H(s)=1称为单位反馈。

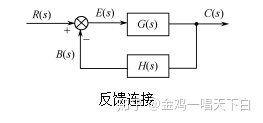
反馈连接后，信号的传递形成了闭合回路。通常把由信号输入点到信号输出点的通道称为前向通道；把输出信号反馈到输入点的通道称为反馈通道。

对于负反馈连接，给定信号r(t)和反馈信号b(t)之差，称为偏差信号e(t) 即

通常将反馈信号B(s)与误差信号E(s)之比，定义为开环传递函数，即

4.4方框图的变换和简化

有了系统的方框图以后，为了对系统进行进一步的分析研究，需要对方框图作一定的变换，以便求出系统的闭环传递函数。

方框图的变换应按等效原则进行。所谓等效，即对方框图的任一部分进行变换时，变换前、后输入输出总的数学关系式应保持不变。除了前面介绍的串联、并联和反馈连接可以简化为一个等效环节外，还有信号引出点及比较点前后移动的规则。

方块图的绘制

例2-7化简图(a)所示系统方框图，并求系统传递函数

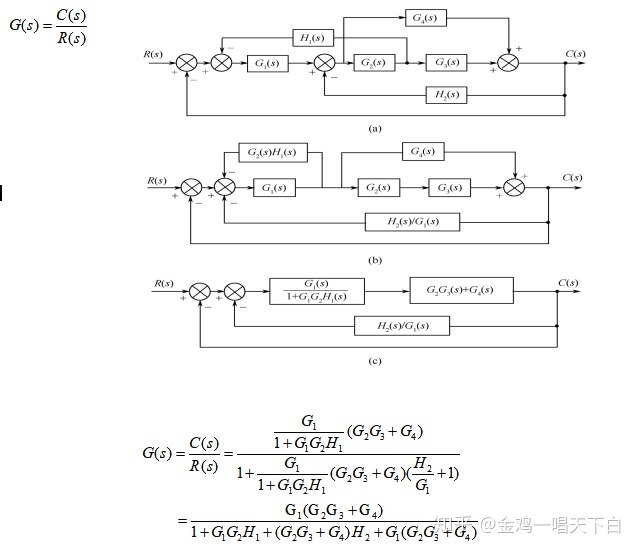
例2-8 试化简如图2-37 (a)所示系统的方框图，并求闭环传递函数。

图2-37 (a)是一个交错反馈多路系统，采用引出点后移或前移，比较点前移等，逐步变换简化，可求得系统的闭环传递函数为

图2-37 方框图的变换与简化

6个基本术语

前向通路传递函数、

反馈传递函数、

开环传递函数、

闭环传递函数、

误差（对输入）传递函数、

输出对扰动传递函数

金鸡一唱天下白：第五讲 信号流图​zhuanlan.zhihu.com

自动化人 - 知乎​www.zhihu.com

注：版权属笔者所有，如需转载请务必联系！

最后说一句：码字不易，若此文对你有启发，收藏前请点个赞、点点喜欢，是对知乎主莫大的支持！！

参考

1.^如有侵犯您的权益，请联系作者删除。