同指数幂相减公式_别忽视对数运算中的小公式，关键时刻有大用处，高中数学_高考数学复习...

别忽视对数运算中的小公式，关键时刻有大用处，高中数学_高考数学复习。

幂的指数部分是一个同底的对数时，结果等于对数的真数。使用这个公式时要注意，幂的指数部分必须是一个纯对数，即必须是一个单独形式的对数，对数的前面不能出现系数，也不能出现别的项。

01、幂的底数是根号3，对数的底数是3，只需把根号3化成分数指数幂的形式，即可使两个底数相同，即都为3，详细过程如下。

02、幂的指数部分是两项的和，不是一个单独的对数，故不能使用上面的对数公式，只需要使用同底数幂乘法的逆用公式稍加变形即可，详细如下：

03、只要你能观察出幂的底数与对数的底数互为相反数这一特点，你就成功了一半，剩下的任务就是变形，使之符合上面的公式即可。03、只要你能观察出幂的底数与对数的底数互为相反数这一特点，你就成功了一半，剩下的任务就是变形，使之符合上面的公式即可。

对数公式(1)的用法是：真数的指数可以移到对数前面作为对数的系数，反过来，对数的系数也可以移到真数的头上作为真数的指数，在对数运算中，这两种用法都常常会用到。对数公式(2)实际上是是由(1)得到的，它最常的用法是：真数进行n次方，同时对数乘以1/n，对数的值保持不变，这个结论很容易理解，在此不做过多讨论。

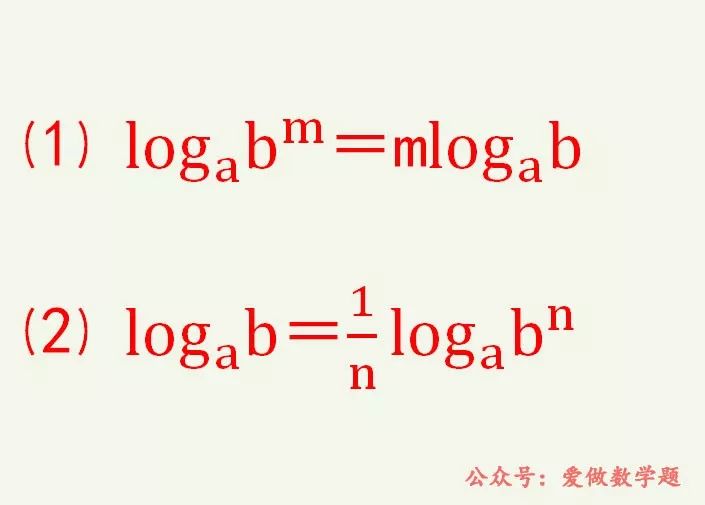
第1题，等式左边可以使用公式(1)变成单个的对数，右边使用同底对数加法公式也可以变成单个的对数，之后根据同底对数相等，则真数相等，得到M和N之间的关系式，最终就可以求出M/N的值。要注意的是：不要忘了对数的真数大于0这一隐含条件。

第2题，真数是两个复杂的二次根式的差，二次根式又无法开方，对于这种二次根式常常通过加平方的方法去根号，所以考虑使用上面的公式(2)进行计算，详细过程如下。

温馨提醒：公众号菜单处可以查看分类的课程和专题。