利用matlab统计一张图中线段的数量_北师大七上数学4.2比较线段的长短知识点精讲...

知识点总结

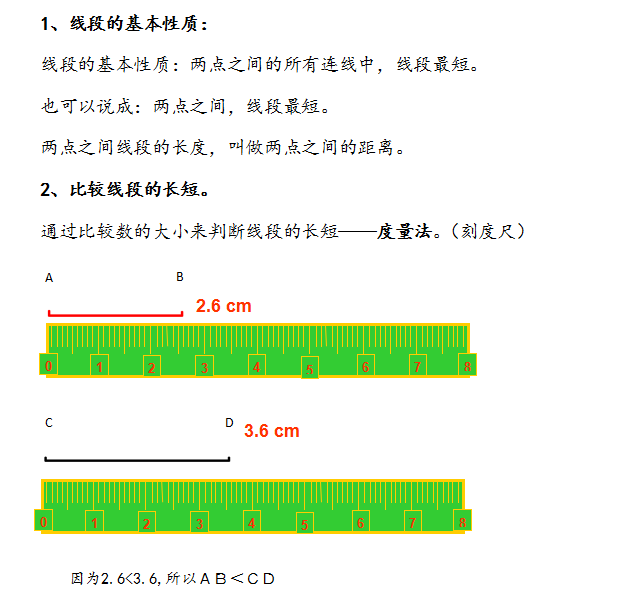
1、线段的性质：两点之间，线段最短。

2、两点之间的距离：两点之间线段的长度叫做两点之间的距离。

3、比较线段长短的方法：(1)目测法；(2)度量法；(3)叠合法

4、线段的中点：在线段上，到线段两个端点距离相等的点叫做线段的中点。

5、尺规作图：用没有刻度的直尺和圆规作图

6、用尺规作线段：

(1)作一条线段等于已知线段；

(2)作一条线段等于已知线段的二倍；

(3)作一条线段等于已知线段的和或差。其方法是相同的，都是先画一条射线，然后用圆规在射线上截取即可，注意保留作图痕迹，画完图形后写出总结“某某线段即为所求作的线段”。

尺规作图的定义：仅用圆规和没有刻度的直尺作图的方法叫做尺规作图． 

要点诠释：

(1)只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题．

(2)直尺必须没有刻度，无限长，且只能使用直尺的固定一侧.只可以用它来将两个点连在一起，不可以在上面画刻度．

(3)圆规可以开至无限宽，但上面也不能有刻度.它只可以拉开成之前构造过的长度．

2.线段的中点：如下图，若点B在线段AC上，且把线段AC分成相等的两条线段AB与BC，这时点B叫做线段AC的中点．

3. 用尺规作线段或比较线段

(1) 作一条线段等于已知线段：用圆规作一条线段等于已知线段．例如：下图所示，用圆规在射线AC上截取AB＝a．

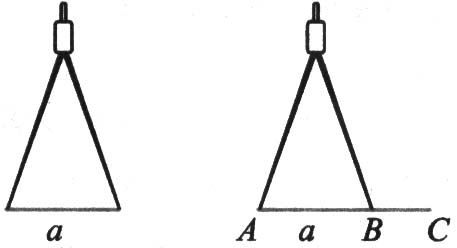
要点诠释：几何中连结两点，即画出以这两点为端点的线段.

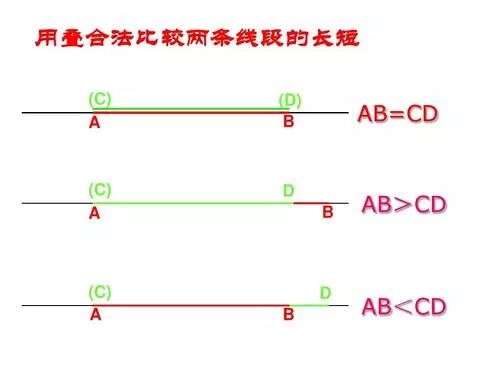
(2)线段的比较：

叠合比较法：利用直尺和圆规把线段放在同一条直线上，使其中一个端点重合，另一个端点位于重合端点同侧，根据另一端点与重合端点的远近来比较长短．如下图：

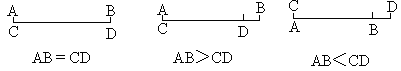
要点诠释：线段的比较方法除了叠合比较法外，还可以用度量比较法．

 如图所示，在一条笔直公路a的两侧，分别有A、B两个村庄，现要在公路a上建一个汽车站C，使汽车站到A、B两村的距离之和最小，问汽车站C的位置应如何确定?

【答案与解析】

解：如图，连接AB与直线a交于点C，这个点C的位置就是符合条件的汽车站的位置．

【总结升华】“两点之间线段最短”在实际生活中有广泛的应用，此类问题要与线段的性质联系起来，这里线段最短是指线段的长度最短，连接两点的线段的长度叫做两点间的距离，线段是图形，线段长度是数值．

举一反三：

【变式】 (1)如图1所示，把原来弯曲的河道改直，A、B两地间的河道长度有什么变化?

(2)如图2，公园里设计了曲折迂回的桥，这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比，这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理．

【答案】

解：(1)河道的长度变小了．

     (2)由于“两点之间，线段最短”，这样做增加了游人在桥上行走的路程，有利于游人更好地观赏湖面风光，起到“休闲”的作用．

思维导图 

教学设计

一、教材分析：

1、教材的地位和作用

本节课是教材第五章《平面图形及其位置关系》的第二节，是平面图形的重要的基础知识。通过上一节课的学习，学生了解了线段的定义和表示方法，这一节将从学生的生活经验出发，抽象提炼线段的基本性质，线段的大小比较方法等。这对学生几何意识的起步、基本的操作方法、几何语言的培养、乃至后期几何图形的学习都具有重要的作用。

2、学情分析

鉴于学生的认知水平和几何方法才起步，教学中要始终遵守学生主动学习的原则，低起点、多铺垫，多给学生思考的时间，让学生动手操作。同时利用多媒体辅助教学拓展学生的思维，初步培养学生的几何语言的规范性。

3、教学重、难点

教学重点：了解线段性质及线段的比较方法，能用圆规作一条线段等于已知线段，掌握两点之间的距离的概念和线段中点的概念.

教学难点：

1.掌握线段比较的正确方法.

2.线段中点的表示方法及应用.

二、教学目标

(一)知识与技能：借助于具体情景中了解“两点之间线段最短”的性质；能借助于尺、规等工具比较两条线段的大小；能用圆规作一条线段等于已知线段，掌握线段的中点的表示方法及应用。

(二)过程与方法：通过思考想象、合作交流、动手操作等数学探究过程，了解线段大小比较的方法策略，学习开始使用几何工具操作方法，发展几何图形意识和探究意识。

(三)情感态度与价值观：在解决问题的过程中体验动手操作、合作交流、探究解决的学习过程，激发学生解决问题的积极性和主动性。

三、教学方法

　结合本节课内容和学生实际我采用了如下教学法：即引导发现式的教学方法并充分利用多媒体辅助教学；在教学时，调动学生动手、动脑、共同探索来寻求解决问题的方法。

四、教学资源：

   班班通多媒体课件

五、教学流程：

(一)、创设情境，引入新课  

(二)、小组合作，探索新知

(三)、小试牛刀，应用实践

(四)、知识归纳，情感升华

(五)、当堂检测，及时反馈

(六)、布置作业，课后巩固

六、教学设计思路

本课首先从学生已有的生活经验出发，设计活动，通过学生讨论，得出身高比较及模拟试验；培养学生思考问题的开放性，然后通过类比的思想得出线段比较的三种方法，并通过折纸的过程中，发现线段中点。整堂课的教学活动中，本着体现学生的主动性、参与性，在自主探索，合作交流的过程中，真正理解和掌握基本数学知识，实际几何语言的书写，培养学生的实际能力、合作能力及创新能力。

七、教学过程：

教学环节	教师活动	学生活动	设计意图
一 创 设 情 境 ， 引 入 新 课	1、生活中的数学： 多媒体出示生活中“猫狗获取食物”的图片，让学生猜测它们的走法。 提出问题：小狗、小猫为什么都选择直的路？ 2、用多媒体出示一张图片，让学生猜测“从A到C的四条道路，哪条最短？” 发现结论：两点之间的所有连线中，线段最短. 简述为：两点之间线段最短。 顺利的引出定义：两点之间线段的长度，叫做这两点之间的距离 3、能否说 “线段就是距离”？ 不能说线段是距离。 线段是图形，距离是长度，它是一个数量，且有长度单位。 4、联系生活，课外拓展： 如图：这是A、B两地之间的公路，在公路工程改造计划时，为使A、B两地行程最短，应如何设计线路？在图中画出。你的理由是                      .	积极参与观察、讨论、交流、总结. 学生发言,易于得出线段AC最短 学生分小组讨论，找代表起来发表看法。 找一个同学起来回答，现学现用。	通过学生积极参与和播放多媒体图片，创设情境，引入线段长短的比较，既激发学生学习新知识的兴趣，又让不同的学生获得不同的体验.  通过田径赛跑中跑道的长度来说明线段不是距离更具有说服力。 从学生熟悉的生活实例导入，使学生体会到“两点之间，线段最短”的性质 。
二 小 组 合 作 ， 探 索 新 知	1、在班上找两个同学比身高。怎样比较的？   ①找两个身高差的很大的同学(观察) ②找两个身高差不多的同学(比较) 教师有意叫矮一点的同学站在讲台上，高一点的同学站在讲台下背靠背比高. 学生会反对，指出应脚根靠脚根，背靠背。 趁机提出为什么要站在一起，脚根靠脚根，背靠背？ 2、给你两根筷子，你能比较出它们的长短吗? 　　学生容易想到下列两种方法： ①先用尺子量出它们的长度，然后根据长度比较出它们的长短。 ②把一根筷子捏在一起，使它们的一端对齐，就可比较出它们的长短。 教师强调比较时要注意：一头对齐，几根紧靠，观察另一头的位置。这就为后续两线段大小比较作铺垫。 由生活中比较长短引出两条线段如何比较长短呢？(将实际问题转化为数学问题) 3、用什么方法比较两条线段的长短？ 方法一：观察法： 图中观察法不能得出：AB=CD，可见观察法不可靠。 方法二：度量法(从“数值”的角度)： 用刻度尺量出两条线段的长度，再进行比较(实质上是比较数的大小。测量中不管如何的细致，总会有误差。) 方法三：叠合法(从“形”的角度)： ①生活中如何比较两根绳子的长短、两个同学的身高？ 提出问题：类比上面的方法怎样比较线段的长短？ ②叠合法：将两条线段的各一个端点对齐，看另一个端点的位置． 结果有三种情况：大于、小于、等于. 如图(1)，线段AB与线段DC相等，记作：AB=CD. 如图(2)，线段AB大于线段CD，可记作：AB>CD. 如图(3)，线段AB小于线段CD，可记作AB<CD. 4、动手操作，尺规画出一条线段等于已知线段吗？ 针对刚才的比较筷子继续提出问题：筷子能很方便地移动，你能把任一条线段移动到你纸面上吗？如果不用刻度尺还能用什么更为简便的工具来移动它？-----圆规 用叠合法比较线段的长短，首先要学会如何用圆规作一条线段等于已知线段。 例题：已知线段a，用尺规作一条线段AC等于已知线段a 第一步：先用直尺画一条射线AB. 第二步：以A为圆心，在射线AB上截取线段AC=a. 所以，线段AC就是所求的线段. (注意：要求学生不必写画法，但最后必须写好结论) 5、线段的中点 (1)在半透明纸上画一条线段AB，折纸使A和B重合，将纸展开后，在线段AB上折痕处描点M。 教师提出问题：线段AM和BM 的大小关系是什么？线段AM和AB的大小关系是什么？   (学生先折、师生交流) (2)怎样将一根绳子分成相等的两段？ (3)线段的中点(从学生的回答中，归纳出线段中点的定义) 用几何语言表示：  ∵点M是线段AB的中点 6、例题解析 在直线上顺次取A、B、C三点，使得AB=4㎝,BC=3㎝.如果O是线段AC的中点，求线段OB的长度。 解：因为线段AC=AB+BC=7 cm，O是线段AC的中点， 所以OA=AC=3.5 cm, 而线段OB=AB－OA=0.5 cm. 因此，线段OB的长度是0.5 cm. 解：∵AB=4cm  BC=3cm ∴AC=AB+BC=7cm ∵O是线段AC的中点 ∴OA=AC=3.5cm ∵OB=AB－OA ∴OB =4－3.5=0.5cm	学生容易想到下列两种方法1、两人自报身高 2、把他 们拉在一起比一比。 将课前准备好的两根长短不一的筷子拿出来，请一名学生上讲台操作。 学生自由发言 学生动手操作 将学生前后位分组，进行学中做，先独立思考，有疑问的鼓励学生合作探讨，生生互动，进行“学中做”	与生活中的比较长短、身高类比，引入线段长短的比较，使学生更容易理解比较线段长短的方法。 教学中注意问题呈现的层次性，可直接观察判断到难以直接观察判断，这样不仅有利于学生体会比较线段大小的必要性，而且有利于从中归纳比较线段长短的方法，体现数学来源于生活，与服务于生活的理念，调动学生学习热情，掌握比较方法。 通过折纸、把绳子分成相等的两段等生活实例，更能加深学生对线段中点定义的理解，基础练习有助于巩固方法，阶梯训练则突出了不同学生得到不同发展这一理念，同时可以巩固对线段中点表示方法的掌握，训练学生规范的几何语言。 两种格式的书写方式以给学生参考
三 小 试 牛 刀 ， 应 用 实 践	1、如图，从A到B有4条道路，为了节约时间，你会选择    条路。原因是                         。 2、下面的线段中，哪条线段最长？哪条线段最短？ (鼓励学生用两种方法进行比较) 答案：自左向右，第三条线段最长，第一条线段最短. 3、概念理解： (1)判断：若AM=BM,则M为线段AB的中点。(    ) 反例：等腰三角形。线段中点的条件： ①、在已知        上。  ②、把已知线段分成两条       线段的点. (2)如图，AB=8㎝,CB=5㎝，D是AC的中点，求DC的长。 解：∵ AB=8㎝,CB=5㎝ ∴ AC=______—_______ =______—_______    =______ ∵ D是AC的中点 ∴ DC=_______=_______=_______	先小组讨论在到全班讨论交流，二至三人上讲台口述解题思路，供其他同学评议，开阔思路．	根据不同层次的学生设计不同层次的问题，引导学生“做中学” ，体验数学，感受数学，体现学以致用。
知识 归纳 ， 情感 升华	1、线段的性质：两点之间的所有连线中，线段最短. 2、两点间的距离的概念 3、线段比长短的两种方法：重合法和度量法. 它们分别从“形”和“数”的角度来比较线段的长短. 4、线段的画法：用圆规和直尺画一条线段等于已知线段. 5、线段中点的定义及表示方法。.	学生先自述学会了什么，找几位学生谈收获和体会。	培养学生自我总结自我评价能力，学会把零散的知识点进行整和优化，完善自己的知识构件。
当堂 检测 ， 及时 反馈	一、基础巩固 1.连结_______的_______叫作两点间的距离. 2.点B把线段AC分成两条相等的线段，点B就叫做线段AC的_______，这时，有AB=_______,AC=_______BC，AB=BC=_______AC. 3.思考：若MA=MB，则M是线段AB的中点.(     )(填“√”“×”) 二、填空题 1.如图，点C分AB为2∶3,点D分AB为1∶4，若AB为5 cm,则AC=_______cm,BD=_______cm,CD=_______cm. 2.下面线段中，_______最长，_______最短. 按从长到短的顺序用“>”号排列如下： 3.若线段AB=a,C是线段AB上任一点，MN分别是AC、BC的中点，则MN=_______+_______=_______AC+_______BC=_______. 三、比较下列各组线段的长短 (1)线段OA与OB.  (2)线段AB与AD.             (3)线段AB、BC与AC.  四、解答题 1.已知两条线段的差是10 cm，这两条线段的比是2∶3,求这两条线段的长. 2.在直线AB上，有AB=5 cm，BC=3 cm，求AC的长.  解：(1)当C在线段AB上时，AC=_______. (2)当C在线段AB的延长线上时，AC=_______.	根据所学内容有针对性的设计当堂检测题，给学生限时独立完成。 讲评时学生同桌之间交换批阅。	通过当堂过关训练来达到一个反馈的目的。
布置 作业 课后 巩固	1、基础作业：课本P8    习题5.2  1、2、3、4 2、拓展作业： 在直线上取A、B、C三点，使得AB=4㎝,BC=3㎝.如果O是线段AC的中点，求线段OB的长度。	学生课下完成。	作业分层布置，可以使学生根据自己的实际情况选择适合自己的作业，避免“一刀切”的局面，有助于提高学生学习数学的积极性。

八、板书设计

§5．2比较线段的长短

一、线段的性质                               

二、两点之间的距离                           

三、线段长短的比较

四、尺规作图

①：观察法

②：度量法(从“数值”的角度)

③：叠合法(从“形”的角度)

五、线段的中点

六、课堂练习

七、课时小结

八、课后作业

九、教学后记

由于学生刚接触几何知识，本节内容虽说难度不大，但知识点多，容量较大，学生学起来会觉得有些累。但本节课设置的问题情境贴近学生生活,可以很好的解决从形象到抽象的过程。在教学过程中，通过多媒体演示一些简单的动画效果，既增加趣味性，又直观，有利于提高学生的学习兴趣.同时，穿插学生猜想，动手操作，合作交流的内容，既能启发学生积极思考，又能使学生体会与他人合作的重要性。本节内容也渗透了分类的数学思想。一些拓展题能让学得更好的学生吃饱，也起到举一反三，一题多变的作用。

声明：素材来源于网络，本公众号免费为学生提供优质的学习资源，无任何商业用途，如有不妥，请与小编联系处理(微信号：chqyy58)。