lisp xy轴不等比缩放_双指缩放的计算

问题描述 在支持触屏的设备中，我们经常会用到双指缩放的功能。 这里我们不讨论双指缩放的触发逻辑，我们假设双指缩放已经发生了，而且我们知道上一次两个触摸点的坐标(p0, p1)，以及当前两个触摸点的坐标(p0’，p1’)，我们讨论一下缩放的相关参数应该怎么计算。 常见解法 最常见的方法是，计算上一次两个点(p0, p1)之间的距离d0，以及当前两点(p0’，p1’)之间的距离d1，然后计算缩放值s = d1/d0。我们知道，当我们对一个可视对象进行缩放时，默认是以对象的本地坐标系的坐标原点进行缩放的，所以，我们还要计算缩放的中心点，否则缩放结果并不是我们预期的效果。缩放中心点也很好算，我们可以取当前两个点的中心点作为缩放的中心点，p = (p0’ + p1’) / 2。 常见解法中的问题 场景1

当我们固定一个一个手指，只移动另一个手指的时候，我们想要的结果是:固定的手指处应该是不动的。上面的方法是以两个手指的中心点为缩放中心，显然是达不到预期的效果的。

场景2

当我们将两个手指同时移动，并保持两个手指之间的间距不变时，场景跟随手指移动才比较合理。按照上面的方法，场景不会有任何变化，显然不是我们想要的效果。

对于第一种，可能会提出这样一种方法，判断如果一个手指不动，就以不动的手指为中心进行缩放。 对于第二种，可能会提出这样一种方法，先提取两个手指的公共偏移量，用作平移，减去公共偏移量之后，再计算缩放。 这样针对特殊场景，做特殊处理的方式，当然可以解决问题，但是只能解决个别问题，无法从根本上解决问题，换个场景就不实用了，还要再加其它特殊处理。能不能有一种通用的方案，从根本上解决这个问题。 问题分析、求解 我们把问题抽离出来。我们现在知道两个点(p0，p1)，经过以某个点(p)为中心的缩放(缩放值为s)之后，再经过平移(平移向量为m)，变成了点(p0’，p1’)。求p、s、m。 考虑旋转平移缩放，求精确解 我们知道，一个点到另一个点的变换，相当于一个变换矩阵左乘这个点。也就是有： p0’ = A · p0 p1’ = A · p1 我们以二维为例，变换矩阵

无法看到公式请关闭手机深色模式 只考虑旋转平移缩放，而且让xy轴等比缩放，不考虑斜切的话，变换矩阵可以变为

无法看到公式请关闭手机深色模式

其中 a = s * cos(q)，b = s * sin(q)，其中s是缩放值，q是旋转角度。tx、ty是平移量。 变换矩阵中有4个未知量。p0->p0’的变换可以列出两个方程，p1->p1’的方程也可以列出两个方程，4个方程，4个未知量，可解。 很好理解，我们把两个手指想象成两个钉子，场景想象成一块橡皮膜，两个钉子扎到橡皮膜上，当移动两个钉子时，橡皮膜会旋转平移缩放，来保证钉子下的两个点是不动的，状态是确定的，一定存在一种变换来满足状态之间的切换。 忽略转转求近似解 然而这并不是我们想要的结果，我们只想要平移和缩放，不想要旋转。 去掉旋转的变换矩阵是这样的

无法看到公式请关闭手机深色模式

3个未知数，4个方程，显然无解。但是我们可以求近似解。 以为这样就结束了？ 并没有这么简单。直接丢弃旋转是不行的。因为我们上边的变换是以坐标原点为中心的，直接丢弃旋转造成的误差太大了。如果丢弃以实际旋转的中心点为原点的旋转，还是可以接受的。 求缩放值 有 s * s = a * a + b * b，很容易求出s。 求旋转中心点 我们已经求出了精确的变换。我们可以求出这个变换下的不动点，这个不动点作为实际缩放的中心点，应该是可行的。 也就是解 A · p = p。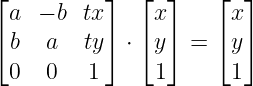

无法看到公式请关闭手机深色模式

看起来好难解。 其实并不难，我们把方程列出来： a * x - b * y + tx = x; b * x + a * y + ty = y; 化简一下： (a - 1) * x -b * y + tx = 0; b * x + (a - 1) * y + ty = 0; 很容易解出： x = -((a - 1) * tx + b * ty) / ((a - 1) * (a - 1) + b * b) y = -ty / (a - 1) 或 ((a - 1) * x + tx) / b (两个结果应该是一样的，分母不能为0) 求平移向量 缩放值和缩放中心点已经算出来了，再算出平移量就大功告成了。 A · p = p’

无法看到公式请关闭手机深色模式

展开

无法看到公式请关闭手机深色模式

其中p0(x0,y0)、p0’(x0’,y0’)、p1(x1,y1)、p1’(x1’,y1’)、s均为已知，求tx、ty。 转化成未知数为tx、ty的方程： tx = x0’ - x - s * (x0 - x); ty = y0’ - y - s * (y0 - y); tx = x1’ - x - s * (x1 - x); ty = y1’ - y - s * (y1 - y); 矩阵形式：

无法看到公式请关闭手机深色模式

4个方程，两个未知数，4个方程必然是线性相关的。方程无解，但是我们可以求其最小二乘解。 最小二乘法求解 AX = Y，结果为 X = (AᵀA)⁻¹AᵀY。效果

总结 看起来很简单的功能，做好做细也很复杂。 任何一个小问题，深入去研究，都很有意思。 关于双指缩放的问题，网上一搜，都是千篇一律的，也都是使用最简单的方式，没有深入分析。 希望上面的分析能起到抛砖引玉的作用。肯定有更简单的解法能得到相同的结果(或者更合理的结果)，作者水平有限，只能到这里了。如果大神有更好的解法，望不吝赐教。