总结
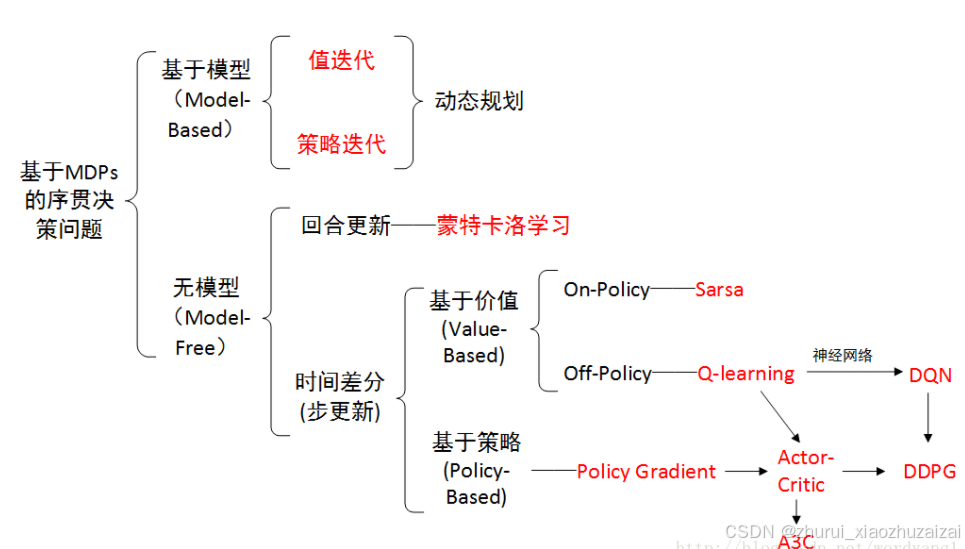
想象你在玩一款“走迷宫拿金币”的游戏:
- REINFORCE:你随便乱走,拿到金币后记住“刚才哪几步管用”,下次多走这些路;掉坑里就记住“刚才哪几步坑爹”,下次少走。但它要等一局结束才知道好坏,效率低但简单。
- Actor-Critic:你(Actor)负责走路,旁边有个教练(Critic)实时点评“这步走得好/差”,你立刻调整。不用等结束,效率更高。
- A2C(Advantage Actor-Critic):教练变聪明了,不仅说“这步好不好”,还会说“这步比平均水平好多少”,让你调整更精准。
- A3C(Asynchronous A3C):你找来一群“分身”同时玩游戏,有的走左路,有的走右路,大家随时分享经验,学起来飞快!
从学习的函数分类
基于价值函数的强化学习算法
学习价值函数,然后根据价值函数导出一个策略,学习过程中并不存在一个显示的策略
有动态规划算法(DP)、蒙特卡洛方法(MC)、时序差分算法(TD)(SARSA和Q-learning)、DQN及DQN的改进算法等。基于策略函数的强化学习算法
直接显式地学习一个目标策略
有策略梯度算法(REINFORCE)。基于价值函数和策略函数的强化学习算法。
价值函数和策略函数均学习,学习到最优策略和最优价值函数,
有AC(Actor-Critic)算法、信任区域策略优化算法(TRPO)、PPO算法、深度确定性策略梯度算法(DDPG)以及SAC(Soft Actor-Critic)算法等
根据是否有环境模型【环境模型(model)是指状态转移函数和奖励函数】
基于模型的强化学习(Model-based RL)
基于模型的强化学习中的模型可以是事先知道的,也可以是根据智能体与环境交互采样到的数据学习得到的,然后用这个模型帮助策略提升学习到最优策略或者价值估计学习到最优价值函数,
有动态规划算法(DP)(模型是事先知道的)、Dyna-Q算法(环境是采样学到的)无模型的强化学习(Model-free RL)
根据智能体与环境交互采样到的数据直接进行策略提升学习到最优策略或者价值估计学习到最优价值函数,
有蒙特卡洛方法(MC)、时序差分算法(TD)(SARSA和Q-learning)、DQN及DQN的改进算法、策略梯度算法、(REINFORCE)、AC(Actor-Critic)算法等大量算法。
白盒环境与黑盒环境
白盒环境:知道环境的状态转移函数P(s’|s)或P(s’|s,a)和奖励函数R(s)或R(s,a):
白盒环境下的学习相当于直接给出了有监督学习的数据分布(就是有了目标靶子),不需要采样了,直接最小化泛化误差更新模型参数。
对于马尔可夫决策过程(MDP),在白盒环境下(即known MDP),就可以直接用动态规划算法(策略迭代算法、价值迭代算法)求解出最优状态价值函数和最优策略(控制),或者求出某一策略下的价值函数(预测)。黑盒环境:不知道环境的状态转移函数P(s’|s)或P(s’|s,a)和奖励函数R(s)或R(s,a):
黑盒环境就只能采集数据,尽可能的靠近靶子学习,即最小化数据的误差更新参数(训练出的模型是否接近真是模型就要看采集的数据的量)。
大部分强化学习现实场景,马尔可夫决策过程(MDP)是黑盒环境。对于马尔可夫决策过程(MDP),在不知道环境的状态转移函数和奖励函数下(或者是known MDP,但环境太大太复杂无法去使用)就使用无模型的强化学习算法和基于模型的强化学习算法算出最优策略和最优价值函数(控制),或者求出某一策略下的价值函数(预测)。这两种方法都是基于采样的数据来更新的,直接使用和环境交互的过程中采样到的数据来学习。
强化学习的任务
预测(Prediction),在MDP中也叫策略评估(Policy Evaluation),即给定一个策略之后对此策略下的状态价值函数的预测。(求解MRP的状态价值函数也是Prediction)。在求解MDP预测问题上有各种方法,动态规划算法的策略评估(需是known MDP问题)、蒙特卡洛方法采样求解、时序差分算法(TD)采样求解等。动态规划算法需要是白盒环境(known MDP),其他方法都是针对黑盒环境(unknown MDP)。
控制(Control),即算出MDP的最优策略及最优策略下的状态价值函数。在求解MDP控制问题上有各种方法,动态规划算法的策略迭代和价值迭代(需是known MDP问题)、时序差分算法(TD)(SARSA和Q-learning)等。动态规划算法需要是白盒环境(known MDP),其他方法都是针对黑盒环境(unknown MDP)。
强化学习的三种方法
- 基于价值(value-based)
- 基于策略(policy-based)
- 基于模型(model-based)
逆强化学习(Inverse RL)
基于价值:需要找的是每个状态的价值函数, 每次采取的行动,它会采取函数值最大的那个行动
基于策略:需要找的是每个状态下的动作分布,每次采取的行动,来自函数的最大动作概率
状态价值函数(state-value function): V(s) = E[Gt|St=s]
动作价值函数(action-value function): Q(s,a) = E[Gt|St=s, At=a]
一 强化学习表示
1.1 马尔科夫决策过程(MDP)
强化学习任务通常使用==马尔可夫决策过程(Markov Decision Process,简称MDP)==来描述,
具体而言:机器处在一个环境中,每个状态为机器对当前环境的感知;机器只能通过动作来影响环境,当机器执行一个动作后,会使得环境按某种概率转移到另一个状态;
同时,环境会根据潜在的奖赏函数反馈给机器一个奖赏。
综合而言,强化学习主要包含四个要素:状态、动作、转移概率以及奖赏函数。
————周志华《机器学习》
强化学习可以描述成一个MDP(马尔科夫决策过程),即M = {S,A,P,r,γ,τ},这其中:
S 是状态集;
A 是动作集;
P 是状态转移矩阵;
r : S × A → [ − Rmax , Rmax ] 为实时环境奖励;
γ ∈ [0,1] 为折扣因子;
τ = ( s0 , a1 , s1, a2 , s2 , ⋯ , aT , sT)为一个轨迹序列,描述的是一次完整的交互过程(即一个Episode,这个词后面会经常用,相应的( s0 , a1 , s 1)就可以看作一个Step)。
R(τ):一次强化学习的收益, τ本身是一个随机变量,则R(τ)也是一个随机值,优化过程无法对随机值取最大,但我们可以对其期望取最大,即通过不断优化maxπ ∫ R (τ) Pπ(τ) d τ,最终找到最优决策序列。
1.2 关键要素
强化学习关键要素:agent(智能体),reward(奖励),action(行为),state(状态),environment(环境)。
- agent:主要涉及到:策略(Policy),价值函数(Value Function)和模型(Model)。
Policy,可以理解为行动指南,让agent执行什么动作,在数学上可以理解为从状态state到动作action的映射,可分为确定性策略(Deterministic policy)和随机性策略(Stochastic policy),前者是指在某特定状态下执行某个特定动作,后者是根据概率来执行某个动作。
Value Function,对未来总Reward的一个预测。
Model,一个对环境的认知框架,可以预测采取动作后的下一个状态是什么,很多情况下是没有模型的,agent只能通过与环境互动来提升策略。- state:可以细分为三种,Environment State,Agent State和Information State。
Environment State是agent所处环境包含的信息,简单理解就是很多特征数据,也包含了无用的数据。
Agent State是输入给agent的信息,也就是特征数据。
Information State是一个概念,即当前状态包含了对未来预测所需要的有用信息,过去信息对未来预测不重要,该状态就满足马尔科夫性(Markov Property)。Environment State,Agent State都可以是Markov Property。- environment:可以分为完全可观测环境(Fully Observable Environment)和部分可观测环境(Partially Observable Environment)。Fully Observable Environment就是agent了解了整个环境,显然是一个理想情况。
Partially Observable Environment是agent了解部分环境的情况,剩下的需要靠agent去探索。
- S(State) = 环境, 例如迷宫的每一格是一个state, st,表示环境每一步的状态
- A(Actions) = 动作, 在每个状态下。有什么行动是允许的,例如迷宫中行走的方向{上,下,左,右},可表示为at
- R(Rewards) = 奖励, 进入每个状态时,能带来正面或负面的价值。环境奖励rt
- P(Policy) = 方案。由一个状态->行动的函数。
- 策略 π, Agent根据环境状态s,选择动作a的条件概率,可表示为:π (a∣s) = P (at=a ∣ st=s)
- 状态转移概率 Pss′a:当状态为s时,如果执行了a动作,则状态变为s’ 的概率
- 累积回报 G: Gt=rt+1+ γ rt+2 + …… +γn-1rt+n
- 状态价值函数 vπ ( s ) :累积回报的均值表示为我们的状态价值vπ ( s ) = Eπ(Gt|st=s)
- 状态-行为值函数 qπ ( s , a ) 对上述状态和行为对进行评估qπ ( s , a ) = Eπ(Gt|st=s, at=a)
- (S,A,R)是使用者设定的,P是算法自动计算出来的
强化学习算法按照agent分类,可以分为下面几类:
- 关注最优策略(Policy based)
- 关注最优奖励总和(Value based)
- 关注每一步的最优行动(Action based)
根据状态转移概率p(或状态转移矩阵P)是否已知,强化学习可以分为两个大类,即
- Model-Based(基于模型,p已知)和Model-Free(无模型,p未知)
二 值函数
2.1 价值函数
基于价值 (Value-Based)这种方法,目标是优化价值函数V(s)。
价值函数会告诉我们,智能体在每个状态里得出的未来奖励最大预期 (maximum expected future reward) 。
一个状态下的函数值,是智能体可以预期的未来奖励积累总值,从当前状态开始算。
智能体要用这个价值函数来决定,每一步要选择哪个行动。它会采取函数值最大的那个行动。





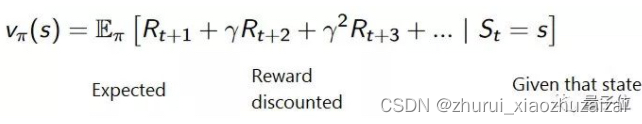
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4488
4488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








