一: 一些基本概念
1.1 信息量:特定事件所携带的信息多少
信息量衡量的是特定事件所携带的信息多少,其数学定义为:其中p(x)是事件x发生的概率。
核心思想:越罕见的事件,其携带的信息量越大;越常见的事件,其携带的信息量越小。
例如:
- 如果某事件必然发生(p(x)=1),信息量为0,意味着观察到它不会带来任何新信息
-如果某事件极其罕见(p(x)很小),信息量很大,观察到它提供了大量信息
1.2 惊奇度:观察到某事件时的"意外程度"
惊奇度表示观察到某事件时的"意外程度",其数学定义为:
核心思想:越意外的事件惊奇度越高,越预期的事件惊奇度越低。
实际上,惊奇度和信息量是完全等价的数学表达式:
信息量强调的是事件所携带的信息内容
惊奇度强调的是事件发生的意外程度
1.3 熵 Entropy:度量随机变量的不确定性
信息论中的基本概念,用于度量随机变量(一个概率分布)的不确定性。
熵的概念可以从信息论角度推导:
- 定义信息量: 对于概率为 p 的事件,其信息量为 I( p )=-log2 ( p)
- 低概率事件携带更多信息(更"意外")
- 高概率事件携带更少信息(更"预期")
1.3.1 定义:熵是平均信息量
熵是平均信息量:
对于离散随机变量X,其熵定义为:
对于一个特例,p(X=x₀)=1,即随机变量 X 确定性地取值为 x₀,我们可以如下推导:





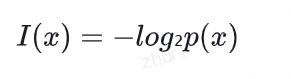
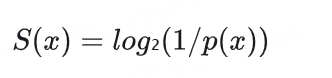
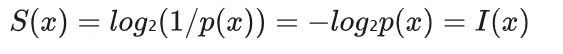
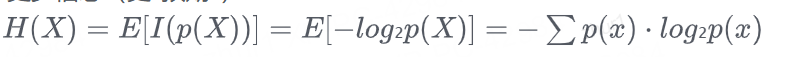
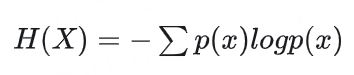
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1016
1016

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








