NER —— BiLSTM+CRF

BiLSTM+CRF

注：
1、以下所有内容均非原创，是集合几篇内容不错的资料集中整理的，含理论讲解、公式推导、代码结合等多个过程，重在讲解 CRF 相关知识点。
2、CSDN 使用 Katex 渲染公式，部分语法可能有问题，{align*} 改用 {aligned} ，背景颜色 \bbox[color][contenc] 改 \colorbox{#e1ffc1}{$ \frac{1}{2} $} ¹²

BiLSTM + CRF 在 NER 领域中被广泛使用，尤其是 BERT 诞生以前，因此该模型可作为 baseline 模型去尝试。

1、原理讲解

1.1 LSTM

LSTM 原理比较简单，参考下图：

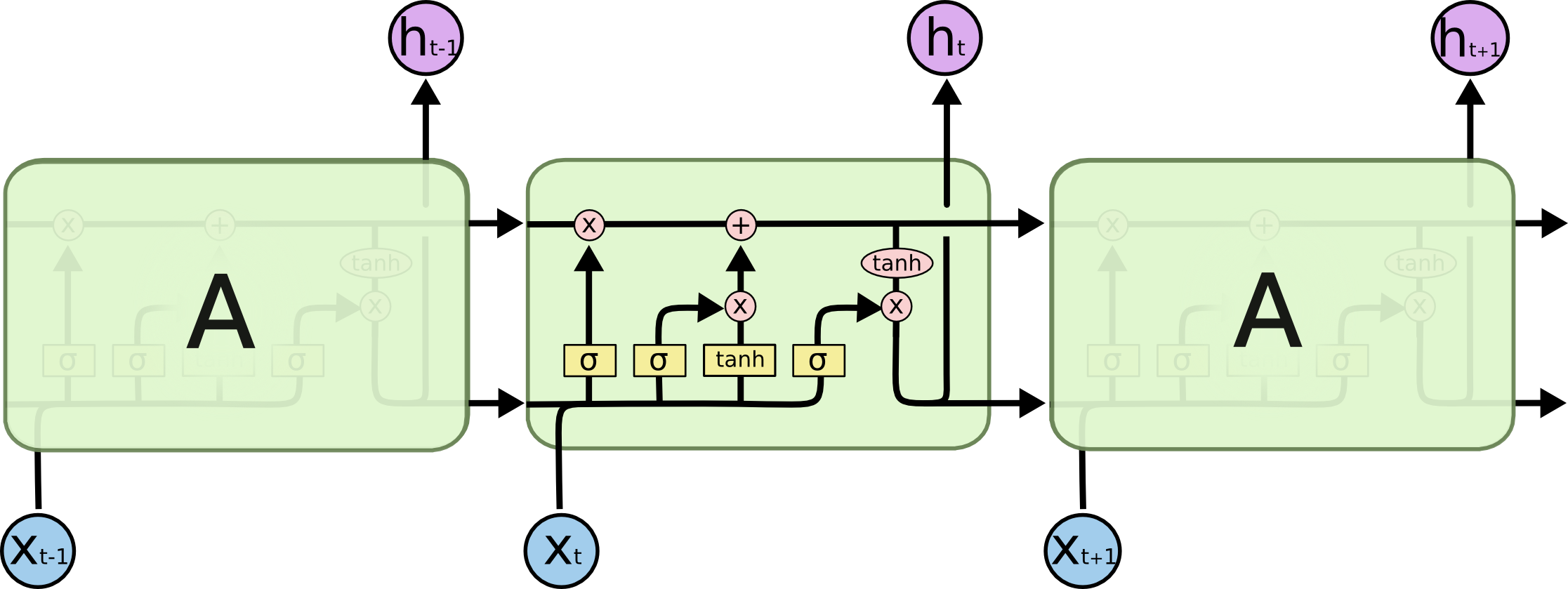
涉及到的主要计算过程为：

$$\begin{array}{l}\\ i_t=\sigma (W_{ii}{x}_t+b_{ii}+W_{hi}{h}_{t-1}+b_{hi})\\ f_t=\sigma (W_{if}{x}_t+b_{if}+W_{hf}{h}_{t-1}+b_{hf})\\ g_t=\tanh (W_{ig}{x}_t+b_{ig}+W_{hg}{h}_{t-1}+b_{hg})\\ o_t=\sigma (W_{io}{x}_t+b_{io}+W_{ho}{h}_{t-1}+b_{ho})\\ c_t=f_t\odot c_{t-1}+i_t\odot g_t\\ h_t=o_t\odot \tanh (c_t)\end{array}$$

各个步骤的具体计算过程及图解如下所示：

关于 LSTM 的更多内容可参考 colah 的博客³。

1.2 BiLSTM

BILSTM 即 双向 LSTM，一般结构如下图所示：

BiLSTM 实际上只是将两个独立的 LSTM 放在一起。对于一个 LSTM，按正常时序进行处理，另一个 LSTM 则按反向时序处理。输出的结果通常采用的是拼接(concat)，而不是求和。即上图中的 $y=[A|A^{\prime }]$。

需要注意的是，拼接的过程是正向的第一个时序与反向的最后一个时序进行拼接，依次类推。

1.3 CRF

条件随机场(crf) 在序列标注任务中被广泛使用，但其涉及的概率知识让很多人望而却步，因此下面将通过一个 demo 示例，详解整个过程⁴:

例如，我们有一句话 $x$，包含 5 个字，$w_0,w_1,w_2,w_3,w_4$，其中 [$w_0$, $w_1$] 是一个”人名”实体，[$w_3$] 是一个“组织”实体，则整个语料我们可标注为 “B-Person I-Person O B-Organization O”。

如上图所示，这就是我们整个 BiLSTM + CRF 的架构图以及 CRF 输出层内容，通过选择概率最大的选项输出最终结果。那么问题来了，BiLSTM 的输出层不也是标签序列嘛，为什么还需要 CRF，直接 argmax BiLSTM 的输出层不行嘛？就像下图这样：

BiLSTM 的输出层也是每种标签的概率输出值，通过选择最大值，也可以做出正确的结果（如图中红色标注），然而事情并非总是如此，更多的时候，得到的是下面的情形：

显而易见，“I-Organization I-Person” 是无效的，至少我们不允许一个实体的标注以 “I” 开头，也不能两个实体的 “I” 连续出现，也就是说我们需要对输出结果强加一些约束条件，这些约束可能是：

• 句子中第一个词的标签应该以 “B-” 或者 “O” 开头，不能是 “I-”
• “B-label1 I-label2 I-label3 I-…” ，在这个模式中，label1,label2,label3… 应该是同一个命名实体的标签。例如，“B-Person I-Person”是有效的，但是“B-Person I-Organization”是无效的。
• “O I-label” 是无效的。一个命名实体的第一个标签应以“B-”开头，而不能是“I-”，换句话说，“O B-label”模式是有效的。
• …

要理解 CRF 的工作原理，我们需要掌握两个分数：散发(Emission) 分数和转移(Transition) 分数。

1.3.1 Emission Score

Emission Score 来自于 BiLSTM 的输出，例如上图中，$w_0$ 被预测为 “B-Person” 的概率为 1.5。为了方便，我们把标签标上序号，{0: “B-Person”, 1: “I-Person”, 2: “B-Organization”, 3: “I-Organization”, 4:“O”}。

我们用 $x_{i,y_j}$ 来表示 Emission Score，其中 $i$ 是词在句子中的序号，$y_j$ 是标签的索引。例如 $x_{i=1,y_j=2}=x_{w_1,B-Organization}=0.1$，即 $w_1$ 的标签被预测为 “B-Organization” 的概率是 0.1.

1.3.2 Transition 分数

我们使用 $t_{y_i{y}_j}$ 表示一个转移分数。例如 $t_{B-Person,I-Person}=0.9$ 意味着标签 $B-Person\to I-Person$ 是 0.9. 因此，我们有一个转移分数矩阵，存储了任意两个标签之间转移的全部分数。

为了是转移矩阵更加强健，我们增加了两个标签，START 和 END。 START 意味着一个句子的开始，但不是第一个词。END 意味着一个句子结束了。

这有一个转移矩阵的例子，这里面包含了 START 和 END 这两个额外的标签。

	START	B-Person	I-Person	B-Organization	I-Organization	O	END
START	0	0.8	0.007	0.7	0.0008	0.9	0.08
B-Person	0	0.6	0.9	0.2	0.0006	0.6	0.008
I-Person	-1	0.5	0.53	0.55	0.0003	0.85	0.08
B-Organization	0.9	0.5	0.0003	0.25	0.8	0.77	0.006
I-Organization	-0.9	0.45	0.007	0.7	0.65	0.76	0.2
O	0	0.65	0.0007	0.7	0.0008	0.9	0.08
END	0	0	0	0	0	0	0

如上表所示，我们可以发现转移矩阵学到了一些有用的约束。

• 句子中第一个词的标签应该以 “B-” 或者 “O” 开头，不能是 “I-” （从“START”转移到“I-Person 或 I-Organization”的转移分数很低）
• “B-label1 I-label2 I-label3 I-…” ，在这个模式中，label1,label2,label3… 应该是同一个命名实体的标签。例如，“B-Person I-Person”是有效的，但是“B-Person I-Organization”是无效的。（例如，从“B-Organization”到“I-Person”的分数仅有0.0003，比转移到其他标签低很多）
• “O I-label” 是无效的。一个命名实体的第一个标签应以“B-”开头，而不能是“I-”，换句话说，“O B-label”模式是有效的。（再一次。例如，tO,I−PersontO,I−Person 的分数很低）
• …

关于这个转移矩阵，你可能会有一个问题这个转移矩阵从哪里怎么得到的呢？

实际上，这个矩阵是 BiLSTM-CRF 模型的一个参数。在你训练你的模型之前，你应该随机初始化所有的转移分数。在训练过程中，这些随机的分数会自动被更新。换句话说，CRF 层可以自动学习这些约束。我们不需要手工构建这个矩阵。这个分数随着训练迭代增加会越来越合理。

1.3.3 CRF loss

CRF 损失函数由两部分组成，真实路径的分数和所有路径的总分数。真实路径的分数应该是所有路径中分数最高的。例如我们有标签类别：{0: “B-Person”, 1: “I-Person”, 2: “B-Organization”, 3: “I-Organization”, 4:“O”, 5: “START”, 6: “END”}

一个包含 5 个字的句子，其可能的标签序列如下：

• 1. START B-Person B-Person B-Person B-Person B-Person END
• 2. START B-Person I-Person B-Person B-Person B-Person END
• ……
• 10. START B-Person I-Person O B-Organization O END
• N. O O O O O O O

假设，每种可能的路径有一个分数 $p_i$，总共有 $N$ 种可能的路径，所有路径的总分数是 $P_{total}=P_1+P_2+\dots +P_N=e^{S_1}+e^{S_2}+\dots +e^{S_N}$ ,其中 $e$ 为自然底数，$S_i=EmissionScore+TransitionScore$

如果我们说第 10 个路径是真实路径，换句话说，第 10 个路径是我们训练数据集的标注标签。则分数 $P_{10}$ 在所有可能路径中应该具有最高的百分比。

下面给出一个损失函数的定义，在训练过程中，BiLSTM-CRF 模型的参数值会被一次次的更新，使得真实路径的分数越来越高。

$$LossFunction=-\frac{P_{RealPath}}{P_1+P_2+\dots +P_N}$$

注：英文版原文中此处没有加负号，而是在后面引入负号，我觉得此处应该加入负号，既然是损失函数，自然是期望分值越小越好。

现在有一些问题：

• 一个路径的分数是如何定义的？
• 如何计算所有可能路径的总分数呢？
• 当我们计算出总分数时，我们需要列举出所有可能的路径吗？（这个问题的答案是 NO）

我们先计算 $S_i$ ，以真实路径 “START B-Person I-Person O B-Organization O END” 为例，

计算 Emission score

$$EmissionScore=x_{0,START}+x_{1,B-Person}+x_{2,I-Person}+x_{3,O}+x_{4,B-Organization}+x_{5,O}+x_{6,END}$$

• 如果第 $index$个单词被标记为 $label$，则分数为 $x_{index,label}$
• 具体的每一项的分数来自于 Bi-LSTM 的输出
• 对于 $x_{0,START}$ 和 $x_{6,END}$ 我们可以将它们设置为 0

计算 Transition score

$$TransitionScore=t_{START\to B-Person}+t_{B-Person\to I-Person}+t_{I-Person\to O}+t_{0\to B-Organization}+t_{B-Organization\to O}+t_{O\to END}$$

• $t_{label1\to label2}$ 是从 $label1$ 转移到 $label2$ 的转移分数
• 这个分数来自 CRF 层。换句话说，这些转移分数实际上是 CRF 层的参数

有了这些基础操作，我们就可以计算 $S_i$ 以及路径分数 $e^{S_i}$，接下来就是计算所有可能路径的所有分数，一猜你就要说枚举所有的挨个计算，这种方式理论上肯定算得出，但计算量多大，效率非常低。

下面的内容计算内容较多，我们放到附录部分，不在此继续展开。

1.3.4 推理

对一条数据进行实体类型预测，该过程比较常用的算法有维特比算法，因涉及的计算量较大，我们将其 放到附录部分。

2、核心代码⁵⁶

该部分采用 PyTorch 计算框架，与 TensorFlow 相比，PyTorch 是采用动态神经网络计算图的，而 TensorFlow 是静态的，动态最直接的好处是便于 debug，你可以观察每一步的计算变化，就如同常规的 Python 代码调试一般，而 TensorFlow 则不同，你无法直观的 debug 或者 print 一些变量的实际数值，而只是一些静态图结点的抽象描述，如张量维度。这么说的意思并不意味着静态图不如动态图，静态图的好处是只编译一次即可，而动态的需要对每一组实例重新定义计算图。

回顾一下上面的部分，假设我们有序列 $x$，其标签序列为 $y$，我们需要计算：

$$P(y|x)=\frac{\exp (\text{Score}(x,y))}{{\sum }_{y^{\prime }}\exp (\text{Score}(x,y^{\prime }))}$$

其中的 score 是通过定义一些对数运算 $\log {\psi }_i(x,y)$ 来确定：

$$\text{Score}(x,y)=\sum _i\log {\psi }_i(x,y)$$

接下来，我们定义 emission 和 transition 两种 score：

$$\text{Score}(x,y)=\sum _i\log {\psi }_{\text{EMIT}}(y_i\to x_i)+\log {\psi }_{\text{TRANS}}(y_{i-1}\to y_i)$$

---

2.1、CRF 部分整体概览⁷

简化解构如下, 整个计算过程大致包括：

def log_sum_exp(smat): # 模型中经常用到的一种路径运算的实现
    ...

class BiLSTM_CRF(nn.Module):
    def neg_log_likelihood(self, features, lengths, tags):  # 求负对数似然，作为loss
        ...

    def _score_sentence(self, frames, tags):    # 求分子
        ...

    def _forward_alg(self, frames):             # 求分母
        ...

    def _viterbi_decode(self, frames):          # 求最优路径分值和最优路径
        ...

2.2、计算 loss

详见 neg_log_likelihood(features, lengths, tags) 方法：

• 这里的 features 是 LSTM 求出每一个字到每种 tag 的 Emission 分数（注意不是概率，加和不一定等于 1，这里与 HMM 不同）
• 求出指定隐状态路径 tags 对应的分值 gold_score，实际就是求正确路径的得分
• 求出所有路径的分值之和 forward_score
• 最后，两者相减，$-\log (a/b)=-[\log (a)-\log (b)]=\log (b)-\log (a)$

$$P(\text{ tags }\mid \text{ words })\triangleq \frac{\exp (\Psi (\text{ tags, words }))}{{\sum }_{\mathbf{t}\in \text{ AllPath }}\exp (\Psi (\mathbf{t},\text{ words }))}$$

$$\underset{\text{负对数似然，作为 loss}}{\underbrace{-\log P(\text{tags}\mid \text{words})}}=\underset{\text{分母对数}}{\underbrace{\log \left[\sum _{t\in \text{ All }\mathrm{Path}}\exp (\Psi (\mathbf{t},\text{ words }))\right]}}-\underset{\text{分子对数}}{\underbrace{\Psi (\text{tags},\text{words})}}$$

2.3、计算分子部分

详见 _score_sentence() 方法：

定义第 $i$ 个单词为 $w_i$，第 $i$ 个 tag 为 $t_i$，序列长度为 $L$；

定义转移矩阵 $T_{i,j}$ 表示从标签 $i$ 到标签 $j$ 的转移分数，$E_{ij}$ 表示第 $i$ 个词预测为 $j$ 标签的 Emission 分数 ，则：

$$\log (\Psi (\text{tags, words}))\triangleq \left[T_{BOS,t_1}+E_{t_1,w_1}+T_{t_1,t_2}+E_{t_2,w_2}+\cdots +E_{t_L,w_L}\right]+T_{t_L,EOS}$$

定义 $t_0\triangleq \text{BOS}$， $LHS=\left[{\sum }_{i=1}^L{T}_{i_{i-1},t_i}+E_{t_i,w_i}\right]+T_{t_L,EOS}$

2.4、计算分母部分

详见 _forward_alg 前半部分

$$\text{分母对数}=\log \left[\sum _{t\in \text{ All }\mathrm{Path}}\exp (\Psi (\mathbf{t},\text{ words }))\right]$$

计算分母的困难在于 $\text{t}\in \text{All Path}$ 难以穷举，例如，当 len(tags)=5且len(words)=10，则 $t$ 的取值空间是 $5^{10}$，所以实际计算采用的是沿序列（时间轴）做动态规划，具体的递推关系如下：

• 穷举所有长度为 $L-1$ 的路径集合，记做 ${\mathbb{P}}^{L-1}$
• 定义 ${\alpha }_{i,j}\triangleq \log \left[{\sum }_{\mathbf{y}\in {\mathbb{P}}^{i-1}}\exp \left(\Psi \left({\mathbf{w}}_{1\sim i},{\mathbf{y}}_{1\sim i-1},y_i=j\right)\right)\right]$，即 "$i$ 时刻到状态 $j$ 的所有路径分数"的log_sum_exp

因此，我们有：

$$\text{分母对数}=\log \left[\sum _{t\in \text{ AllPath }}\exp (\Psi (\mathbf{t},\text{ words }))\right]$$

$$\text{(展开定义)}==\log \left[\sum _{\mathbf{y}\in {\mathbf{P}}^L}\exp \left(\Psi \left({\mathbf{w}}_{1\sim L},{\mathbf{y}}_{1\sim L}\right)\right)\right]$$

$$\text{(穷举}最后一步隐藏状态j\text{)}=\log \left[{\sum }_{j\in AllTags}\sum _{\mathbf{y}\in {\mathrm{p}}^{L-1}}\exp \left(\Psi \left({\mathbf{w}}_{1\sim L-1},{\mathbf{y}}_{1\sim L-1},w_i,j\right)\right)\right]$$

$$\begin{array}{rl}\text{(带入}\alpha \text{定义)}& =\log \left[\sum _{j\in \text{AllTags}}\exp \left({\alpha }_{L-1,j}\right)\right]\\ & =\text{log\_sum\_exp}\left({\alpha }_{L-1,?}\right)\end{array}$$

至此，我们将待求的”分母对数“转化成了关于 $\alpha$ 向量的 log_sum_exp 形式；只要能动态规划求出 $\alpha$ 向量，问题就得到解决，$\alpha$ 的递推关系如下：

$$\begin{array}{rl}{\alpha }_{i,j}& \triangleq \log \left[\sum _{y\in P^{i-1}}\exp \left(\underset{i\text{时刻到达}j\text{状态}}{\underbrace{\Psi ({\mathbf{w}}_{1\sim i},{\mathbf{f}}_{1\sim i-1},y_i=j)}}\right)\right]\\ & =\log \left[\sum _{y\in p^{i-1}}\exp \left(\underset{i-1\text{时刻到达}j\text{状态}}{\underbrace{\Psi ({\mathbf{w}}_{1\sim i-1},{\mathbf{y}}_{1\sim i-2},y_{i-1}=j^{\prime })}}+\underset{\text{状态转移:}{j}^{\prime }\to j}{\underbrace{T_{j^{\prime },j}}}+\underset{\text{状态发射：}j\to w_i}{\underbrace{E_{j,w_i}}}\right)\right]\\ & =\log \left[\sum _j\exp \left({\alpha }_{i-1,j^{\prime }}+T_{j^{\prime },j}+E_{j,w_i}\right)\right]\\ & \dots \text{(递归定义)}\end{array}$$

$$\text{(递归终止条件)}{\alpha }_{0,j}=\{\begin{array}{ll}\underset{=\log (1)\text{，集中了全部概率}}{\underbrace{0}},& \text{j=BOS}\\ \underset{\text{用来代替}\log (0)=-\infty }{\underbrace{-10000}},& \text{else}\end{array}$$

根据上述推导，观察【单个状态】 ${\alpha }_{i-1,j^{\prime }}\to {\alpha }_{i,j}$ 的递推过程：

• 已知：${\alpha }_{i-1,j^{\prime }}$
• 求：${\alpha }_{i,j}$
• 解：加上 $j^{\prime }\to j$ 的状态转移分和 $j\to w_i$ 的发射分，即 ${\alpha }_{i,j}=\log \left[{\sum }_{j^{\prime }}\exp \left({\alpha }_{i-1,j^{\prime }}+j_{j^{\prime },j}+E_{j,w_i}\right)\right]$

将上述【单个状态】的推导加以概括，得到【矩阵化】写法，以 1 -> 2 时刻为例：

$$\alpha \triangleq \left(\begin{array}{ccccc}{\alpha }_{11}& & {\alpha }_{12}& & {\alpha }_{13}\end{array}\right)\stackrel{\text{第一时刻的状态行向量转置为列向量，然后广播为矩阵}}{⟶}\left(\begin{array}{ccccc}{\alpha }_{11}& & {\alpha }_{11}& & {\alpha }_{11}\\ {\alpha }_{12}& & {\alpha }_{12}& & {\alpha }_{12}\\ {\alpha }_{13}& & {\alpha }_{13}& & {\alpha }_{13}\end{array}\right)$$

$$T\triangleq \left(\begin{array}{ccccc}{T}_{11}& & T_{12}& & T_{13}\\ T_{21}& & T_{22}& & T_{23}\\ T_{31}& & T_{32}& & T_{33}\end{array}\right)\stackrel{\text{正常跟左右两个列/行向量相加，导致它们被广播}}{⟶}\dots \text{T 自己无需变形}$$

$$E\triangleq \left(\begin{array}{ccccc}{E}_{21}& & E_{22}& & E_{23}\end{array}\right)\stackrel{\text{行向量广播}}{⟶}\left(\begin{array}{ccccc}{E}_{21}& & E_{22}& & E_{23}\\ E_{21}& & E_{22}& & E_{23}\\ E_{21}& & E_{22}& & E_{23}\end{array}\right)$$

$$\begin{array}{rl}\text{(三者广播相加)}\alpha +T+E& =\left(\begin{array}{lll}{\alpha }_{11}+T_{11}+E_{21}& {\alpha }_{11}+T_{12}+E_{22}& a_{11}+T_{13}+E_{23}\\ {\alpha }_{12}+T_{21}+E_{21}& {\alpha }_{12}+T_{22}+E_{22}& a_{12}+T_{23}+E_{23}\\ {\alpha }_{13}+T_{31}+E_{21}& {\alpha }_{13}+T_{32}+E_{22}& a_{13}+T_{33}+E_{23}\end{array}\right)\\ & \text{(对每一列求 log\_sum\_exp，最终得到行向量；以第三列为例)}\\ & =\left(\begin{array}{ccccc}\dots & & \dots & & \log \left[\exp ({\alpha }_{11}+T_{13}+E_{23})+\exp ({\alpha }_{12}+T_{23}+E_{23})+\dots \right]\end{array}\right)\\ & \triangleq \text{第2时刻的新}\alpha =\left(\begin{array}{ccccc}{\alpha }_{21}& & {\alpha }_{22}& & {\alpha }_{23}\end{array}\right)\end{array}$$

后半部分实际做的与 log_sum_exp 完全一致，只不过便于理解，将各个步骤拆分

经过上面一顿折腾，在计算 $\alpha +T+E$ 之后，我们得到一个 DP 状态矩阵，我们下面称之为 smat，下面我们以一个具体的小示例解释这个过程，假设我们有：

$$smat=\alpha +T+E=\left[\begin{array}{ccccc}1& & 3& & 9\\ 2& & 9& & 1\\ 3& & 4& & 7\end{array}\right]$$

smat[i][j] 表示从状态 $i$ 到 状态 $j$ 的分数，下面我们针对每一列求 log_sum_exp ，意义是求取当前时间步下到各个状态下的分值（综合所有来源），例如 smat[:,2]=[9,1,7]，表示当前时间步下到达状态”2“有三种可能的来源，分别来自上一步的状态 ”0，1，2“，计算结果为： $\text{log\_sum\_exp}(9,1,7)=\log \left[\exp (9)+\exp (1)+\exp (7)\right]=3.964$，这意味着综合所有可能的来源路径，当前时刻能到状态 ”2“ 的分值是 3.964，前两列的计算过程同理可得。

值得注意的是，实际计算过程中采用了一点数学技巧，目的是避免数值上溢。例如，假设 smat[:,2]=[1,999,4]，则：
$$\begin{array}{rlr}\text{log\_sum\_exp}(1,999,4)& =\log (\exp (1)+\exp (999)+\exp (4))& \text{直接计算会遭遇 exp(999) = INF 上溢问题}\\ & =\log (\exp (1-999)\exp (999)+\exp (999-999)\exp (999)+\exp (4-999)\exp (999))& \text{每个元素先乘后除 exp(999)}\\ & =\log ([\exp (1-999)+\exp (999-999)+\exp (4-999)]\ast \exp (999))& \text{提取公因式 exp(999)}\\ & =\log ([\exp (1-999)+\exp (999-999)+\exp (4-999)])+\log (\exp (999))& log乘法拆解成加法\\ & =\log ([\exp (1-999)+\exp (999-999)+\exp (4-999)])+999& \text{此处exp(?)内部都是非正数，不会发生上溢}\\ & =\log ([\exp (smat[0]-vmax)+\exp (smat[1]-vmax)+\exp (smat[2]-vmax)])+vmax& \text{符号化表达}\end{array}$$

2.5 维特比解码

详见 _viterbi_decode()

大部分其实与上一部分相似，但是除了迭代更新 $\alpha$ 以外，还要跟踪每一个时间步上每一个状态的最优”上一步“来自哪里。

附录

计算所有路径的总分

在前面我们定义我们的损失函数为 $LossFunction=-\frac{P_{RealPath}}{P_1+P_2+\dots +P_N}$，我们对其求 log，即
$$\begin{array}{rl}LogLossFunction& =-\log \frac{P_{RealPath}}{P_1+P_2+\dots +P_N}\\ & =-\log \frac{e^{S_{RealPath}}}{e^{S_1}+e^{S_2}+\dots +e^{S_N}}\\ & =-\left(\log \left(e^{S_{RealPath}}\right)-\log \left(e^{S_1}+e^{S_2}+\dots +e^{S_N}\right)\right)\\ & ==-\left(S_{RealPath}-\log \left(e^{S_1}+e^{S_2}+\dots +e^{S_N}\right)\right)\\ & =-\left(\sum _{i=1}^N{x}_{i{y}_i}+\sum _{i=1}^{N-1}{t}_{y_i{y}_{i+1}}-\log \left(e^{S_1}+e^{S_2}+\dots +e^{S_N}\right)\right)\end{array}$$
在前面的章节中，我们已经知道了如何计算真实路径的分数，现在我们需要发现一个有效的方式计算 $\log (e^{S_1}+e^{S_2}+\dots +e^{S_N})$

为了简单化，我们假设仅通过一个长度为 3 的句子进行训练：$\mathbf{x}=[w_0,w_1,w_2]$,此外，在我们的数据集中有两个标签： L a b e l S e t = { l 1 , l 2 } LabelSet = \{l_1,l_2\} LabelSet={l1​,l2​}

我们从 Bi-LSTM 层的输出中获得了散发**分数，如下表所示：

	$l_1$	$l_2$
$w_0$	$x_{01}$	$x_{02}$
$w_1$	$x_{11}$	$x_{12}$
$w_2$	$x_{21}$	$x_{22}$

$x_{ij}$ 表示的是 $w_i$ 的标签是 $l_j$。

此外，CRF 层的转移分数如下表所示：

	$l_1$	$l_2$
$l_1$	$t_{11}$	$t_{12}$
$l_2$	$t_{21}$	$t_{22}$

$t_{ij}$ 表示的是从标签 $i$ 到 $j$ 的转移分数。

接下来，我们的计算目标是：$\log (e^{S_1}+e^{S_2}+\dots +e^{S_N})$.

这是一个分数累加的过程。这个想法与动态规划相似。简而言之，首先可以计算 $w_0$ 的所有可能路径的总分数，然后再计算 $w_0\to w_1$ 的总分数，最后，我们使用最新的总分数计算 $w_0\to w_1\to w_2$。最后的这个总分数就是我们需要的。

在下面的步骤中，我们将看到两个变量：obs 和 previous。previous存储前面步骤中的最后结果。obs标记从当前词中得到的信息。

---

$w_0$:

$obs=[x_{01},x_{02}]$

$previous=None$

如果我们的句子中只有一个单词 $w_0$。我们从前面的步骤中没有得到任何结果，因此 $previous$ 是 None。此外，我们只能通过 $obs=[x_{01},x_{02}]$ 计算第一个词。 $x_{01}$ 和 $x_{02}$ 是上面提到的散发分数。

你可能在想，对于 $w_0$ 的所有可能路径的总分数是多少？这个答案是非常简单的：

$TotalScore(w_0)=\log (e^{x_{01}}+e^{x_{02}})$

---

$w_0$ → $w_1$:

$obs=[x_{11},x_{12}]$

$previous=[x_{01},x_{02}]$

• 把 previous 扩张一下：$$previous=\left(\begin{array}{cc}{x}_{01}& x_{01}\\ x_{02}& x_{02}\end{array}\right)$$
• 把 obs 扩张一下：$$obs=\left(\begin{array}{cc}{x}_{11}& x_{12}\\ x_{11}& x_{12}\end{array}\right)$$，扩张 previous 和 obs 为一个矩阵的目的是因为这样计算更高效。
• 对 $previous$, $obs$ 和转移分数求和：
  $$scores=\left(\begin{array}{cc}{x}_{01}& x_{01}\\ x_{02}& x_{02}\end{array}\right)+\left(\begin{array}{cc}{x}_{11}& x_{12}\\ x_{11}& x_{12}\end{array}\right)+\left(\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right)$$
• $$scores=\left(\begin{array}{cc}{x}_{01}+x_{11}+t_{11}& x_{01}+x_{12}+t_{12}\\ x_{02}+x_{11}+t_{21}& x_{02}+x_{12}+t_{22}\end{array}\right)$$
• 在下次迭代中修改 previous 的值为：$$previous=[\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}}),\log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})]$$

实际，第二次迭代已经计算完了。如果想知道如何计算从$w_0$ 到 $w_1$ 所有可能路径($labe{l}_1$ → $labe{l}_1$, $labe{l}_1$ → $labe{l}_2$, $labe{l}_2$ → $labe{l}_1$, $labe{l}_2$ → $labe{l}_2$)的总分数，你可以通过下面的公式计算。
$$\begin{array}{rl}TotalScore(w_0\to w_1)& =\log (e^{previous[0]}+e^{previous[1]})\\ & =\log (e^{\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})}+e^{\log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})})\\ & =\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}}+e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})\end{array}$$

实际这就是我们的目标 $\log (e^{S_1}+e^{S_2}+\dots +e^{S_N})$.

在这个等式中：

• $S_1=x_{01}+x_{11}+t_{11}$ ($labe{l}_1\to labe{l}_1$)
• $S_2=x_{02}+x_{11}+t_{21}$ ($labe{l}_2\to labe{l}_1$)
• $S_3=x_{01}+x_{12}+t_{12}$ ($labe{l}_1\to labe{l}_2$)
• $S_4=x_{02}+x_{12}+t_{22}$ ($labe{l}_2\to labe{l}_2$)

---

$w_0$ → $w_1$ → $w_2$:

实际上，这是一个迭代过程，我们会做相同的事情，直到最后一次迭代。
$obs=[x_{21},x_{22}]$

$previous=[\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}}),\log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})]$

• 扩展 previous 为：$$previous=\left(\begin{array}{cc}\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})& \log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})\\ \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})& \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})\end{array}\right)$$

• 扩展 obs 为$$obs=\left(\begin{array}{cc}{x}_{21}& x_{22}\\ x_{21}& x_{22}\end{array}\right)$$

• 对 previous, obs 以及转移分数求和：
  $$scores=\left(\begin{array}{cc}\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})& \log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})\\ \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})& \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})\end{array}\right)+\left(\begin{array}{cc}{x}_{21}& x_{22}\\ x_{21}& x_{22}\end{array}\right)+\left(\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right)$$
  $$scores=\left(\begin{array}{cc}\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})+x_{21}+t_{11}& \log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})+x_{22}+t_{12}\\ \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})+x_{21}+t_{21}& \log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})+x_{22}+t_{22}\end{array}\right)$$

  在下次迭代中修改 previous 的值为：
  $$\begin{array}{rl}previous& =[\log (e^{\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})+x_{21}+t_{11}}+e^{\log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})+x_{21}+t_{21}}),\log (e^{\log (e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})+x_{22}+t_{12}}+e^{\log (e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})+x_{22}+t_{22}})]\\ & =[\log ((e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})e^{x_{21}+t_{11}}+(e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})e^{x_{21}+t_{21}},\log ((e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})e^{x_{22}+t_{12}}+(e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})e^{x_{22}+t_{22}})]\end{array}$$

$$\begin{array}{rl}TotalScore(w_0\to w_1\to w_2)& =\log (e^{previous[0]}+e^{previous[1]})\\ & =\log (e^{\log ((e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})e^{x_{21}+t_{11}}+(e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})e^{x_{21}+t_{21}})}\\ & =\log (e^{\log ((e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})e^{x_{21}+t_{11}}+(e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})e^{x_{21}+t_{21}})}+e^{\log ((e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}})e^{x_{22}+t_{12}}+(e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})e^{x_{22}+t_{22}})})\\ & =\log (e^{x_{01}+x_{11}+t_{11}+x_{21}+t_{11}}+e^{x_{02}+x_{11}+t_{21}+x_{21}+t_{11}}+e^{x_{01}+x_{12}+t_{12}+x_{21}+t_{21}}+e^{x_{02}+x_{12}+t_{22}+x_{21}+t_{21}}+e^{x_{01}+x_{11}+t_{11}+x_{22}+t_{12}}+e^{x_{02}+x_{11}+t_{21}+x_{22}+t_{12}}+e^{x_{01}+x_{12}+t_{12}+x_{22}+t_{22}}+e^{x_{02}+x_{12}+t_{22}+x_{22}+t_{22}})\end{array}$$

我们完成了目标, $\log (e^{S_1}+e^{S_2}+\dots +e^{S_N})$. 在我们的小例子，一个句子中含有三个单词，我们的标签集中有两个标签。因此，共有 8 种可能的路径。

计算推理

同上，我们仍以 3 个字的句子为例，$X=[w_0,w_1,w_2]$ ，而且通过训练后的模型，我们得到了 Emission 矩阵和 Transition 矩阵：

• Emission 矩阵：

	$l_1$	$l_2$
$w_0$	$x_{01}$	$x_{02}$
$w_1$	$x_{11}$	$x_{12}$
$w_2$	$x_{21}$	$x_{22}$

• Transition 矩阵：

	$l_1$	$l_2$
$l_1$	$t_{11}$	$t_{12}$
$l_2$	$t_{21}$	$t_{22}$

再次强调，上述两个表是经过训练阶段训练后的模型参数，尽管形式上与训练阶段计算所有路径总分部分一致

与训练阶段一致，我们仍需 obs 和 previous 两个变量，另外还需要 ${\alpha }_0$ 和 ${\alpha }_1$ 两个新变量，分别用于存储历史最佳分数和历史最佳分数对应的类别索引。预测的顺序依然是从 $w_0$ 开始。

$w_0$:

$obs=[x_{01},x_{02}]$

$previous=None$

这个的计算可以直接通过 Emission 矩阵得到，例如 $obs=[x_{01}=0.2,x_{02}=0.8]$，显然 $w_0$ 的最佳预测结果是 $l_2$。

---

$w_0$ → $w_1$:

$obs=[x_{11},x_{12}]$

$previous=[x_{01},x_{02}]$

用前面的方法我们可以得到 $$scores=\left(\begin{array}{cc}{x}_{01}+x_{11}+t_{11}& x_{01}+x_{12}+t_{12}\\ x_{02}+x_{11}+t_{21}& x_{02}+x_{12}+t_{22}\end{array}\right)$$

重点在于如何更新 $previous$，

$$previous=[\max (scores[00],scores[10]),\max (scores[01],scores[11])]$$

举个例子，例如：$$scores=\left(\begin{array}{cc}{x}_{01}+x_{11}+t_{11}& x_{01}+x_{12}+t_{12}\\ x_{02}+x_{11}+t_{21}& x_{02}+x_{12}+t_{22}\end{array}\right)=\left(\begin{array}{cc}0.2& 0.3\\ 0.5& 0.4\end{array}\right)$$

则：$previous=[\max (scores[00],scores[10]),\max (scores[01],scores[11])]=[0.5,0.4]$

解释一下，我们要预测的是 $w_1$，当 $w_1$ 被预测为 $l_1$ 时，其实一共有两个路径:

• $w_0$ 被预测为 $l_1$（即 $x_{01}$），$l_1$ 下次可以转到 $l_1$（即 $t_{11}$），$w_1$ 被预测为 $l_1$
• $w_0$ 被预测为 $l_2$（即 $x_{02}$），$l_2$ 下次可以转到 $l_1$（即 $t_{21}$），$w_1$ 被预测为 $l_1$

上面两个过程对应的就是 $score{s}_{00}$ 和 $score{s}_{10}$ ，同理，当 $w_1$ 被预测为 $l_2$ 对应的就是 $score{s}_{01}$ 和 $score{s}_{11}$

因此：

• ${\alpha }_0=[(scores[10],scores[11])]=[(0.5,0.4)]$
• ${\alpha }_1=[(ColumnIndex(scores[10]),ColumnIndex(scores[11]))]=[(1,1)]$

上式中，${\alpha }_1$ 最后的 $[(1,1)]$ 表示的是标签的索引，即 $(1,1)=(l_2,l_2)$，即 $(l_2\to l_1)=0.5,(l_2\to l_2)=0.4$

---

$w_0$ → $w_1$ → $w_2$:

$obs=[x_{21},x_{22}]$

$previous=[0.5,0.4]$

计算 scores，并假设计算结果为：

$$scores=\left(\begin{array}{cc}0.5+x_{21}+t_{11}& 0.5+x_{22}+t_{12}\\ 0.4+x_{21}+t_{21}& 0.4+x_{22}+t_{22}\end{array}\right)=\left(\begin{array}{cc}0.6& \underline{0.9}\\ \underline{0.8}& 0.7\end{array}\right)$$

再次更新：

• $previous=[0.8,0.9]$
• ${\alpha }_0=[(0.5,0.4),\underline{(0.8,0.9)}]$
• ${\alpha }_1=[(1,1),\underline{(1,0)}]$

---

预测：

根据 ${\alpha }_0$ 和 ${\alpha }_1$ 我们选择最佳路径，首先是 ${\alpha }_0$ ，最后一个字的标签得分分别是 0.8 和 0.9，我们选择 0.9，也就是最后一个字被预测为 $l_2$，${\alpha }_0$ 中 0.9 的位置对应 ${\alpha }_1$ 中的 0，即前一个字的标签是 $l_1$，继续往前推，前一个个字的标签是 $l_2$。所以预测的最佳路径是 $l_2\to l_1\to l_2$。

---

参考资料：

---

1. latext公式换行对齐\begin{align*}报错 ↩︎

2. How to make a background box around a fraction (“bbox”) with Katex? ↩︎

3. Understanding LSTM Netwoks ↩︎

4. CRF Layer on the Top of BiLSTM 1-8 ↩︎

5. ADVANCED: MAKING DYNAMIC DECISIONS AND THE BI-LSTM CRF ↩︎

6. code: bilstm_crf_pytorch ↩︎

7. 手撕 BiLSTM-CRF ↩︎