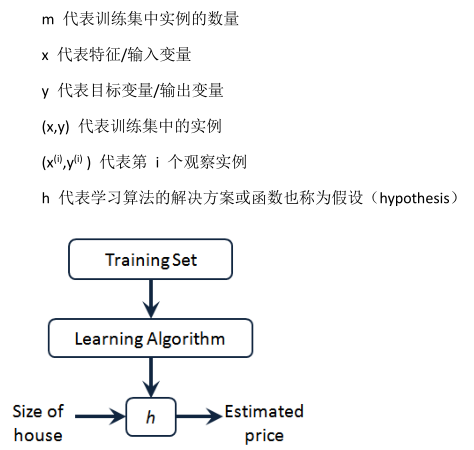
单变量线性回归(Linear Regression with One Variable)
预测器表达式:
选择合适的参数(parameters)θ0 和 θ1,其决定了直线相对于训练集的准确程度。
建模误差(modeling error):训练集中,模型预测值与实际值之间的差距。
目标:选出使建模误差平方和最小的模型参数,即损失函数最小。
损失函数(Cost Function):
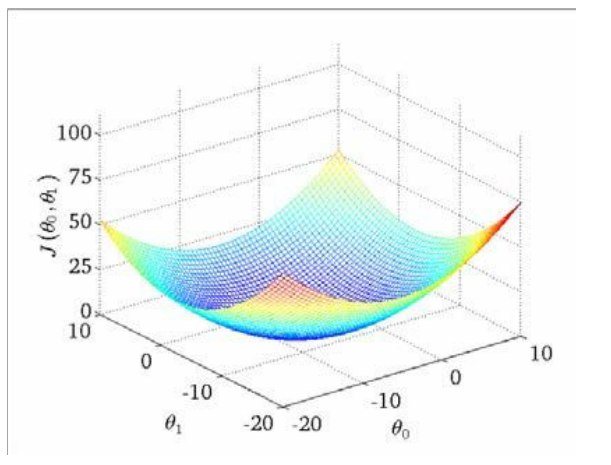
可以看出在三维空间中存在一个使得 J(θ0,θ1)最小的点。
梯度下降算法(Gradient Descent):
批量梯度下降(batch gradient descent)算法的公式为:
总结:
1、先确定预测模型,然后确定损失函数;
2、使用梯度下降算法,让损失函数最小化,此时的参数可使预测模型的经验误差达到最优。
————————————————————————————————————————————————
多变量线性回归(Linear Regression with Multiple Variables)
为了简化公式,引入 x0=1。
此时模型中的参数是一个 n+1 维的向量,任何一个训练实例也都是 n+1 维的向量,特征矩阵 X 的维度是 m*(n+1)。
公式可以简化为:
多变量线性回归代价函数,这个代价函数是所有建模误差的平方和:
多变量线性回归的批量梯度下降算法为:
即:
开始随机选择一系列的参数值, 计算所有的预测结果后, 再给所有的参数一个新的值,如此循环直到收敛。
————————————————————————————————————————————————————————
Feature Scaling
将所有特征的尺度都尽量缩放到-1 到 1 之间。
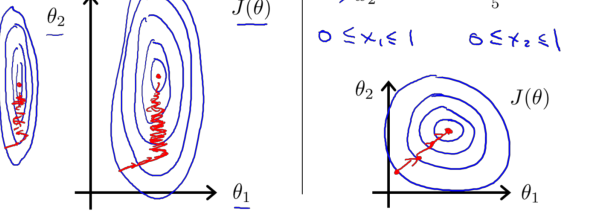
梯度下降算法实践 2——学习率
梯度下降算法的每次迭代受到学习率的影响:
如果学习率 α 过小, 则达到收敛所需的迭代次数会非常高;
如果学习率 α 过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率: α=0.01,0.03,0.1,0.3,1,3,10
————————————————————————————————————————————————————————
多项式回归( Polynomial Regression)
线性回归并不适用于所有数据, 有时需要曲线来适应数据。
比如一个二次方模型:
或者三次方模型:
通常需要先观察数据然后再决定准备尝试怎样的模型。
根据函数图形特性,还可以使用:
注:如果采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
————————————————————————————————————————————————————————
正规方程通过求解下面的方程来找出使得代价函数最小的参数:
假设训练集特征矩阵为 X(包含了 x0=1),训练集结果为向量 y
则利用正规方程解出向量:
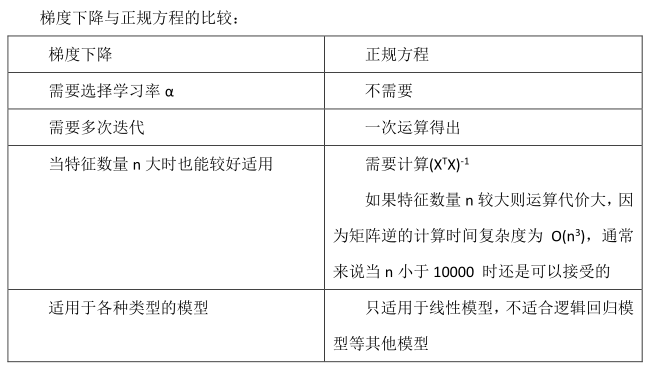
总结:
只要特征变量的数目并不大,标准方程是一个很好的计算参数 θ 的替代方法。
具体地说, 只要特征变量数量小于一万, 通常使用标准方程法, 而不使用梯度下降法。
随着学习算法越来越复杂,例如,分类算法,逻辑回归算法, 并不能使用标准方程法。
对于那些更复杂的学习算法,将仍然使用梯度下降法。
因此,梯度下降法是一个非常有用的算法,可以用在有大量特征变量的线性回归问题。
或者在以后课程中,会讲到的一些其他的算法,因为标准方程法不适合或者不能用在它们上。
但对于这个特定的线性回归模型, 标准方程法是一个比梯度下降法更快的替代算法。
所以,根据具体的问题,以及你的特征变量的数量,这两种算法都是值得学习的。
不可逆性:
X'X 的不可逆的问题很少发生
第一个原因:一个线性方程的两个特征值是线性相关的,矩阵 X'X 不可逆;
第二个原因:用大量的特征值,尝试实践学习算法的时候,可能会导致矩阵 X'X 不可逆。
通常,使用一种叫做正则化的线性代数方法,通过删除某些特征或者是使用某些技术,来解决当 m 比
n 小的时候的问题。即使你有一个相对较小的训练集,也可使用很多的特征来找到很多合适的参数。








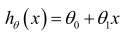
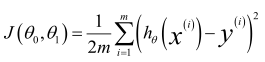
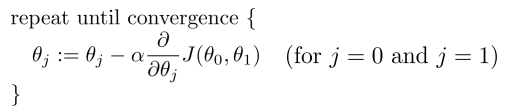
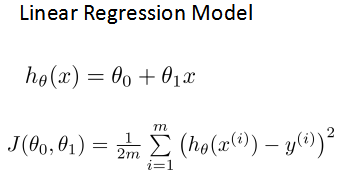


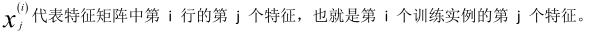
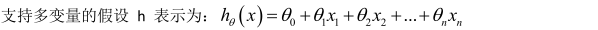
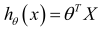
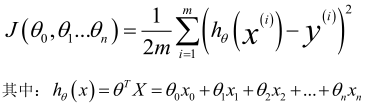

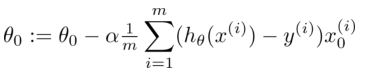
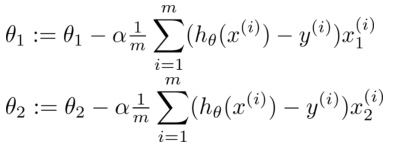
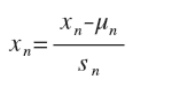

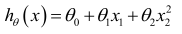
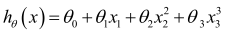
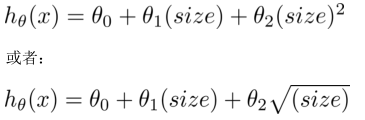
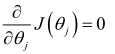
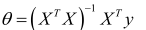
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








