只是为了应个quiz
我们首先说说ICA一般会应用图像降噪、人脸识别、遥感图像分类、去眼电、脑电图等方面,凡是带有隐变量的问题,都是可以尝试使用ICA来解决的。
我们直接上一个盲源分离问题来说明这个ICA:
假设现在有一n个人同时说话,经过了m个时刻,我们记录下信号源:
如果按照时间来标记,我们可以这么写:
其中s1是代表第1的时刻,n个人同时说话的混合。
如果还有n个接收器接收n个人说话,那么同样经过了m个时刻,我们记下观测信号:
同样按照时间来标记,我们可以这么写:
我们将源信号记作S,观测信号记作X,我们可以这么理解:
也就是说在j时刻n个人的说话信号是经过A这么处理合成了xj。
那么我们计算A的逆矩阵W,就可以写成:
此时我们可以将A叫做混合矩阵,W叫做解混矩阵。
那么对于这个问题来说,我们不妨做两点假设:
(1) 源信号之间彼此统计独立
(2) 源信号是非高斯分布
第一个假设还好理解,第二个是什么鬼?
根据中心极限定理,一组有确定方差的独立随机变量的和趋近于高斯分布,也就是说给定随机变量A和B,A+B比A或B更接近高斯分布,那么根据混合信号,如果能够找到一组独立信号,或者说找到一组最不像高斯分布的信号,那么就极有可能是是源信号。
既然如此,我们假定第i个源信号的概率密度函数为pi(s),第j个时刻的n个源信号记作向量sj,则在第j时刻向量sj的联合密度为:
我们根据前边的:
可得:
那么把所有时刻乘到一起,从而得到似然函数:
可以对似然函数取对数得到对数似然:
那么新的目标函数为:
走到这一步,我们发现没办法做了,因为源信号的的概率密度函数未知啊。
既然如此,我们大胆使用Sigmoid函数作为源信号的累计概率函数,从而源信号的概率密度为Sigmoid函数的导函数:
我们再对f(x)求导,得到概率分布函数:
那么现在就可以对wij求导:
其中第二行|W|的导数有专门关于”行列式求导“的公式,这里是直接用结论,将上边的式子写成向量:
既然如此,我们就可以用梯度下降来计算了:
在做ICA的时候,一般要先做中心化、白化、去噪,其实我们觉得看实际情况了,未必说做了白化就要好多少,但是中心化还是要做的,除非有截距。
好了,到此就将ICA介绍完了,欢迎批评指正。












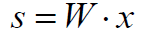




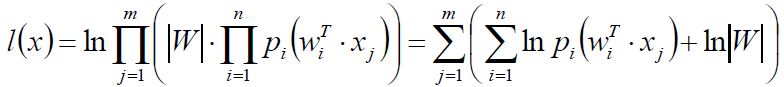
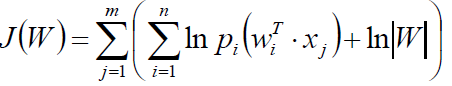
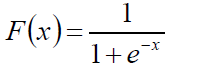
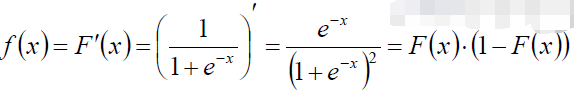
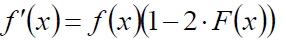
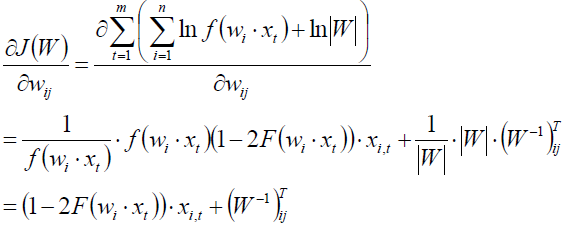

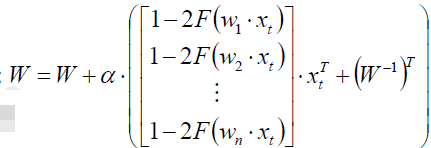














 4241
4241

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








