分类算法：Logistic regression详解与Matlab代码实现

最新推荐文章于 2024-04-21 15:08:24 发布

pandapandapandapan

最新推荐文章于 2024-04-21 15:08:24 发布

阅读量3.4k

点赞数 2

文章标签：机器学习逻辑回归

本文链接：https://blog.csdn.net/weixin_38080060/article/details/107286866

版权

1 模型引入与概述

2 matlab代码实现

3 Logistic regression的多分类

4 总结

1 模型引入与概述

机器学习的第一个算法也是最简单的算法是线性回归，对于输入x，模型输出的y是连续的，这也是回归问题(预测)和分类问题的区别，分类问题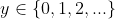 $y\in\left\{0,1,2,...\right\}$ ，二分类问题 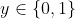$y\in\left\{0,1\right\}$ 都是离散值，而回归问题 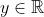$y\in\mathbb{R}$ 。明明是分类算法为什么称作Logistic regression，个人理解是因为Logistic Function的输出是 $\left [ 0,1 \right ]$ 之间的实数，这与回归问题的输出是如出一辙的。

1.1 sigmoid函数

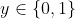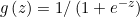下面进行Logistic regression模型的详解，Logistic regression不仅能解决二分类问题，也能处理多分类问题，以二分类问题 $y\in\left\{0,1\right\}$ 为例，多分类问题会在后面讲解。Logistic regression的主要思想是使得目标函数的输出 $h_\theta {\left ( x \right )}\in\left [ 0,1 \right ]$ ，而能够使得函数输出在0，1之间的则关键在于阶跃函数sigmoid function： $g\left ( z \right )=1/\left ( 1+e^{-z} \right )$ ，sigmoid函数的图像如下图所示：从图上可以看出，对于输入值大于零，输出值大于0.5；输入值小于零，输出值小于0.5，这也是用于分类的依据，另外，当输入值接近正无穷大时，函数输出为1，当输入值趋近无穷小时，函数输出为0。

1.2 模型表示

对于Logistic regression模型，具体表示为：

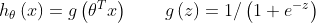$h_{\theta }\left ( x \right )=g\left ( \theta ^{T}x \right )\textbf{} \ \ \ \ \ \ g\left ( z \right )=1/\left ( 1+e^{-z} \right )$ ,

即：

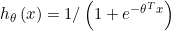
$h_{\theta }\left ( x \right )=1/\left ( 1+e^{-\theta ^{T}x} \right )$

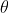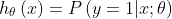模型预测的是对于给定x和参数 ${\color{Blue} }\theta$ ，其输出值为1的概率： $h_{\theta }\left ( x \right )=P\left ( y=1|x;\theta \right )$ ，并且有 $P\left(y=1|x; \theta\right )+P\left(y=0|x; \theta\right )=1$ .

其决策边界表示为：

$y $$\left\{ \begin{array}{c}=1\ \ \ \ \ h_{\theta}\left ( x \right )\geq 0.5 \\ \\=0\ \ \ \ \ h_{\theta }\left ( x \right )< 0.5\end{array}\right. $$$

当 $\theta ^{T}x\geqslant 0\mathbf{}$ 时，模型预测输出的值为1。

下面介绍两个简单的例子便于理解：

(1)线性边界：对于模型 $h_{\theta} \left(x \right) \right )=g\left( \theta_{0}+\theta_{1}x_{1}+\theta_{3}x_{3}\right ) ,\ \ \ \ \theta_{0}=-3\ \ \ \theta_{1}=1\ \ \ \theta_{2}=1$ ，预测y=1，如果 $-3+x_{1}+x_{2}\geq0$ ，即决策边界为 $x_{1}+x_{2}\geq3$

(2)非线性边界：对于模型 $h_\theta\left( x\right )=g\left(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_{1}^2+\theta_4x_{2}^2 \right )$ ， $\theta=[-1,0,0,1,1]^T$ ，即当 $x_1^2+x_2^2-1\geq0$ ，预测输出y=1

1.3 代价函数

Logistic regression模型抽象表示为：给定训练集 $\left \{ \left(x^{\left(1 \right )}, y^{\left(1 \right )}\right),\left(x^{\left(2 \right )}, y^{\left(2 \right )}\right),...\left(x^{\left(m \right )}, y^{\left(m \right )}\right)\right \}$ ， $x\in\left[x_0,x_1,...x_n \right ]^T$ ， $x_0=1$ ， $y\in\left\{0,1\right\}$ ， $h_\theta\left(x \right )=\frac{1}{1+e^{-\theta^Tx }}$ 。

模型的代价函数若用线性回归的形式表示则为 $J\left( \theta\right )=\frac{1}{m} \sum_{i=1}^{m}\frac{1}{2}\left(h_\theta\left(x \right )-y^{\left(i \right )}\right)^2$ ，计算第i个样本的损失即为

$Cost\left(h_\theta\left(x^{\left(i \right )} \right ),y^{\left(i\right)} \right)=\frac{1}{2}\left(h_\theta\left(x^{\left(i \right )} \right )-y^{\left(i \right )} \right )^2$ .

如果将sigmoid函数代入到代价函数，函数为非凸的，有很多的局部最优解，梯度下降法不能保证收敛到全局最小值，因而我们需要重新构造一种代价函数，并且该代价函数能够很好的衡量误差的大小。构造Logistic Regression模型的代价函数为

$Cost\left(h_\theta\left(x \right ),y \right )= \left\{ \begin{array}{c} -log\left(h_\theta\left(x \right ) \right ) \ \ \ \ if \ y=1\\ -log\left(1-h_\theta\left(x \right ) \right ) \ \ \ if \ y=0\end{array}\right. $$$

对于y=1， $h_\theta\left(x \right )\in\left[0,1 \right ]$

当样本标签值为1，而函数预测标签值为0时，此时的损失值极大，体现了惩罚，反之，标签值为1，预测值也为1时，损失值为0.对于y=0的情况同样如此。

1.4 梯度下降法

下面详细介绍模型的损失函数以及梯度下降的求解： $J\left( \theta\right )=\frac{1}{m} \sum_{i=1}^{m}\frac{1}{2}\left(h_\theta\left(x \right )-y^{\left(i \right )}\right)^2$ 损失函数y=0和y=1统一写成 $Cost\left(h_\theta\left(x^{\left(i \right )} \right ),y \right)=-ylog\left(h_\theta\left(x) \right )-\left(1-y \right )log\left(1-h_\theta\left(x) \right )$ ，因而

$J\left( \theta\right )=\frac{1}{m} \sum_{i=1}^{m}Cost\left(h_\theta\left(x^{\left(i \right )} \right ) ,y^{\left(i \right )}\right )\\ \ \ \ =-\frac{1}{m}\left[\sum_{i=1}^{m}y^{\left(i \right )} logh_\theta\left(x^{\left(i \right )} \right ) +\left(1-y^{\left(i \right )} \right ) \left(1-logh_\theta\left(x^{\left(i \right )} \right ) \right )\right ]$

需要最小化损失函数，得到参数 $\theta$ ，梯度下降法为

$repeat\left\{\\\theta_j=\theta_j-\alpha \frac{\partial J\left(\theta \right )}{\partial \theta_i} \right \}_{j=1:m}$ ，

需要注意的是对于每个 $\theta_j$ 的更新应该同步进行，即一次性更新所有的 $\theta_j$ 。

$\frac{\partial J\left(\theta \right )}{\partial \theta_i}=\frac{1}{m}\sum_{i=1}^{m}\left(h_\theta\left(x^{\left(i \right )} \right )-y^{\left(i \right )} \right )x_j^{ \left(i\right) }$

对上式求解的解析如下：

$J\left(\theta \right )=-\frac{1}{m}\left[\sum_{i=1}^{m}y^{\left(i \right )} logh_\theta\left(x^{\left(i \right )} \right ) +\left(1-y^{\left(i \right )} \right ) \left(1-logh_\theta\left(x^{\left(i \right )} \right ) \right )\right ]\\ =-\frac{1}{m}\left[\sum_{i=1}^{m}-y^{\left(i \right )} log\left(1+e^{-\theta*x^{\left(i \right )} } \right )-\left(1-y^{\left(i \right )} \right ) \left(1+e^{-\theta*x^{\left(i \right )} } \right )\right ]\\ =\frac{1}{m}\sum_{i=1}^{m}\left[\left(1-y^{\left(i \right )} \right )*\theta*x^{\left(i \right )}+log\left(1+e^{-\theta*x^{\left(i \right )}} \right ) \right ]$

记中括号里面的式子为A，则有

$$$\frac{\partial A }{\partial\theta_j}=\left(1-y^{\left(i \right )} \right )*x^{\left(i \right )}+\frac{1}{1+e^{-\theta*x^{\left(i \right )}}}*e^{-\theta*x^{\left(i \right )}}*\left(-x^{\left(i \right )} \right )\\ =x^{\left(i \right )}\left(\frac{1}{1+e^{-\theta*x^{\left(i \right )}}} -y^{\left(i \right )}\right )\\ =x^{\left(i \right )}*\left(h_\theta\left(x \right )-y^{\left(i \right )} \right )$

2 matlab代码实现

以代价函数 $J\left(\theta \right )=\left(\theta_1-5 \right )^2+\left(\theta_2-5 \right )^2$ 为例， $\frac{\partial J\left(\theta \right )}{\partial \theta_1}=2*\left(\theta_1-5 \right )$ ， $\frac{\partial J\left(\theta \right )}{\partial \theta_2}=2*\left(\theta_2-5 \right )$

%代价函数
function [jval,gradient]=costFunction(theta)
jval=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);

%主函数
options=optimset('GradObj','on','MaxIter',100);
initialTheta=zeros(2,1);
[optTheta,functionVal,exitFlag]=fminunc(@costFunction,initialTheta,options);

3 Logistic regression的多分类

对于邮件，除了区分是否是垃圾邮件，同样可以对邮件的来源分成工作邮件、朋友邮件、家庭邮件、个人爱好邮件。

如下例的三分类问题，如下图图1所示：

图1 图2 图3

上图图2先将第一类作为一类，其他两类看作相同的另一类，该伪训练集得到的结果是 $P\left(y=1|x;\theta \right )$ ，即预测输出为1的概率，同样上图图2是将第二类作为一类，而剩余两类作为同一类，得到的结果是 $P\left(y=2|x;\theta \right )$ ，即预测输出为2的概率，对于第三类依此类推，最后输出选择概率大的作为分类结果。

4 总结

Logistic regression分类方法思想简单，易于实现，不管是二分类还是多分类，都能用此模型完成，它的本质是预测某个样本所属于某标签的概率，其关键在于代价函数的构造，既能体现惩罚，又能与模型结果相契合，妙哉！(第一次写博客，感受到了前辈们写博客的辛苦，万事开头难，有不足之处希望能够在后期改正，保持认真对待的态度)

pandapandapandapan

关注

2
点赞
踩
15

收藏

觉得还不错? 一键收藏
0
评论
分类算法：Logistic regression详解与Matlab代码实现

机器学习的第一个算法也是最简单的算法是线性回归，对于输入x，模型输出的y是连续的，这也是回归问题(预测)和分类问题的区别，分类问题，二分类问题都是离散值，而回归问题。而对于为什么明明是分类算法却称作Logistic regression，个人理解是因为Logistic Function的输出是之间的实数，这与回归问题是如出一辙的。下面进行Logistic regression模型的详解，Logistic regression不仅能解决二分类问题，也能处理多分类问题，以二分类问题为例，多分类问题会在后面讲
复制链接

扫一扫