文章目录
连续函数是数学分析的核心概念,其性质是理解微积分的关键。本文将结合Python可视化,从基本概念到重要性质,系统讲解连续函数的特性,并通过丰富的代码示例帮助读者建立直观理解。
一、连续函数基本概念回顾
连续性描述的是函数在某一点附近的光滑行为。从几何角度看,连续函数的图像是一条"连绵不断"的曲线,笔不离纸就能画出。
1.1 连续性的严格定义
数学定义:函数 f ( x ) f(x) f(x) 在点 x 0 x_0 x0 处连续,当且仅当满足:
- 在 x 0 x_0 x0 处有定义( f ( x 0 ) f(x_0) f(x0) 存在)
- lim x → x 0 f ( x ) \lim \limits_{x \to x_0} f(x) x→x0limf(x) 存在
- lim x → x 0 f ( x ) = f ( x 0 ) \lim \limits_{x \to x_0} f(x) = f(x_0) x→x0limf(x)=f(x0)
用ε-δ语言表述:对任意 ε > 0 \varepsilon > 0 ε>0,存在 δ > 0 \delta > 0 δ>0,使得当 ∣ x − x 0 ∣ < δ |x - x_0| < \delta ∣x−x0∣<δ 时,有 ∣ f ( x ) − f ( x 0 ) ∣ < ε |f(x) - f(x_0)| < \varepsilon ∣f(x)−f(x0)∣<ε。
手动求解步骤: 对于函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2 在 x 0 = 2 x_0 = 2 x0=2 处的连续性证明:
- f ( 2 ) = 4 f(2) = 4 f(2)=4,函数在 x = 2 x=2 x=2有定义
- lim x → 2 x 2 = 4 \lim \limits_{x \to 2} x^2 = 4 x→2limx2=4,极限存在
- lim x → 2 x 2 = 4 = f ( 2 ) \lim \limits_{x \to 2} x^2 = 4 = f(2) x→2limx2=4=f(2),满足连续性条件
Python代码:
import matplotlib.pyplot as plt
import numpy as np
# 设置支持 Unicode 的字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei','DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 连续性的ε-δ演示
def demonstrate_continuity():
# 示例函数:f(x) = x^2 在 x=2 处的连续性
def f(x):
return x**2
x0 = 2
f_x0 = f(x0)
epsilon = 0.5
# 计算对应的delta
# 对于f(x)=x^2,|f(x)-f(2)| = |x^2-4| = |x-2||x+2|
# 当|x-2|<1时,|x+2|<5,所以取delta = min(1, epsilon/5)
delta = min(1, epsilon/5)
x_values = np.linspace(x0 - 2*delta, x0 + 2*delta, 100)
y_values = f(x_values)
plt.figure(figsize=(10, 6))
plt.plot(x_values, y_values, 'b-', linewidth=2, label='f(x) = x²')
plt.axvline(x=x0, color='r', linestyle='--', alpha=0.7, label=f'x_0 = {x0}')
plt.axhline(y=f_x0, color='r', linestyle='--', alpha=0.7, label=f'f(x_0) = {f_x0}')
# 显示ε区间
plt.axhline(y=f_x0 + epsilon, color='g', linestyle=':', alpha=0.5, label='ε区间')
plt.axhline(y=f_x0 - epsilon, color='g', linestyle=':', alpha=0.5)
plt.fill_between(x_values, f_x0 - epsilon, f_x0 + epsilon, alpha=0.1, color='green')
# 显示δ区间
plt.axvline(x=x0 + delta, color='orange', linestyle=':', alpha=0.5, label='δ区间')
plt.axvline(x=x0 - delta, color='orange', linestyle=':', alpha=0.5)
plt.fill_betweenx(y_values, x0 - delta, x0 + delta, alpha=0.1, color='orange')
plt.scatter([x0], [f_x0], color='red', s=50, zorder=5)
plt.title('函数连续性演示: ε-δ定义')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print(f"对于 ε = {epsilon}, 找到 δ = {delta:.3f}")
print(f"当 |x - {x0}| < {delta:.3f} 时,|f(x) - {f_x0}| < {epsilon}")
demonstrate_continuity()
Python代码执行结果:
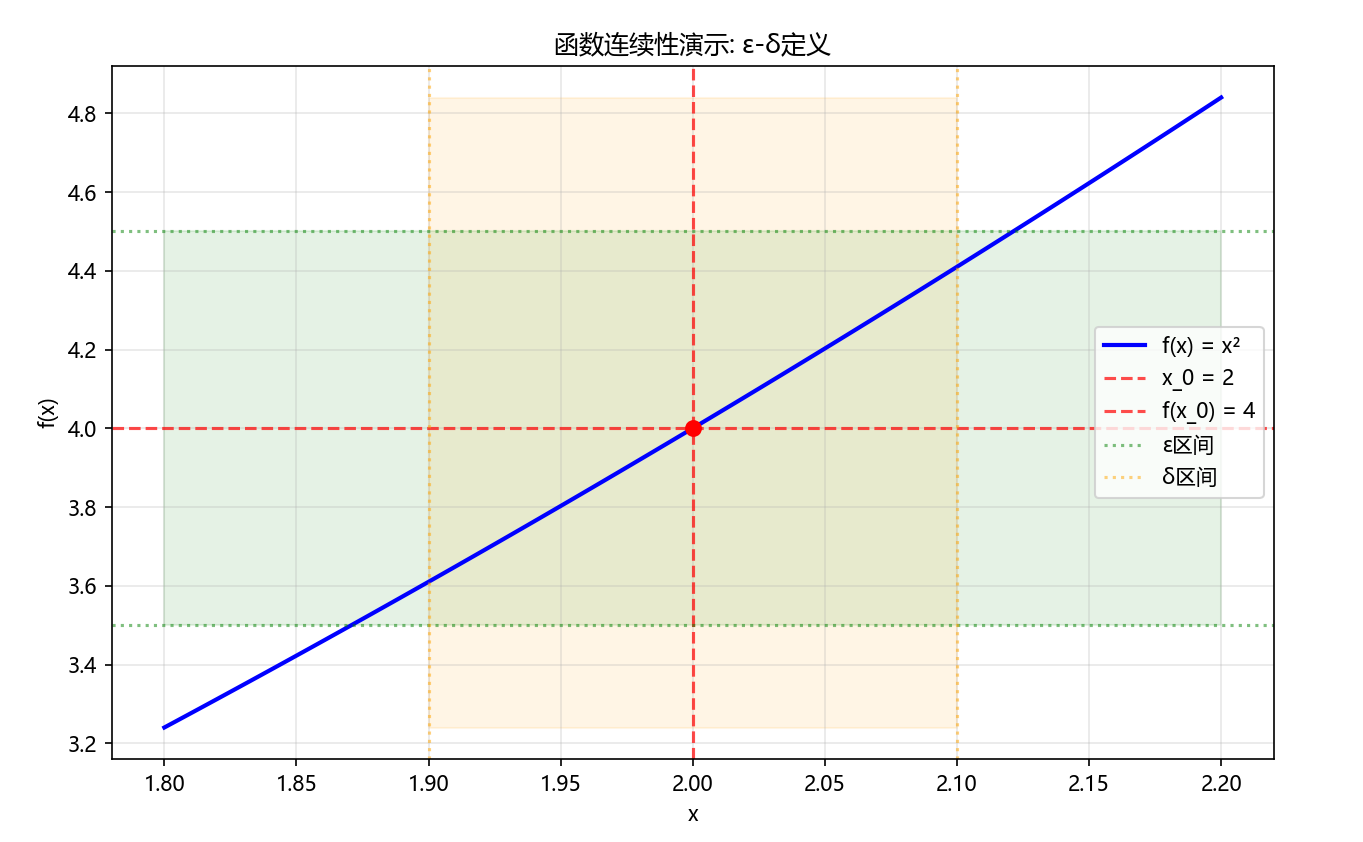
1.2 单侧连续性
数学定义:单侧连续性
- 左连续: lim x → x 0 − f ( x ) = f ( x 0 ) \lim \limits_{x \to x_0^-} f(x) = f(x_0) x→x0−limf(x)=f(x0)
- 右连续: lim x → x 0 + f ( x ) = f ( x 0 ) \lim \limits_{x \to x_0^+} f(x) = f(x_0) x→x0+limf(x)=f(x0)
定理:函数在一点连续的充要条件是在该点既左连续又右连续。
二、连续函数的局部性质
2.1 局部保号性:函数值的"传染性"
数学定理:如果函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处连续,且 f ( x 0 ) > 0 f(x_0) > 0 f(x0)>0,那么存在正数 δ \delta δ,使得当 x ∈ ( x 0 − δ , x 0 + δ ) x \in (x_0-\delta, x_0+\delta) x∈(x0−δ,x0+δ) 时, f ( x ) > 0 f(x) > 0 f(x)>0。
手动证明步骤:
- 由连续性定义,对 ε = f ( x 0 ) 2 > 0 \varepsilon = \frac{f(x_0)}{2} > 0 ε=2f(x0)>0,存在 δ > 0 \delta > 0 δ>0
- 当 ∣ x − x 0 ∣ < δ |x - x_0| < \delta ∣x−x0∣<δ 时, ∣ f ( x ) − f ( x 0 ) ∣ < f ( x 0 ) 2 |f(x) - f(x_0)| < \frac{f(x_0)}{2} ∣f(x)−f(x0)∣<2f(x0)
- 因此 f ( x ) > f ( x 0 ) − f ( x 0 ) 2 = f ( x 0 ) 2 > 0 f(x) > f(x_0) - \frac{f(x_0)}{2} = \frac{f(x_0)}{2} > 0 f(x)>f(x0)−2f(x0)=2f(x0)>0
- 证毕
Python代码:
import matplotlib.pyplot as plt
import numpy as np
# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei','DV Sans']
plt.rcParams['axes.unicode_minus'] = False
# 演示局部保号性
x = np.linspace(-2, 2, 1000)
f = lambda x: x**2 + 0.5 # 始终大于0的函数
x0, delta = 0.5, 0.8
plt.figure(figsize=(10, 6))
plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x² + 0.5')
# 标记邻域范围
plt.axvline(x=x0-delta, color='orange', linestyle=':', alpha=0.7)
plt.axvline(x=x0+delta, color='orange', linestyle=':', alpha=0.7)
plt.fill_between(x, 0, f(x), where=(x >= x0-delta) & (x <= x0+delta),
alpha=0.2, color='green', label='保号区间')
plt.title('局部保号性演示:f(x_o)>0 在x_o邻域内f(x)>0')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
Python代码执行结果: 在 x 0 = 0.5 x_0=0.5 x0=0.5 周围的邻域内,函数值始终大于0,直观演示局部保号性。
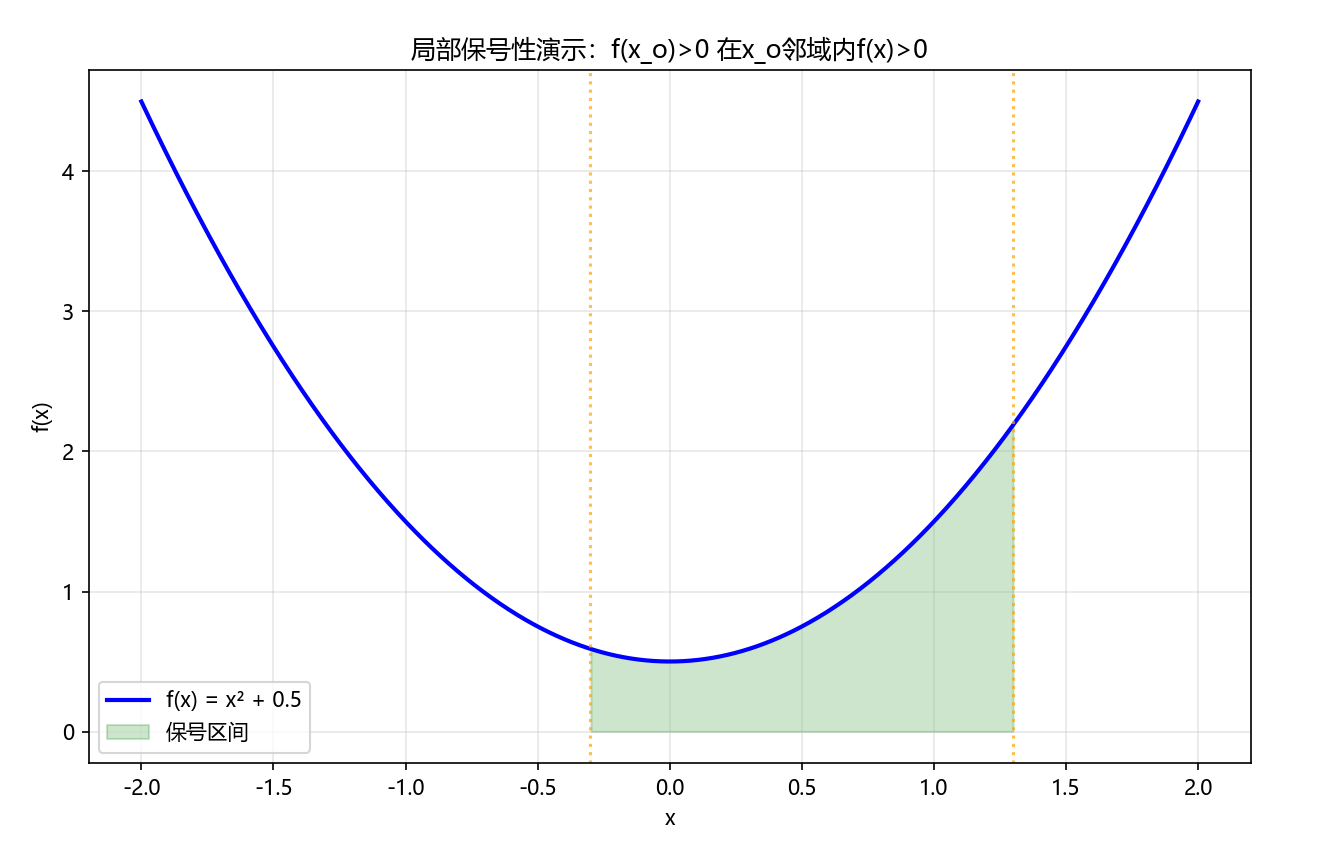
2.2 局部有界性:连续点的"稳定性"
数学定理:如果函数 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处连续,那么存在正数 δ \delta δ,使得 f ( x ) f(x) f(x) 在 ( x 0 − δ , x 0 + δ ) (x_0-\delta, x_0+\delta) (x0−δ,x0+δ) 上有界。
手动证明思路:
- 取 ε = 1 \varepsilon = 1 ε=1,由连续性,存在 δ > 0 \delta > 0 δ>0
- 当 ∣ x − x 0 ∣ < δ |x - x_0| < \delta ∣x−x0∣<δ 时, ∣ f ( x ) − f ( x 0 ) ∣ < 1 |f(x) - f(x_0)| < 1 ∣f(x)−f(x0)∣<1
- 因此 ∣ f ( x ) ∣ < ∣ f ( x 0 ) ∣ + 1 |f(x)| < |f(x_0)| + 1 ∣f(x)∣<∣f(x0)∣+1
- 函数在邻域内有上界 ∣ f ( x 0 ) ∣ + 1 |f(x_0)| + 1 ∣f(x0)∣+1 和下界 − ∣ f ( x 0 ) ∣ − 1 -|f(x_0)| - 1 −∣f(x0)∣−1
Python代码:
import matplotlib.pyplot as plt
import numpy as np
# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei','DV Sans']
plt.rcParams['axes.unicode_minus'] = False
def local_boundedness():
x0 = 1
delta = 0.5
x = np.linspace(x0 - delta, x0 + delta, 100)
f_x = np.sin(x) * np.exp(x) # 复杂但连续的函数
plt.figure(figsize=(10, 6))
plt.plot(x, f_x, 'b-', linewidth=2, label='f(x) = sin(x) * exp(x)')
plt.axvline(x=x0-delta, color='r', linestyle='--', alpha=0.7)
plt.axvline(x=x0+delta, color='r', linestyle='--', alpha=0.7)
# 计算上下界
upper_bound = max(f_x)
lower_bound = min(f_x)
plt.axhline(y=upper_bound, color='g', linestyle=':', label=f'上界: {upper_bound:.2f}')
plt.axhline(y=lower_bound, color='g', linestyle=':', label=f'下界: {lower_bound:.2f}')
plt.title('局部有界性演示')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
local_boundedness()
Python代码执行结果: 显示函数在 x 0 = 1 x_0=1 x0=1 邻域内的图像,并标出该区间内的上下界,验证局部有界性。
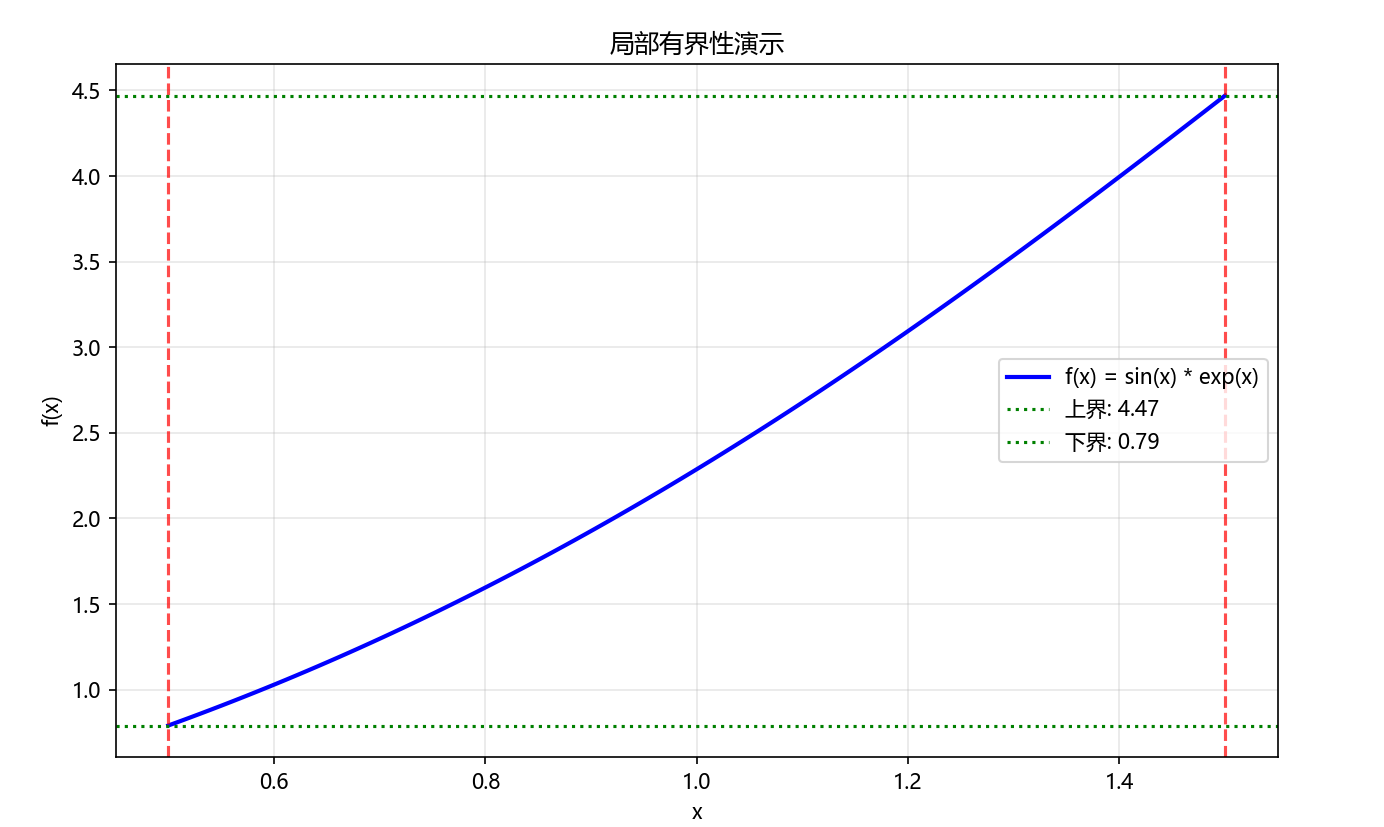
三、连续函数的全局性质
3.1 零点存在定理:方程的"解的存在保证"
数学定义:如果函数 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 上连续,且 f ( a ) f(a) f(a) 与 f ( b ) f(b) f(b) 异号,那么至少存在一点 ξ ∈ ( a , b ) \xi \in (a,b) ξ∈(a,b),使得 f ( ξ ) = 0 f(\xi) = 0 f(ξ)=0。
手动求解步骤:
- f ( x ) = 2 x + x f(x) = 2^x + x f(x)=2x+x 在 [ − 1 , 0 ] [-1,0] [−1,0] 上连续
- f ( − 1 ) = 2 − 1 − 1 = 0.5 − 1 = − 0.5 < 0 f(-1) = 2^{-1} - 1 = 0.5 - 1 = -0.5 < 0 f(−1)=2−1−1=0.5−1=−0.5<0
- f ( 0 ) = 2 0 + 0 = 1 > 0 f(0) = 2^0 + 0 = 1 > 0 f(0)=20+0=1>0
- 由零点存在定理,存在 ξ ∈ ( − 1 , 0 ) \xi \in (-1,0) ξ∈(−1,0) 使 f ( ξ ) = 0 f(\xi) = 0 f(ξ)=0
- 又因为 f ′ ( x ) = 2 x ln 2 + 1 > 0 f'(x) = 2^x \ln 2 + 1 > 0 f′(x)=2xln2+1>0,函数单调递增,零点唯一
Python代码:
import matplotlib.pyplot as plt
import numpy as np
# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
def prove_root_existence():
"""证明方程 2^x + x = 0 在(-1,0)内有唯一实根"""
x = np.linspace(-1, 0, 1000)
f = lambda x: 2**x + x
plt.figure(figsize=(10, 6))
plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = 2^x + x')
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
# 验证端点异号
f_minus1, f_0 = f(-1), f(0)
plt.scatter([-1, 0], [f_minus1, f_0], color='red', s=100)
plt.annotate(f'f(-1) = {f_minus1:.3f} < 0', (-1, f_minus1),
xytext=(-0.85, f_minus1 + 0.1))
plt.annotate(f'f(0) = {f_0:.3f} > 0', (0, f_0),
xytext=(-0.1, f_0 - 0.2))
# 寻找零点
root_x = x[np.argmin(np.abs(f(x)))]
plt.scatter([root_x], [f(root_x)], color='green', s=100,
label=f'零点 ξ ≈ {root_x:.3f}')
plt.title('零点存在定理:方程 2^x + x = 0 在 (-1,0) 内有根')
plt.xlabel('x');
plt.ylabel('f(x)')
plt.legend();
plt.grid(True, alpha=0.3)
plt.show()
prove_root_existence()
Python代码执行结果: 标注端点值和找到的零点位置,验证零点存在定理。
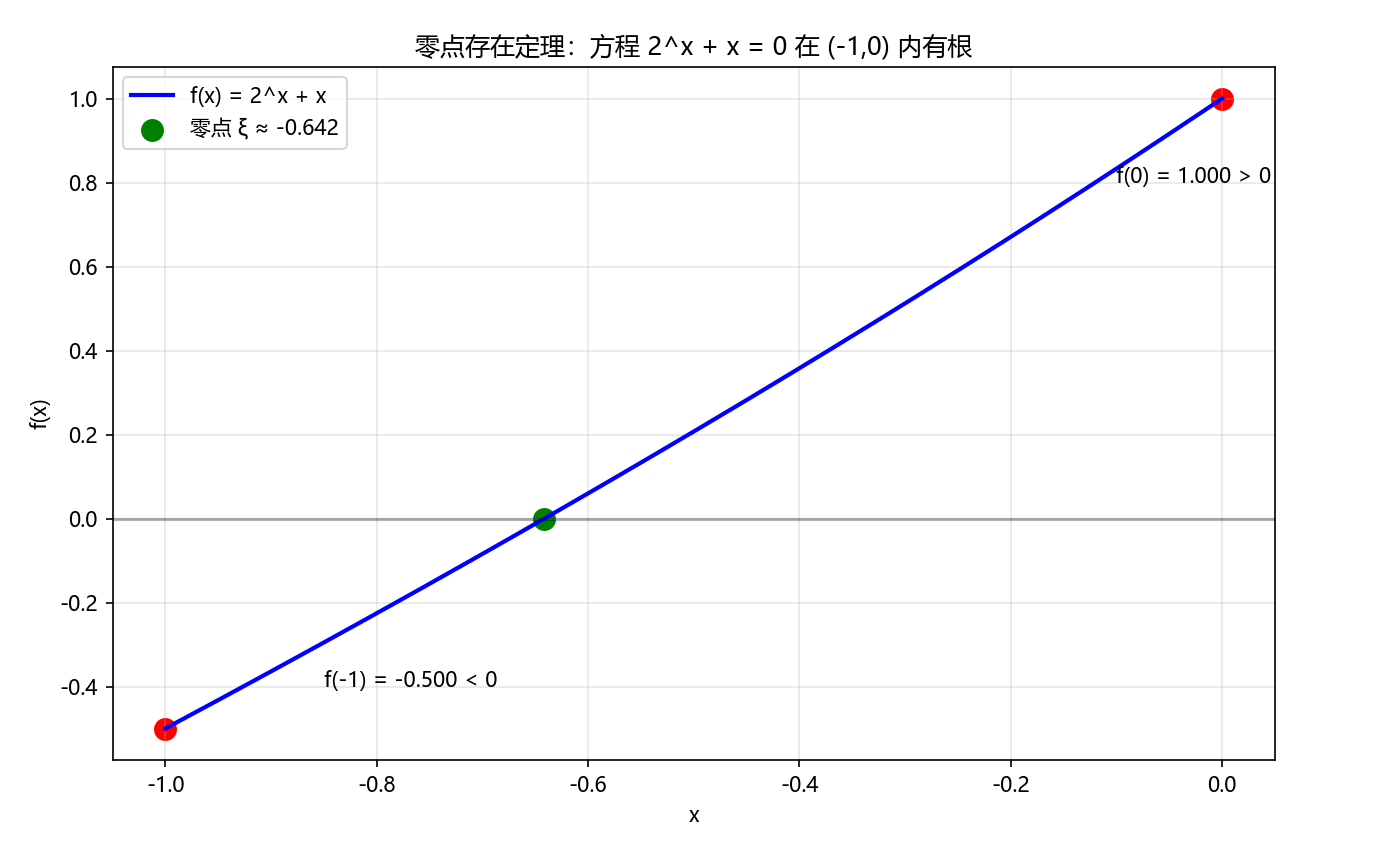
3.2 介值定理:函数值的"全覆盖性"
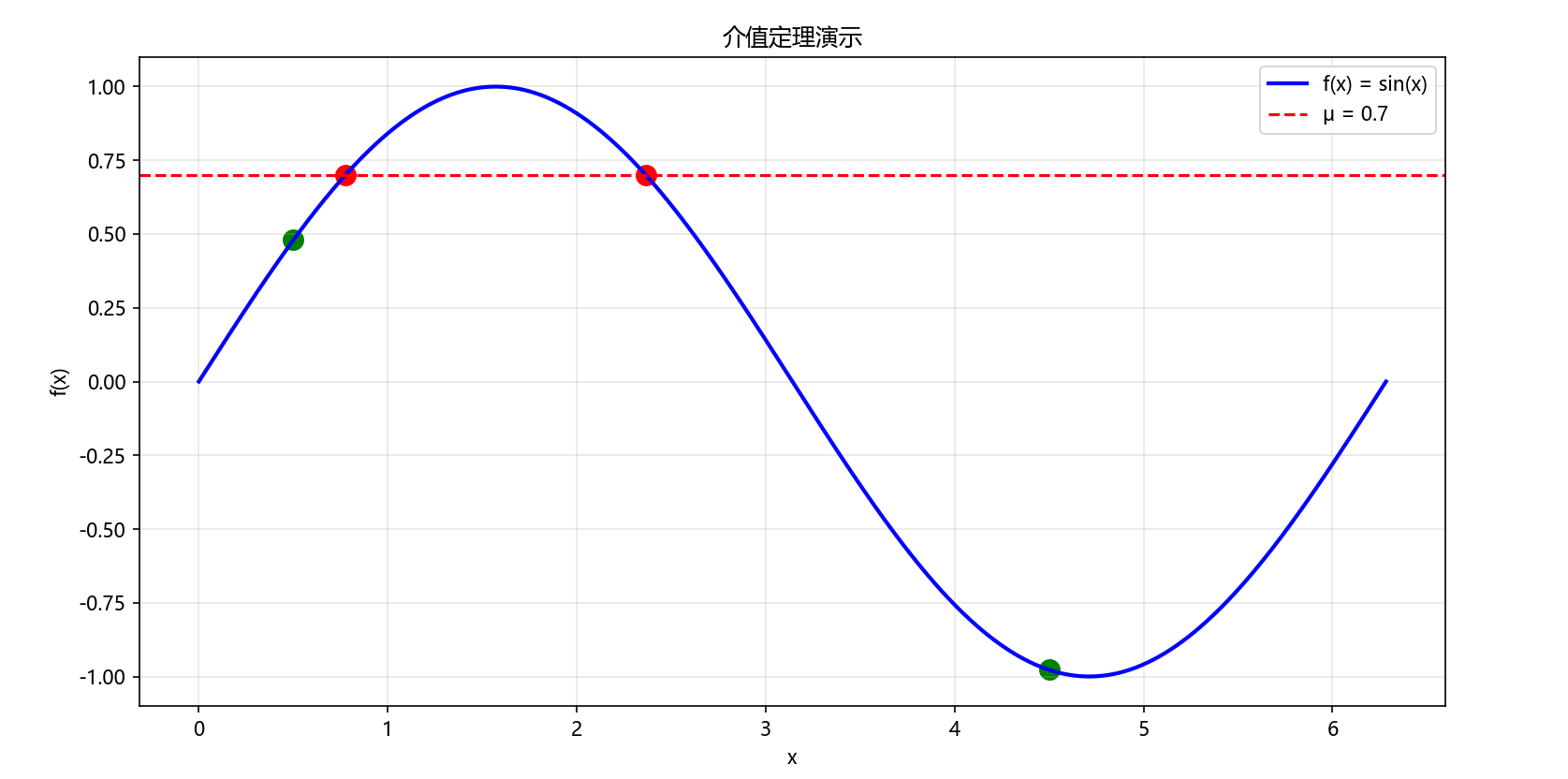
数学定义:如果函数 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 上连续,且 f ( a ) ≠ f ( b ) f(a) \neq f(b) f(a)=f(b),那么对于任意介于 f ( a ) f(a) f(a) 和 f ( b ) f(b) f(b) 之间的实数 μ \mu μ,至少存在一点 ξ ∈ ( a , b ) \xi \in (a,b) ξ∈(a,b),使得 f ( ξ ) = μ f(\xi) = \mu f(ξ)=μ。
手动证明思路:
- 构造辅助函数 g ( x ) = f ( x ) − μ g(x) = f(x) - \mu g(x)=f(x)−μ
- g ( a ) = f ( a ) − μ g(a) = f(a) - \mu g(a)=f(a)−μ 与 g ( b ) = f ( b ) − μ g(b) = f(b) - \mu g(b)=f(b)−μ 异号
- 由零点存在定理,存在 ξ ∈ ( a , b ) \xi \in (a,b) ξ∈(a,b) 使 g ( ξ ) = 0 g(\xi) = 0 g(ξ)=0
- 即 f ( ξ ) = μ f(\xi) = \mu f(ξ)=μ
Python代码:
def intermediate_value_theorem():
x = np.linspace(0, 2*np.pi, 1000)
f = np.sin(x)
a, b = 0.5, 4.5
mu = 0.7 # 介于sin(0.5)和sin(4.5)之间的值
plt.figure(figsize=(12, 6))
plt.plot(x, f, 'b-', linewidth=2, label='f(x) = sin(x)')
plt.axhline(y=mu, color='r', linestyle='--', label=f'μ = {mu}')
# 标记区间端点
plt.scatter([a, b], [np.sin(a), np.sin(b)], color='green', s=100)
# 寻找介值点
roots = []
for i in range(len(x)-1):
if (f[i] - mu) * (f[i+1] - mu) <= 0:
root_x = x[i] + (x[i+1] - x[i]) * (mu - f[i]) / (f[i+1] - f[i])
roots.append(root_x)
plt.scatter([root_x], [mu], color='red', s=100)
plt.title('介值定理演示')
plt.xlabel('x');
plt.ylabel('f(x)')
plt.legend();
plt.grid(True, alpha=0.3)
plt.show()
intermediate_value_theorem()
Python代码执行结果: 显示正弦函数图像,标注介值点,验证介值定理。
四、闭区间上连续函数的性质
4.1 有界性定理:闭区间上的"安全保证"
数学定义:如果函数 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 上连续,那么 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上有界。
定理证明概要:
- 利用有限覆盖定理:闭区间 [ a , b ] [a,b] [a,b] 的任意开覆盖都有有限子覆盖
- 由局部有界性,每点 x ∈ [ a , b ] x \in [a,b] x∈[a,b] 都有邻域 U ( x ) U(x) U(x) 使 f f f 在 U ( x ) U(x) U(x) 上有界
- U ( x ) x ∈ [ a , b ] {U(x)}_{x \in [a,b]} U(x)x∈[a,b] 是 [ a , b ] [a,b] [a,b] 的开覆盖,存在有限子覆盖
- f f f 在每个有限子覆盖区间上有界,因此在整个 [ a , b ] [a,b] [a,b] 上有界
Python代码:
def bounded_on_closed_interval():
x = np.linspace(0.1, 2, 1000)
f = lambda x: 1/x # 在(0,2]上连续,但在x=0无定义
plt.figure(figsize=(10, 6))
plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = 1/x')
# 在闭区间[0.5, 2]上验证有界性
a, b = 0.5, 2
x_closed = np.linspace(a, b, 100)
f_closed = f(x_closed)
upper_bound = max(f_closed)
lower_bound = min(f_closed)
plt.axvline(x=a, color='r', linestyle='--', label=f'区间[{a},{b}]')
plt.axvline(x=b, color='r', linestyle='--')
plt.axhline(y=upper_bound, color='g', linestyle=':', label=f'上界: {upper_bound:.2f}')
plt.axhline(y=lower_bound, color='g', linestyle=':', label=f'下界: {lower_bound:.2f}')
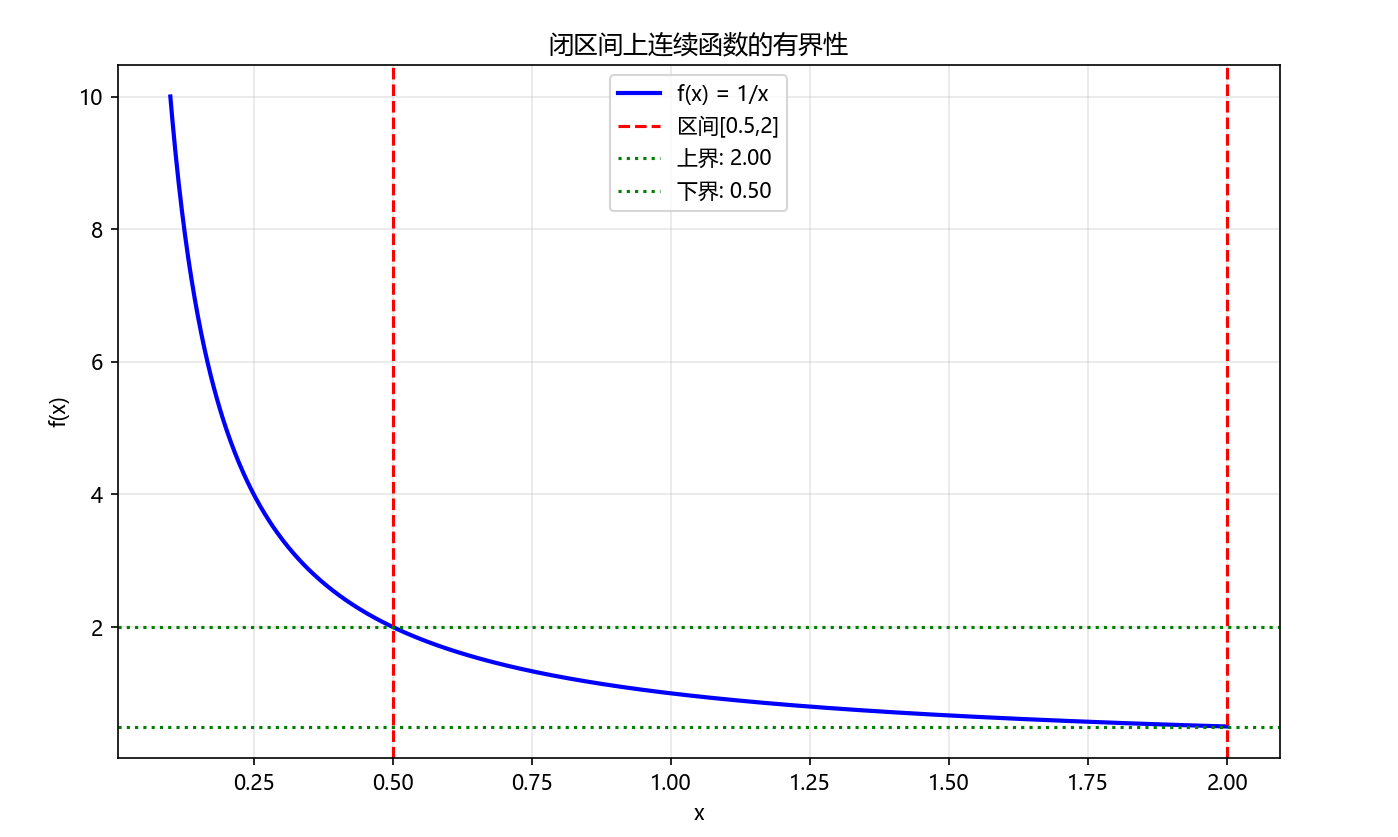
plt.title('闭区间上连续函数的有界性')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
bounded_on_closed_interval()
Python代码执行结果: 显示函数在闭区间上的图像,标注上下界,验证有界性定理。
4.2 最值存在定理:必然存在"冠军选手"
数学定义:如果函数 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 上连续,则存在 [ a , b ] [a,b] [a,b] 中的两点 ξ , η \xi, \eta ξ,η,使得对任意的 x ∈ [ a , b ] x \in [a,b] x∈[a,b],都有 f ( ξ ) ≤ f ( x ) ≤ f ( η ) f(\xi) \leq f(x) \leq f(\eta) f(ξ)≤f(x)≤f(η)。
证明思路:
- 由有界性定理, f ( [ a , b ] ) f([a,b]) f([a,b]) 是有界数集
- 令 M = sup f ( x ) : x ∈ [ a , b ] M = \sup{f(x) : x \in [a,b]} M=supf(x):x∈[a,b], m = inf f ( x ) : x ∈ [ a , b ] m = \inf{f(x) : x \in [a,b]} m=inff(x):x∈[a,b]
- 由上确界定义,存在数列 x n ⊂ [ a , b ] {x_n} \subset [a,b] xn⊂[a,b] 使 f ( x n ) → M f(x_n) \to M f(xn)→M
- 由闭区间紧性, x n {x_n} xn 有收敛子列 x n k → η ∈ [ a , b ] x_{n_k} \to \eta \in [a,b] xnk→η∈[a,b]
- 由连续性, f ( η ) = lim k → ∞ f ( x n k ) = M f(\eta) = \lim \limits_{k \to \infty} f(x_{n_k}) = M f(η)=k→∞limf(xnk)=M
- 同理可证最小值存在
Python代码:
def extreme_value_theorem():
x = np.linspace(-np.pi, np.pi, 1000)
f = lambda x: x*np.sin(3*x) + np.cos(x) # 复杂连续函数
plt.figure(figsize=(12, 6))
plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x·sin(3x) + cos(x)')
# 寻找最大值和最小值点
max_idx = np.argmax(f(x))
min_idx = np.argmin(f(x))
x_max, y_max = x[max_idx], f(x)[max_idx]
x_min, y_min = x[min_idx], f(x)[min_idx]
plt.scatter([x_max, x_min], [y_max, y_min],
color=['red', 'green'], s=100,
label=[f'最大值点 ({x_max:.2f}, {y_max:.2f})',
f'最小值点 ({x_min:.2f}, {y_min:.2f})'])
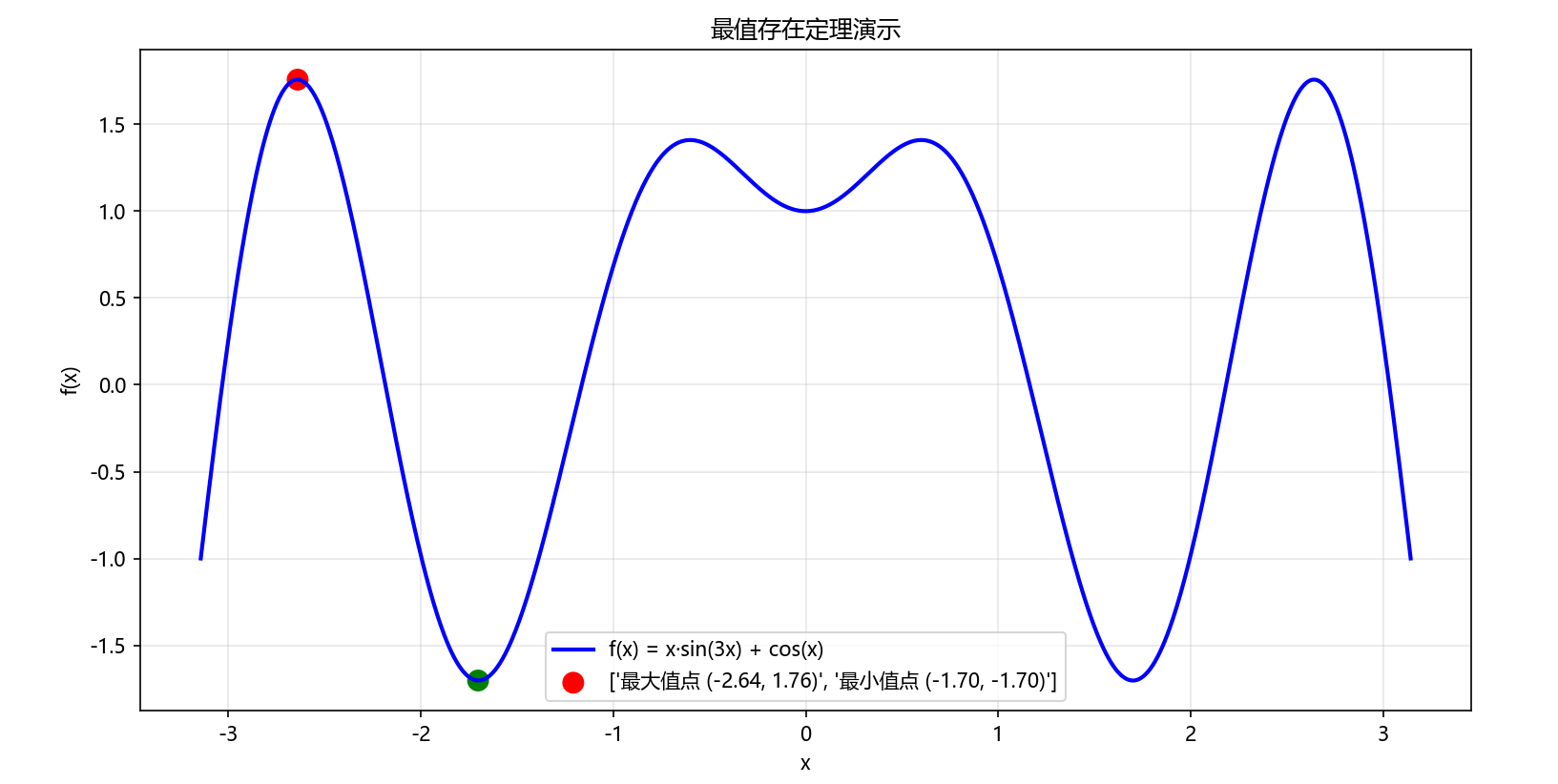
plt.title('最值存在定理演示')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
extreme_value_theorem()
Python代码执行结果: 显示函数图像,标注最大值点和最小值点,验证最值存在定理。
五、综合应用与Python实践
5.1 实例分析:物体运动问题
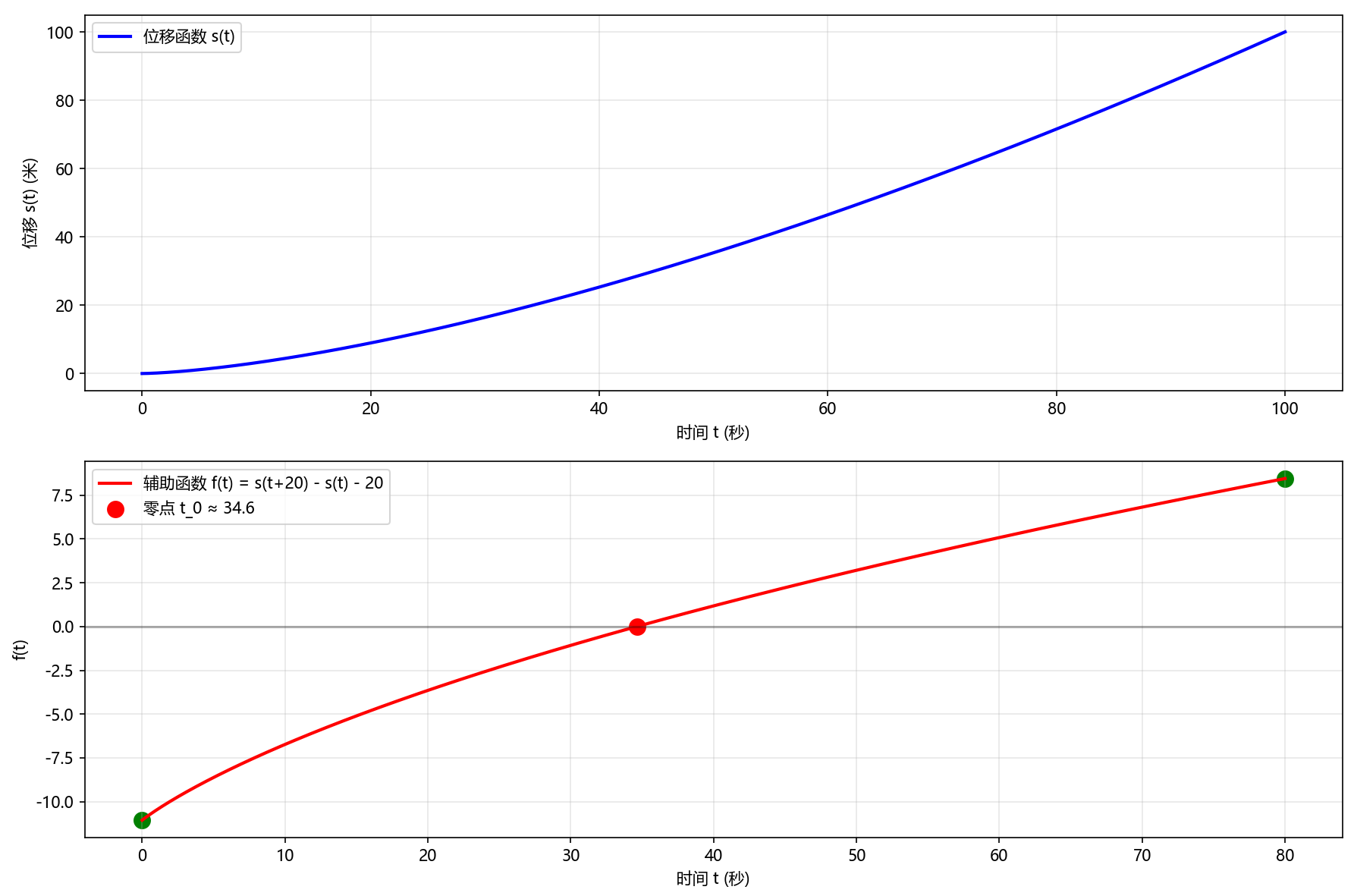
问题:设某物体用100秒钟连续移动了100米。求证存在某个时刻 t 0 t_0 t0,使得在时间段 [ t 0 , t 0 + 20 ] [t_0, t_0+20] [t0,t0+20] 中该物体恰好移动了20米。
手动证明:
- 定义位移函数 s ( t ) s(t) s(t),在 [ 0 , 100 ] [0,100] [0,100] 上连续
- 构造辅助函数 f ( t ) = s ( t + 20 ) − s ( t ) − 20 f(t) = s(t+20) - s(t) - 20 f(t)=s(t+20)−s(t)−20,在 [ 0 , 80 ] [0,80] [0,80] 上连续
- 计算端点值:
- f ( 0 ) = s ( 20 ) − s ( 0 ) − 20 f(0) = s(20) - s(0) - 20 f(0)=s(20)−s(0)−20
- f ( 80 ) = s ( 100 ) − s ( 80 ) − 20 f(80) = s(100) - s(80) - 20 f(80)=s(100)−s(80)−20
- 由题意, s ( 100 ) − s ( 0 ) = 100 s(100) - s(0) = 100 s(100)−s(0)=100,且运动连续
- 若 f ( 0 ) ⋅ f ( 80 ) ≤ 0 f(0) \cdot f(80) \leq 0 f(0)⋅f(80)≤0,由零点定理存在 t 0 ∈ [ 0 , 80 ] t_0 \in [0,80] t0∈[0,80] 使 f ( t 0 ) = 0 f(t_0) = 0 f(t0)=0
- 即 s ( t 0 + 20 ) − s ( t 0 ) = 20 s(t_0+20) - s(t_0) = 20 s(t0+20)−s(t0)=20
Python代码:
def motion_problem():
# 模拟物体运动函数
def s(t):
# 假设运动不是匀速的
return 100 * (t/100)**1.5 # s(0)=0, s(100)=100
t = np.linspace(0, 100, 1000)
positions = s(t)
# 定义辅助函数 f(t) = s(t+20) - s(t) - 20
t_inner = np.linspace(0, 80, 800) # t ∈ [0,80] 保证 t+20 ∈ [20,100]
f_t = s(t_inner + 20) - s(t_inner) - 20
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(t, positions, 'b-', linewidth=2, label='位移函数 s(t)')
plt.xlabel('时间 t (秒)'); plt.ylabel('位移 s(t) (米)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.subplot(2, 1, 2)
plt.plot(t_inner, f_t, 'r-', linewidth=2, label='辅助函数 f(t) = s(t+20) - s(t) - 20')
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
# 验证端点值
f0 = s(20) - s(0) - 20
f80 = s(100) - s(80) - 20
plt.scatter([0, 80], [f0, f80], color='green', s=100)
# 寻找零点
root_idx = np.argmin(np.abs(f_t))
t0 = t_inner[root_idx]
plt.scatter([t0], [f_t[root_idx]], color='red', s=100,
label=f'零点 t₀ ≈ {t0:.1f}')
plt.xlabel('时间 t (秒)'); plt.ylabel('f(t)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"f(0) = s(20) - s(0) - 20 = {f0:.2f}")
print(f"f(80) = s(100) - s(80) - 20 = {f80:.2f}")
print(f"存在 t₀ ≈ {t0:.1f} 使 f(t₀) = 0")
print(f"验证: s({t0:.1f}+20) - s({t0:.1f}) = {s(t0+20) - s(t0):.2f} 米")
motion_problem()
Python代码执行结果: 显示位移函数和辅助函数图像,找到满足条件的时刻 t 0 t_0 t0,并输出验证结果。

5.2 Python挑战练习
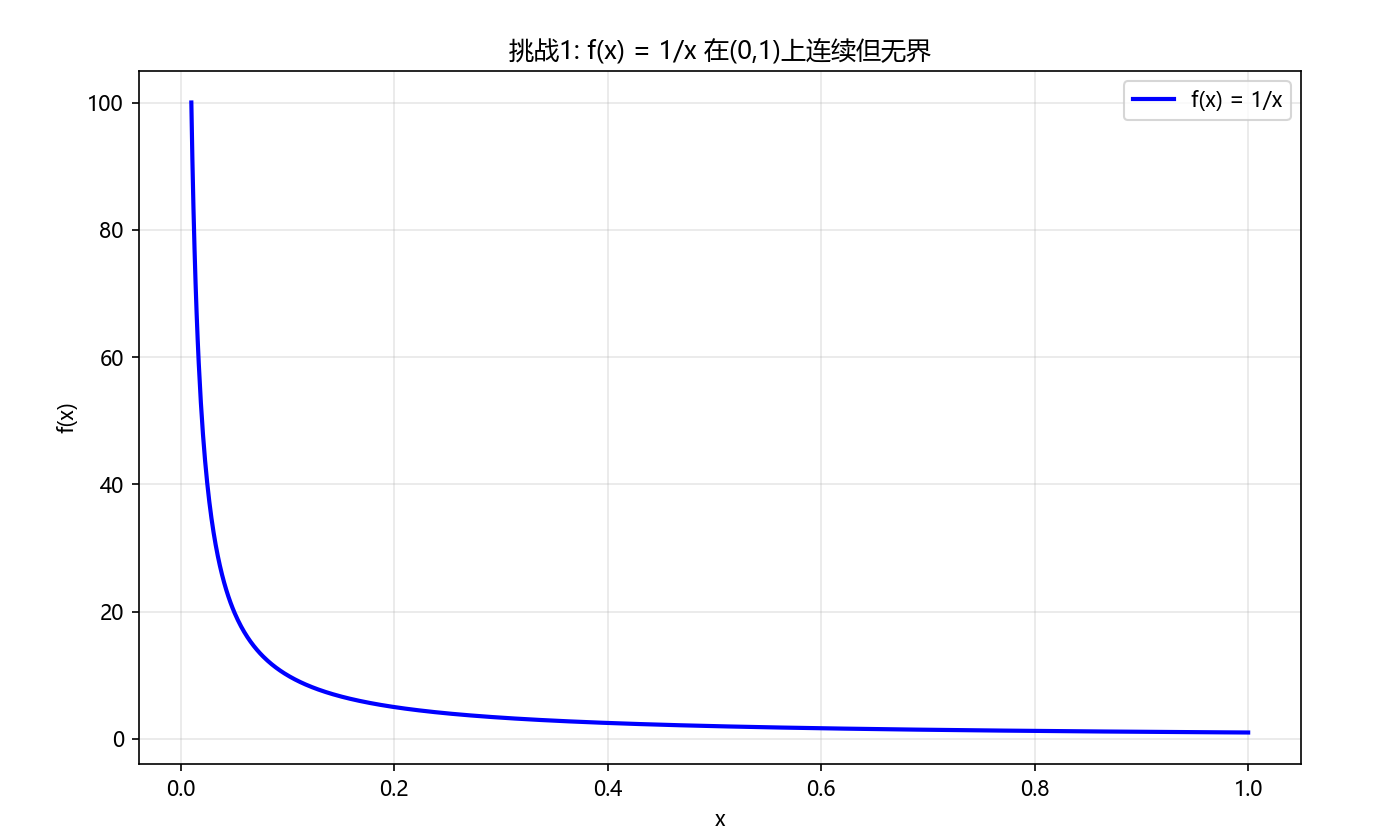
挑战1:验证函数 f(x) = 1/x 在(0,1)上连续但无界
手动分析:
- 在开区间(0,1)上,函数 f ( x ) = 1 / x f(x) = 1/x f(x)=1/x 是连续的
- 但当 x → 0 + x \to 0^+ x→0+ 时, f ( x ) → + ∞ f(x) \to +\infty f(x)→+∞,函数无上界
Python代码:
# 挑战1:验证函数 f(x) = 1/x 在(0,1)上连续但无界
def challenge1():
x = np.linspace(0.01, 1, 1000)
f = 1/x
plt.figure(figsize=(10, 6))
plt.plot(x, f, 'b-', linewidth=2, label='f(x) = 1/x')
plt.title('挑战1: f(x) = 1/x 在(0,1)上连续但无界')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
print("在开区间(0,1)上,当x→0⁺时,f(x)→+∞,函数无界")
challenge1()
Python代码执行结果:
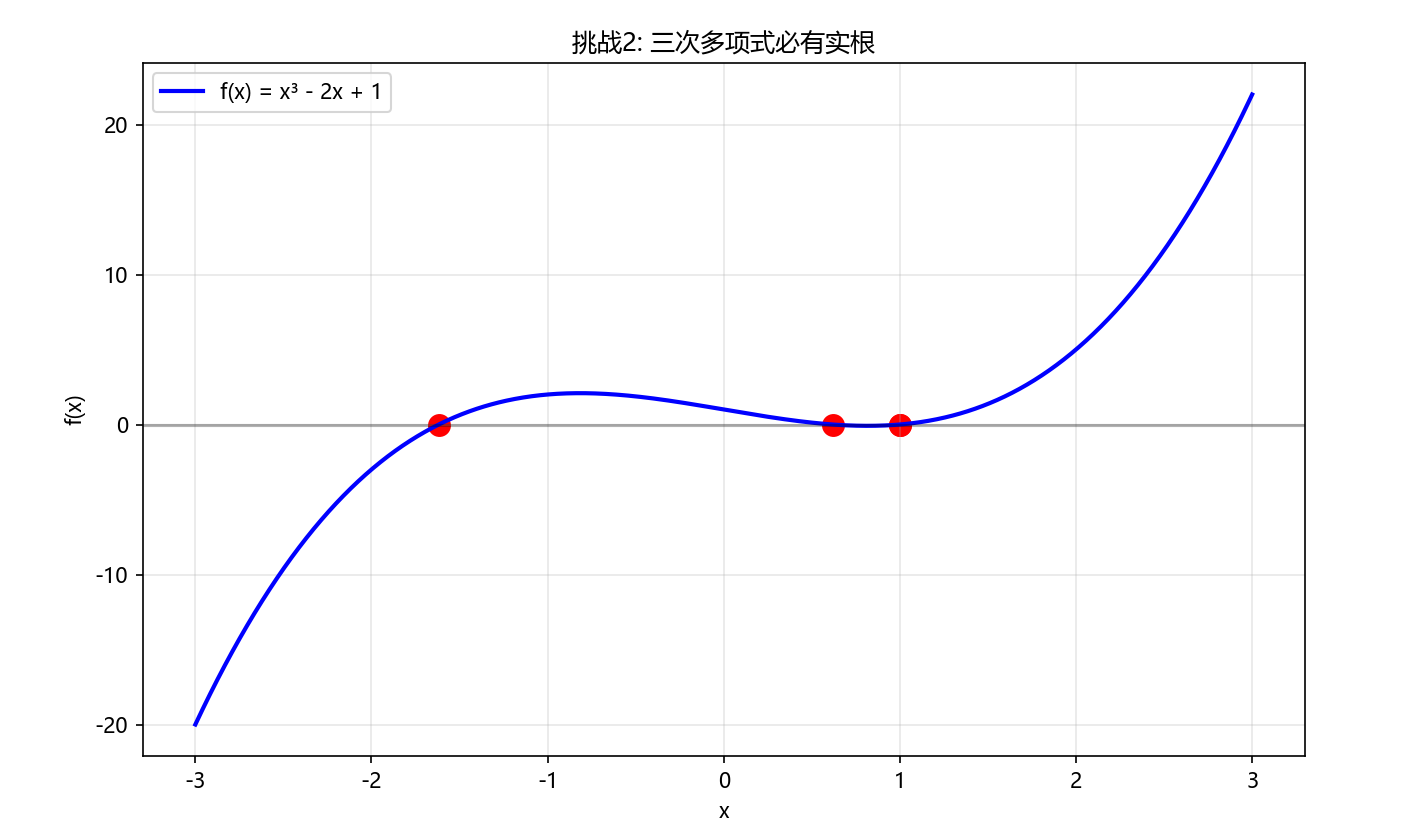
挑战2:绘制函数证明三次多项式必有实根
手动证明思路:
- 三次多项式 f ( x ) = a x 3 + b x 2 + c x + d f(x) = ax^3 + bx^2 + cx + d f(x)=ax3+bx2+cx+d( a ≠ 0 a \neq 0 a=0)
- 当 x → + ∞ x \to +\infty x→+∞ 时, f ( x ) → ± ∞ f(x) \to \pm\infty f(x)→±∞(取决于 a a a的符号)
- 当 x → − ∞ x \to -\infty x→−∞ 时, f ( x ) → ∓ ∞ f(x) \to \mp\infty f(x)→∓∞
- 由介值定理,必存在实根
Python代码:
# 挑战2:绘制函数证明三次多项式必有实根
def challenge2():
# 三次多项式至少有一个实根
x = np.linspace(-3, 3, 1000)
f = lambda x: x**3 - 2*x + 1 # 任意三次多项式
plt.figure(figsize=(10, 6))
plt.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x³ - 2x + 1')
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
# 验证存在实根
roots = []
for i in range(len(x)-1):
if f(x[i]) * f(x[i+1]) <= 0:
root = x[i] - f(x[i]) * (x[i+1] - x[i]) / (f(x[i+1]) - f(x[i]))
roots.append(root)
plt.scatter([root], [0], color='red', s=100)
plt.title('挑战2: 三次多项式必有实根')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
print(f"找到实根: {roots}")
challenge2()
Python代码执行结果:
六、总结与延伸学习
连续函数的性质为微积分奠定了坚实基础:
6.1 知识总结
- 局部性质:局部保号性、局部有界性,反映函数在一点附近的行为
- 全局性质:零点定理、介值定理,描述函数在整个区间上的特征
- 闭区间性质:有界性定理、最值定理,是优化理论的基础
6.2 学习建议
- 理论理解:结合几何直观理解每个定理的数学含义
- Python实践:通过可视化加深对抽象概念的认识
- 应用导向:将定理应用于实际问题求解
参考资料:扈志明,《微积分》,高等教育出版社
互动邀请:如果你有更好的可视化想法或发现了文章中的错误,欢迎在评论区留言讨论!






















 3526
3526












