Greedy Algorithm (1)——算法设计搬运

前言

终于进入算法部分了…

本来计划是照着 Victor 570 的内容来二次消化的，但是搬着搬着它就不香了——因为他跳过了太多非常有意思的内容。不看不知道，算法设计800多页的内容，Victor 自己删删减减硬憋出的教材来…就一言难尽…所以既然打算好好消化，那就正好啃一啃《Algorithm Design》这本书吧。

如果内容在 570 里也讲了，那么还是会引用到 570 课上的 Discussion Problem, 给出更多的示例——4.1, 4.4, 4.5。如果觉得比较有意思，想自己试试（实现一下），也会停下来去写码——比如 Victor 以比较复杂跳过的并查集实现之类的。总之补充章节难易不一，希望自己牙口好能啃得动，哒哒哒。

这次内容包含了第四章的前三节（除第一节之外都是没讲的）。

Chapter 4

贪心算法一般指在每一步都缺乏远见的选择眼下最优的条件去选择，一步步构建最终解的算法。——沃夏·朔德

核心是贪心策略的设计，以及能否证明贪心算法通过局部最优解的累积从而最终得到的解就是问题的全局最优解。

比如找零钱问题。给一定数额的钱，并给出各种面额的硬币，用最少数量的硬币找对方零钱。那么一种贪心策略就是尽可能优先使用面额最大的硬币去找。当然这种策略是不能保证得到最优解的。

所以一般贪心算法的难点就在于设计相应的贪心策略以及证明。

4.1 Interval Scheduling

Interval Scheduling: The Greedy Algorithm Stays ahead 这是标题全称。

是以区间调度和变形为例去解释，给出一类贪心策略最优解的证明

区间调度问题：有一集合包含$n$个 requests 的集合$S=1,2,...,n$，并且请求 $i$ 会有请求开始时间 $s_i$ 和结束时间 $f_i$. 让你设计一个算法给出调度安排，使得我们在一段时间 $T$ 内能够处理尽可能多的请求。

实用场景可以想象成场地租赁等。使用需提前打好请求，什么时间段用，负责人进行相应安排…

Algorithm Design

In short(书上一堆引导思考的话就不搬了)，一般会想到 (a) 优先安排开始时间早的——然后发现不保证最优，因为时间占用时间很长；到 (b) 优先安排使用时间短的——也不能保证，因为可能短的会与其他申请冲突，造成更大资源的浪费，再到 ( c )，先安排冲突最少的，发现也不可以。见下图：

能够保证最优的是按结束时间，选择最小的可容请求$f_i$。背后的想法是我们尽可能地让我们请求尽可能早结束，资源占用也就越空闲。

Proof

下面证明其optimality。

首先证明，贪心算法解 $I$ 与最优解 $O$ 相比，我们的请求调度确保“领先”。对于两种调度的安排选择的第$j$项，$f(I_j)\le f(O_j)$.

然后通过这个性质，再证明$|I|=|O|$, 二者处理请求数相同。

第一点的归纳证明。
Base Case. 显然 $f(I_1)\le f(O_1)$，我们选择的就是第一个结束的请求。
Induction Hypothesis. 前 $i-1$ 项，满足$f(I_{i-1})\le f(O_{i-1})$.
Induction Step. 证明对于第 $i$ 项，IH 依然成立。
首先 $f(O_{i-1})\le s(O_i)$, 再结合 IH, $f(I_{i-1})\le f(O_{i-1})\le s(O_i)$. 即对于贪心算法而言，第 $i$ 项请求总可以选择最优解的第 $i$ 项。
而算法所选的是可兼容的请求中结束时间最早的，所以 $f(I_i)\le f(O_i)$——贪心算法保持领先。

第二点用反证法。
假设 $k=|I|<|O|=m$.
那么由“贪心算法保持领先”可知，$f(I_i)\le f(O_i)$, 当 $i\le k$. 又因为$f(O_k)\le s(O_{k+1})$, 所以$f(I_k)\le f(O_k)\le s(O_{k+1})$. 贪心算法也可以接着安排 $O_{k+1}$，而不会停止。
得出矛盾，所以$k=|I|=|O|=m$.

Complexity

复杂度$O(n\log n)$, 全在排序上。排完序扫一遍就够了。

Extensions

• 当我们不能事先知道所有申请时，而是必须要实时做出决策处理或者拒绝请求，则就变成了相应在线算法的研究(online algorithm)，不知道future input的情况下决策(请求可能因的等待时间过长而expired)——以后大概率不会搬。

• 另一个问题是优化目标从出力最多请求，而变成可以获得的报酬(回馈，reward)最大化。处理请求会消耗相应一定的资源，但也会有相应的 reward。找到最大化利润的资源分配方式，变成了 DP 问题——到时候会搬。（挖个坑，#微笑）

Related Problems

基站问题

一个类似的问题是建基站问题。要给一条线上的所有村庄覆盖信号。而基站的覆盖范围是4km，求建立基站最少的方案。

思路：先走到一个没被信号覆盖的村庄，然后走4km放一个基站。接着往前走，重复上过程。

证明思路是几乎完全相反，证明的是贪心算法“stays behind”。归纳证明，$L(I_j)\ge L(O_j)$. 然后反证法证明$|I|\le |O|$.

作业里面也有一道几乎完全一样的停车加油问题。一维距离，加油站位置$d_1<d_2<...<d_n$，在加油站停可以加满油。车在满油箱时可以跑 $p$ miles，且相邻两加油站之间距离不超过 $p$, 求到达终点且在加油站停下次数最少的方案。也是一个道理。

Interval Partitioning

扩展: Interval Partitioning. 依然假定请求都有开始和终止时间，但我们有多个资源池可以处理请求。求处理一批请求所需的最少资源方案。如图：

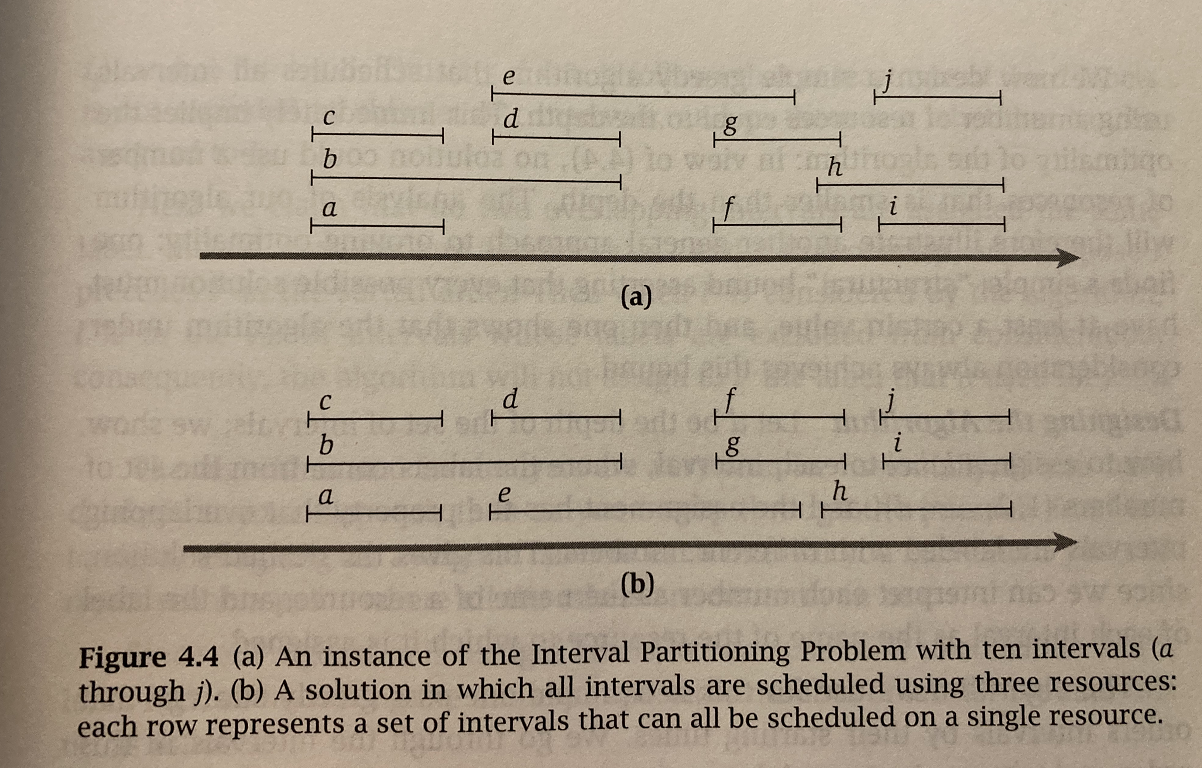
那么这里利用一个性质：某一时刻的请求最大冲突数（区间集合的深度，某一时刻overlapping的请求数）就是最少需要的资源数。这个很好理解就不给证明了。

算法思路：先排序，然后按照depth从 1:d，对于当前请求 $r_i$，对于它的备选 label 集合中去除掉所有在它之前并且 overlap 的请求的 label（整个循环结束如果某个请求的标签有多个备选则随便选一个）。

复杂度: $O(n\cdot d+n\cdot \log n)$

4.2 Scheduling to Minimize Lateness

全称：Scheduling to Minimize Lateness: An Exchange Argument

这部分内容 TU Delft 的 slides 讲得也很明白，可以康康。

Algorithm Design

问题: 在一个区间的时间 $s$ 可以使用资源，来处理请求。与之前不同之处在于此时我们的请求不在固定开始和结束时间，而是更加灵活——请求 $i$ 有一个 deadline $d_i$，处理该请求需要持续分配资源，耗时 $t_i$. 随时可以安排处理该请求，也允许请求的响应处理不及时。

但是优化的目标也变得复杂——对于所有请求选择适当的开始时间 $s(i)$ 就会得到相应的请求处理结束时间 $f(i)$. 我们的目标是$$MIN(MAX(L_i))$$，最小化最高延迟。

（图片来自 TU Delft 的 slides）

书中引导启发的文字叙述部分 in short——(a) 优先安排 $t$ 短的，显然不能最优，$t_1=1,t_2=9,d_1=20,d_2=9$，此时先安排 $r_1$ 就不是最优了；(b) 按照最晚开始时间 $d_i-t_i$ 来排序安排，这样也不行。比如 $t_1=1,d_1=2,t_2=10,d_2=10$, 此时先安排$r_2$ lateness $L=9$, 而先安排 $r_1$, $L=1$.

直接上答案——Earliest Deadline First——其实如最朴素的的 Interval Scheduling 类似一样直接按照 $d_i$ 的递增顺序安排就可以保证最优，这个证明比较有意思。

Proof

如何来来证明 Earliest Deadline First 的 optimality 呢？

这里的思路是 Exchange Argument. 我们从最优解 $O$ 开始入手，在保留其最优性的前提下，一步步地调整最优解，最终将其转化成与我们使用的贪心算法——Earliest Deadline First 所找到的解一样(identical)的解。

在一步步转化的过程中，就会涉及到一些贪心算法的性质，有针对的引入一些定理。

(4.7) There is an optimal schedule with no idle time.

这点比较清晰，因为缩短两个任务之间的空闲时间不会增加延迟，所以一定存在请求处理之间没有空闲时间的最优解（schedule）。

然后是引入一个概念 inversion, 转置。

对于请求 $r_i$ 和 $r_j$, 如果 $d_i<d_j$, 但 $r_j$ 却被安排在 $r_i$ 之前，那么便存在一个 inversion.

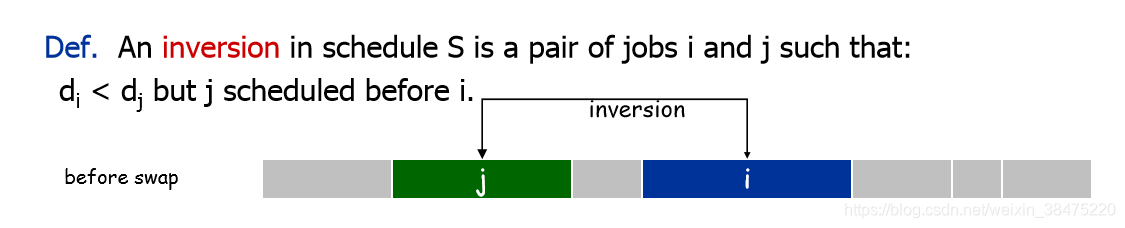
(4.8) All schedules with no inversions and no idle time have the same maximum lateness.

Proof. 证明起来比较简单，即便两个不同的计划都没有转置和空闲时间，也不一定就有相同的请求处理顺序。
但是对于 deadline 不同的请求，他们的安排是一样的；唯一的不同在于 deadline 相同的多个请求处理顺序可能不同。但是对于后者，deadline 相同的请求，在某一时间点连续安排的顺序并不影响它们中的最大延迟。所以整体的最大延迟也是相同。

接下来通过一系列性质来证明“一定存在一个没有空闲时间和转置的最优解 $O^{{}^{\prime }}$。

(4.9) There is an optimal scedule that has no inversions and no idle time.

(a) If $O$ has an inversion, then there is a pair of jobs $i$ and $j$ such that $j$ is scheduled immediately after $i$ and has $d_j<d_i$.

Proof. 这点也比较好理解。如果不存在转置的话，那么按照处理的顺序，所有请求 deadline 一定是非递减的，要么增要么相同。如果存在转置，就一定会在某一次请求处理之后出现了 deadline 减小，而此时转置必然发生于两相邻请求间。

(b) After swapping $i$ and $j$ we get a schedule with one less inversion.

这个只要是一对儿转置，无论怎么交换转置的数量都会减一。但是我们在这里对于最优解 $O$，从前往后的处理所有请求，当 deadline 减小，即出现相邻请求转置时，交换两请求处理顺序。最多 $C_n^2$ 个转置，每次交换减少一个转置。

(c.) The new swapped schedule has a maximum lateness no larger than that of $O$.

我们在上一步交换了两个相邻的，形成转置的请求。在这里证明，我们的延迟并未增加。

对于交换之前，$L(i)=f_i-d_i,L(j)=f_j-d_j$.
交换之后，$L^{{}^{\prime }}(i)=f_i^{{}^{\prime }}-d_i,L^{{}^{\prime }}(j)=f_j^{{}^{\prime }}-d_j$.

显然 $f_i>f_i^{{}^{\prime }}$, 所以$f_i-d_i=L(i)>L^{{}^{\prime }}(i)=f_i^{{}^{\prime }}-d_i$. 则对于请求 $i$, 它的延迟变低了。

比较棘手的是对于请求 $j$ 的分析。
因为 $f_i=f_j^{{}^{\prime }},d_i<d_j$, 所以 $L(i)>L^{{}^{\prime }}(j)$. 也就是交换之后，无论请求 $j$ 的延迟变得如何差，它都是有界的。它的延迟一定比交换之前请求 $i$ 的延迟小。

所以交换之后，依然是 optimal.
则重复这个过程，任意最优解就被转换成就是没有空闲时间，且按 deadline 非递减顺序处理的最优解——与贪心算法解一致（$L$是最优解延迟）。

(4.10) The schedule produced by the greedy algorithm has an optimal lateness L.

Complexity

按 deadline 排序, 再扫一遍。$O(n\log n)$.

Extensions

我们的问题存在一个假设——所有请求都可以从开始时刻 $s$ 处理。而我们对于 Earliest Deadline First 的最优性分析非常依赖于此。

这个问题的一种扩展是每个请求 $i$ 除了带有 $t_i$ 和 $d_i$, 都有最早可以开始的时间 $s_i$，即 release time. 比如跟口腔科打电话“某天8点到11点半之间可以预约么”…

吼吼，此时问题就变成了NP，到第8章见分晓！(再挖个坑…)

4.3 Optimal Caching

全称：Optimal Caching: A More Complex Exchange Argument

这一节的目的是证明该算法的最优性，以其为代表讲更复杂的Exchange Argument.

Algorithm

问题. 回顾操作系统的知识：1、三级存储结构，外存，内存，cache；2、Belady’s Algorithm，当cache miss 且满了，根据访问序列交换未来最远用到的块出内存，再换进要访问的块。也被称为 Farthest-in-Future Algorithm.

假设 cache 块大小 $k=3$, 初始内容 {$a,b,c$}. 按照Belady’s Algorithm 维护。访问序列$$a,b,c,d,a,d,e,a,d,b,c$$, 则step 4 cache miss 换出 $c$, step 7 cache miss 换出 $b$.

优化目标是最少的 cache miss.

(4.11) $\overline{S}$ is a reduced schedule that brings in at most as many items as the schedule $S$.

所谓 reduced schedule 指的是仅在迫不得已情况下（cache miss 且满了）才交换。

这个定理说的是对于任何 nonreduced schedule, 都会存在一个"equally good"的 reduced schedule.

假设 $S$ 是一个调度计划，在step $i$ 没有申请块 $d$ 的情况下，却访问了 $d$ 把它调进了 cache. 那么对于 $\overline{S}$, 既然我们在这个时候压根就不会用到 $d$, 索性我们就在这一步什么都不干假装调进来了。然后在后面需要用到 $d$时（step $j$），再从内存里面访问 $d$ 把他换到 cache 里。

reduced schedule 换入的次数就是 cache miss的数量。‘’

Proof

通过 Exchange Argument 证明 Farthest-in-Future Algorithm 的 optimality.

对于任意的内存访问序列 $D$，$S_{FF}$ 表示 贪心算法 Farthest-in-Future Algorithm* 得到的调度，$S^{\ast }$ 表示最优调度。我们在不增加 cache miss 的前提下，将后者的换出决定(eviction decision)一步步转化成前者。

(4.12) Let $S$ be a reduced schedule that makes the same eviction decision decisions as $S_{FF}$ through the first $j$ items in the sequence $D$, for a number $j$. Then there is a reduced schedule $S^{{}^{\prime }}$ that makes the same eviction as $S_{FF}$ through the first $j+1$ items, and incurs no more misses than $S$ does.

对于第 $j+1$ 次 request，item $d=d_{i+1}$. 因为 $S$ 和 $S_{FF}$ 的前 $j$ 次决策一致，所以它们的 cache contents 相同。

• case a: 如果 $d$ 此时已在 cache 中，cache hit 则因为二者都是 reduced schedule, 则可以令 $S^{{}^{\prime }}=S$，二者前 $j+1$ 次换出决策一致，剩下的也可以构造一致，所以 miss 数可以相同.

• case b: 此时 $d$ 不在 cache 里，且 cache 不满，那就直接 load $d$ 进 cache，不需要考虑换出，同样的 $S^{{}^{\prime }}=S$, miss 数相同.

• case c: 此时 $d$ 不在 cache 里，且 cache 满了，需要考虑换出哪一块。不妨设 $S$ 换出 $f$, 而 $S_{FF}$ 换出 $e,e\ne f$. (如果 $e=f$ 则天然的 $S^{{}^{\prime }}=S$)

因为我们对于 $S^{{}^{\prime }}$ 的构造要保持两点:

• ($i$) $S^{{}^{\prime }}$ 和 $S_{FF}$ 的前 $j+1$ 项决策相同
• ($ii$) $S^{{}^{\prime }}$ 的 cache miss 数不超过 $S$.

所以此时对于 case c 中 $S^{{}^{\prime }}$ 的构造，我们就必须要在 就 $j+1$ 步 换出 $e$, 保证前 $j+1$ 步都与 $S_{FF}$ 一致。然后接着构造 $S^{{}^{\prime }}$ 使它的 miss 数不超过 $S$. 这点最简单的办法就是想办法让 $S^{{}^{\prime }}$ 和 $S$ 在剩余的 sequence 上都决策一致。

但是问题在于经过第 $j+1$ 步，二者的 cache content 不同了。$S^{{}^{\prime }}$ 中留得是 $f$, 而 $S$ 中留的是 $e$. 那么就想办法让他们俩尽快保持 content 相同，剩下的就可以构造一致从而保证 miss 数不超过 $S$.

那么开始。从第 $j+2$ 次请求开始，令 $S^{{}^{\prime }}$ 的决策与 $S$ 相同，直至出现下面任一种情况：

• ($i$). 此时请求块 $g,g\ne e$, 且 cache miss. 并且 $S$ 此时换出 $e$. 因为当前 $S^{{}^{\prime }}$ 和 $S$ 唯一的不同就在于一个 cache 里面存的是 $e$，另一个是 $f$. 那么现在 $S$ 要把 $e$ 换出去，把 $g$ 换进来。相应的 $S^{{}^{\prime }}$ 换出 $f$，换入 $g$. 余下的 sequence 决策全部与 $S$ 相同即可。cache miss 数相同。

• ($ii$). 此时请求 $f$，且 $S$ 换出块 $e^{{}^{\prime }}$. 此时两种情况：

  • $e^{{}^{\prime }}=e$. 那么 $S^{{}^{\prime }}$ 的 cache 已经存了 $f$，do nothing, 余下的 sequence decision 同 $S$ 一致即可。
  • $e^{{}^{\prime }}\ne e$. 那么 $S^{{}^{\prime }}$ 同样的换出 $e^{{}^{\prime }}$, 把 $e$ 换进来就与 $S$ 的 cache content 一致。余下的也保持一致即可。注意此时 $S^{{}^{\prime }}$ 不是一个 reduced schedule——在 request $f$ hit 时却把块 $e$ load 进来，但根据 (4.11) 我们可以把 $S^{{}^{\prime }}$ 转换成 $\overline{S^{{}^{\prime }}}$, 不会增加 cache miss 数. 然后令 $S^{{}^{\prime }}=\overline{S^{{}^{\prime }}}$ 就完成了。

无论如何我们总会在 request $e$ 之前遇到这两种情况中之一。因为根据 Farthest-in-Future Algorithm 的性质，在 $j+1$步，$e$ 而不是 $f$, 之所以在 $S_{FF}$ 某一步被换出，是因为 $e$ 在未来的引用要比 $f$ 的引用晚。

(4.13) $S_{FF}$ incurs no more misses than any other schedule $S^{\ast }$ and hence is optimal.

因此对于 $S^{\ast }$, 利用 (4.12) 一步步构造，从 第一个决策开始 $S_1$ 跟 $S_{FF}$ 第一项一致，得到 miss 数不超 $S^{\ast }$ 的 $S_2$… 重复这过程直到 $j=n$. 则对整个 sequence, $S_n=S_{FF}$.

Extensions

其实本科操作系统最后还是说了 Belady’s Dilemma. 因为没法预知未来…

所以 LRU 成为了以回顾过去试图去窥探未来的比较好的方法。同时也契合程序的局部性原理 (locality of reference).

在 LRU 应用很久之后，Sleator 和 Tarjan 给出了 LRU 性能的理论分析——bounding the number of misses relative to Farthest-in-Future. 这部分内容分析以及LRU 的 randomized variant 会在第13章随机算法的 caching problem 里面讲。（深渊巨坑…）