有趣的高数、线代、概率教材,我推荐马同学图解系列。感兴趣的话可以通过“阅读原文”购买。

1 看懂
数学的定义看上去让人望而却步,比如:
设函数 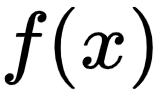 在
在  上有定义。
上有定义。
如果存在常数 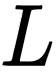 ,对任意给定的正数
,对任意给定的正数 (不论它多么小),总存在正数
(不论它多么小),总存在正数  ,使得当
,使得当  满足不等式
满足不等式  时,对应的函数值
时,对应的函数值 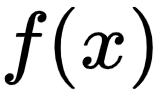 都满足不等式:
都满足不等式:

那么常数 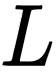 就叫做函数
就叫做函数 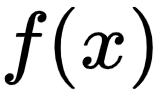 当
当  的极限,记作:
的极限,记作:

一般函数的极限定义
上面那段是微积分里的最基本概念,极限。是不是有一种,每个字都认识,但不知道在讲什么的感觉?图解课程希望用图让你看懂。
1.1 动图
首先来个运动过程把握下整体:

1.2 静态图
再用分帧讲解,展现细节:

1.3 互动图
光看还不行,那就动下手吧:

1.4 练习
光说不练假把式,检验懂不懂的最好方法,当然是做题:

2 持续看懂
数学语言不是生活语言,往往看到后面时,前面的内容已经有所遗忘,这样还是会导致看不懂。
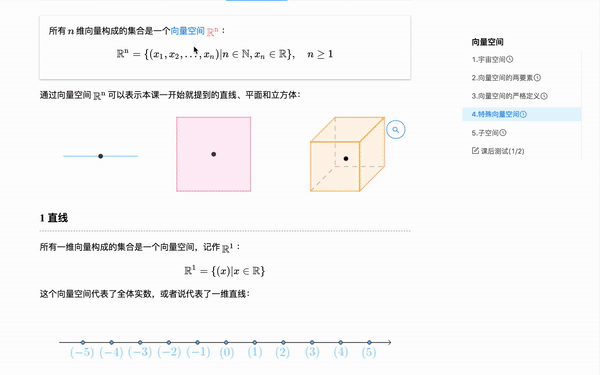
2.1 知识点引用
为此,作为线上教材,我们有知识点引用:
2.2 关键字搜索
如果引用的关键字仍不能使同学解惑,教材还配有关键字搜索:

2.3 知识的关联
更重要的是,数学知识并不割裂,它应该有一条清晰的逻辑链。因此,马同学的教材也注意前后知识点的联结:
在单变量微积分中介绍过,可以用 切线 来近似(“代替”)  点附近的曲线,这就是一种以直代曲,这样的近似会大大降低处理曲线问题的难度:
点附近的曲线,这就是一种以直代曲,这样的近似会大大降低处理曲线问题的难度:

同样的,在多变量函数中,我们需要找到一个平面来近似  附近的曲面:
附近的曲面:

摘自马同学多变量微积分
3 细节
数学不容易看懂,或者以为看懂其实没看懂,还有一个原因是细节太多了。图解课程力争展现更多的细节。
3.1 没被发现的细节
切线函数和微分函数的区别在于,前者在  坐标系下,后者在
坐标系下,后者在 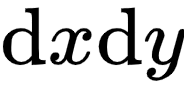 坐标系下:
坐标系下:

因此,两者的自变量和因变量是有区别的:
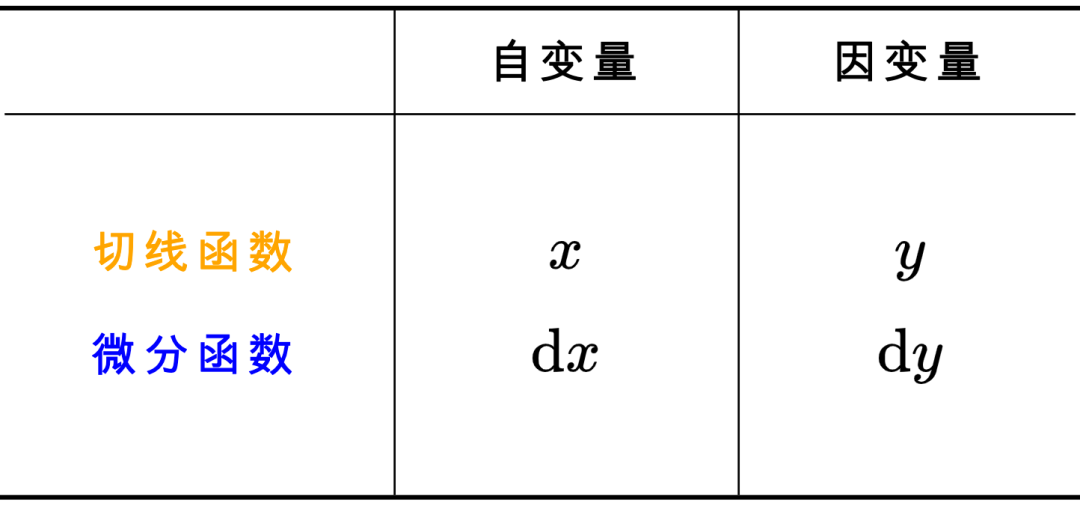
还有一个重大的区别:

摘自马同学图解单变量微积分
3.2 一直受困的细节
二维空间中可能有三维向量,比如下图中的  :
:

这是一个向量空间,它的 基 为:
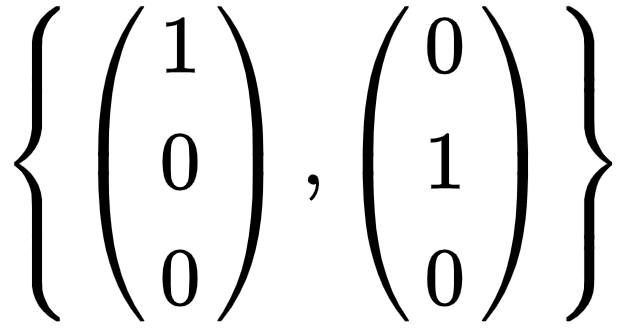
所以这是一个 2 维空间,但其中的向量为 3 维向量。
摘自马同学图解线性代数
4 有趣
如果能看懂内容,那么可以来关心下有趣这件事情了。
4.1 有趣的问题
如果这个知识能解决一些有趣的问题,那它本身也会有趣。比如古典派概率的知识可以解决下面这个问题
有次梅累骑士和朋友尼古拉斯(没有查到叫什么,估妄取一个,方便后面的讲述)打赌,赌注是64个金币。规矩是扔骰子,先扔出三次“6点”的话就梅累获胜,先扔出三次“4点”的话则尼古拉斯获胜:

玩了几次之后,战况如下,出现了两次“6点”,一次“4点”:

这个时候据说国王突然宣他们觐见,赌博只有中断,自然会产生一个问题:赌资如何分配?
尼古拉斯说,梅累只需要再出现一次“6点”就可获胜,而自己要出现两次“4点”才行,因此梅累应该获得两倍于自己的赌注,即按如下的比例来分配赌注:

梅累可不这么认为,他说自己只要再胜一次就可以通吃,而尼古拉斯要再胜一次才能和他平分秋色,所以他认为应该按照如下比例分配赌注:

这就是数学史上著名的 赌注分配问题(division of the stakes)。
摘自马同学图解概率与统计
4.2 生活的知识
如果数学知识可以和生活知识结合寄来,也会变得有趣。比如,教材中关于等价向量组的描述就是用色彩来描述的。
用颜色来解释上面的定理就是,既然  和
和  是等价向量组,那么
是等价向量组,那么  可以调出所有的颜色,所以
可以调出所有的颜色,所以  也可以调出来所有的颜色:
也可以调出来所有的颜色:
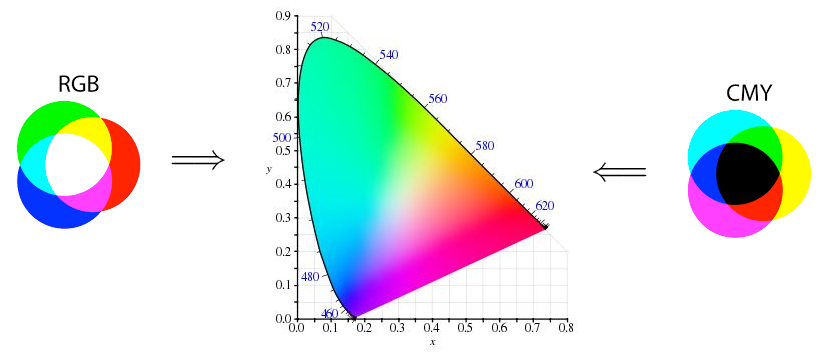
摘自马同学图解线性代数
4.3 应用
如果,在生产生活中可以应用所学的知识,也会让学习变得有趣。比如点积可以用来做书籍推荐。
下面是某书评网站,用户对一些书籍进行了相应的评分:

那么第一个用户信息可以用向量 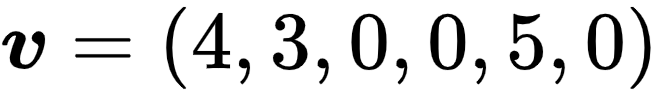 来表示。第二个的用户信息可以用向量
来表示。第二个的用户信息可以用向量  来表示。则它们的相似性就可以用余弦距离来表示:
来表示。则它们的相似性就可以用余弦距离来表示:

带入数据,结果保留到小数点后两位:

以此类推,我们就可以做出如下表格,表明各个用户的相似性:

这样就可以根据他们的相似性来进行书籍推荐了。
摘自马同学图解线性代数
5 结语
如果推荐一个有趣的高数、线代、概率教材,我推荐马同学图解系列。感兴趣的话可以通过下方的介绍购买。
我们通过通俗易懂、图形化的方式,对机器学习中的《监督式学习》进行了精讲,目前还在连载中,可以享受早鸟价格,可以点击下面的链接购买:
机器学习之《监督式学习》
???? 也可以直接点击下面这个图片购买机器学习的前置课程,《线性代数》、《单变量微积分》、《多变量微积分》、《概率论与数理统计》:

 最易懂的数学知识库:
最易懂的数学知识库:

马同学高等数学
看图学数学
微信公众号ID :matongxue314























 923
923

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








