剪邮票

剪邮票
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
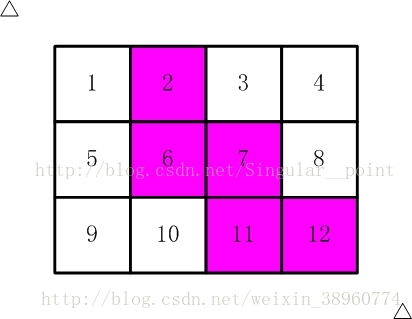
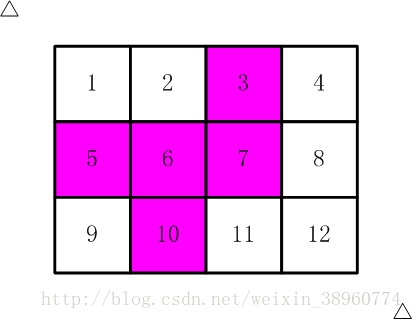
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

                                       第一种                                                                        第二种

格子问题，但是用回溯好像不行，因为每次的起点不一样； 
直接dfs也不行，因为dfs是一笔画，而有的5格一笔画是不行的，像第二种情况； 
可以先从小到大选取5个数字，保证不重复，然后判断这5个数是否连着；

要选取5个格子，必须要先设置一个数组保存5个格子的编号，因在原二维数组上是不能选的，然后可以用5个for，也可以回溯；

判断是从第一格子开始判断其上下左右是否有选中的格子，然后递归到那个格子，重复动作，可以bfs也可以递归；

先找到5个数的组合，然后从第一个数字开始遍历，经过上下左右操作检测5个数是否都被访问一遍，如果5个数都可以遍历到则种类+1。

在原图中向上为-4，向下为+4，向左为-1，向右为+1，但是遇到3 4 5 7 8这种4+1=5但是这种情况不符合，所以重构一下原图：

#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;

// 存储技巧
int grid[12] = {1,2,3,4,6,7,8,9,11,12,13,14};
int vis[15];
int knt;
queue<int> q;

void bfs(int i)
{
    int tot = 0;
    q.push(i);
    int temp;
    vis[i] = 0;
    while(!q.empty())
    {
        temp = q.front();
        q.pop();
        tot++;
        if(temp > 1 && vis[temp-1]) {q.push(temp-1); vis[temp-1] = 0;}
        if(temp > 5 && vis[temp-5]) {q.push(temp-5); vis[temp-5] = 0;}
        if(temp < 14 && vis[temp+1]) {q.push(temp+1); vis[temp+1] = 0;}
        if(temp < 10 && vis[temp+5]) {q.push(temp+5); vis[temp+5] = 0;}
    }
    if(tot == 5) knt++;
}


int main()
{
    for(int i = 0; i < 8; i++)
        for(int j = i+1; j < 9; j++)
            for(int k = j+1; k < 10; k++)
                for(int m = k+1; m < 11; m++)
                    for(int n = m+1; n < 12; n++)
        {
            memset(vis, 0, sizeof vis);
            vis[grid[i]] = 1;
            vis[grid[j]] = 1;
            vis[grid[k]] = 1;
            vis[grid[m]] = 1;
            vis[grid[n]] = 1;
            bfs(grid[i]);
        }
    printf("%d", knt);
    return 0;
}

#include <cstdio>
#include <cstring>

using namespace std;

int grid[13][2];
int cho[5];
int vis[5][6];
int sum;
int x, y;

int judge(int x, int y)
{
    if(!vis[x][y]) return 0;
    vis[x][y] = 0;
    return 1+judge(x, y-1)+judge(x-1, y)+judge(x, y+1)+judge(x+1, y);
}

// 因为要保存递增的五个值，id是第几个数，value是上一个数
void dfs(int id, int value)
{
    if(id == 5)
    {
        memset(vis, 0, sizeof vis);
        for(int i = 0; i < 5; i++)
        {
            x = grid[cho[i]][0];
            y = grid[cho[i]][1];
            vis[x][y] = 1;
        }
        if(judge(x, y) == 5) sum++;
    }
    else
    {
        for(int i = value+1; i < 13; i++)
        {
            cho[id] = i;
            dfs(id+1, i);
            cho[id] = 0;
        }
    }
}

int main()
{
    for(int i = 1, n = 1; i < 4; i++)
        for(int j = 1; j < 5; j++, n++)
        {
            grid[n][0] = i;
            grid[n][1] = j;
        }
    dfs(0, 0);
    printf("%d", sum);
    return 0;
}

#include<stdio.h>               直接做，不用变换标号
#include<string.h>
#include<math.h>
int map[3][4];
int flag[15];
int map_vis[3][4];   //标记数组
int s_flag[15];    //标记数组
int s[15];       //存所选的数
int dir[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
int sum=0,index=0;
void dfs1(int x,int y)
{                         //判断5个数是否相连
    int sx,sy;
       for(int i=0;i<4;i++)
       {
         sx=x+dir[i][0];
         sy=y+dir[i][1];
         if(sx<0 || sx>=3 || sy<0 || sy>=4)
            continue;                         //出界判断
         if(!s_flag[map[sx][sy]]|| map_vis[sx][sy])
           continue;
             map_vis[sx][sy]=1;
             index++;
             dfs1(sx,sy);
       }
}
void check()
{
    int x,y;
    memset(map_vis,0,sizeof(map_vis));
    memset(s_flag,0,sizeof(s_flag));
    int i;
    for(i=0;i<6;i++)
        s_flag[s[i]]=1;      
    for(i=0;i<12;i++)
    {
        x=i/4;
        y=i%4;
        if(s_flag[map[x][y]])    //找到所选的数在map数组中的位置
        {
            index=1;
            map_vis[x][y]=1;
            dfs1(x,y);
            break;
        }
    }
    if(index==5)
        sum++;
}
void dfs(int count)
{                         //列出从12个数中不重复选5个数的所有组合
    int i;
    if(count==6)
    {
          check();
        return;
    }
    else
    {
        for(i=s[count-1]+1;i<=12;i++)
        {
            if(!flag[i])
            {
                flag[i]=1;
                s[count]=i;     //将选好的5个数放到s数组中 
                dfs(count+1);
                flag[i]=0;
            }
        }
    }
}
int main()
{
    int i,j,k=1;
    for(i=0;i<3;i++)
        for (j=0;j<4;j++)
        map[i][j]=k++;
        dfs(1);
        printf("%d\n",sum);
    return 0;
}