适合32位及以下的单片机的开平方算法

你是不是觉得开平方直接调用C或Matlab内置sqrt就可以呢?这不是多此一举吗?

但是写单片机高速算法时,遇到你的算法周期总是快不起来呢?显示总卡屏呢?你机器总是很笨,反映不过来呢?没错,你的主体计算思路也许没错,就是卡在你调用的sqrt等函数上了,计算你的主体已经难以再精简了,那就有必要逐个有优化算法了.

比如:正余弦函数等,系统内置的都是泰勒展开式式计算

根据你需要选择合适的阶数嘛!非常正确,其它的呢?用泰勒原式嘛

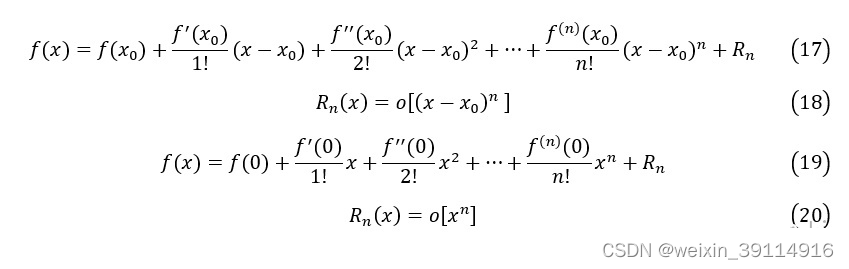
没错,我们的开平方也可以用泰勒展开式计算

因此泰勒开平方根的代码如下:

// c++ code
double ans=1, pre=0;
while(abs(ans-pre)>1e-6)

{
    pre=ans;
    ans=(ans+x/ans)/2;
}

这个精度有点高,可以算,但是这个也不是最快嘛!

本笔者用我们单片机最擅长的移位算法,分别得出两周计算步数最少的开整数方根的算法:

sqrt1(unit16 data)//快速开方
{unit16  pbta；
pbta=data>>1；
while(pbta^2>data)
{pbta=pbta>>1;
}
while(pbta^2<data)
{pbta++；
}
return pbta;
}
//bitshit(num，n)

再次申明,此算法仅仅适合于整数开整数方根,对精度要求高的高手,请用前面的算法.

解释权归"外号:十大爷",哈哈.