安卓如何实现多级结构树_数据结构-树（树基本实现C++）

最新推荐文章于 2024-04-14 13:07:18 发布
最新推荐文章于 2024-04-14 13:07:18 发布
阅读量164 收藏
点赞数
文章标签： 安卓如何实现多级结构树

49f4922b85076f21aa026818dbfd4633.png

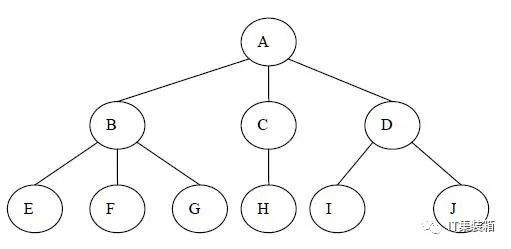
​树形结构是一种重要的非线性数据结构。其中树和二叉树最为常用，直观看来树是以分支关系定义的层次结构。树形结构是我们平时比较熟悉的，比如文件夹目录、公司组织关系等。在计算机领域也得到广泛的应用，编译程序就是以树来表示源程序的语法结构。

d315a46d8290af10009f474e3686ee23.png

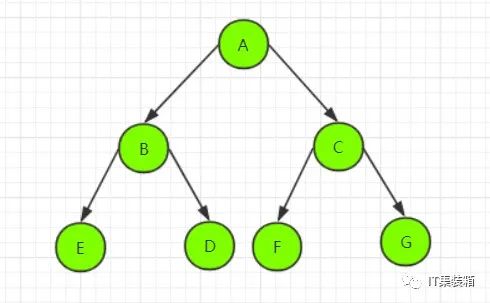
二叉树是一种特殊的树形结构，他的特点是每个节点至多只有两颗子树，并且，子树有左右之分，顺序不能颠倒。

c2686163eef20866305ed0a9dca59cd5.png

树形结构里边还有很多的知识点，我不在这里做文字上的解释，这里只是针对二叉树的相关特点，用C++分别实现基于数组和基于链表两种方式的二叉树，以及实现二叉树的三种遍历方式。
基于数组的二叉树基本实现：

#ifndef _CTREE_H_
#define _CTREE_H_
#include<iostream>

using namespace std;
//基于数组的二叉树基本实现
class Tree
{
public:
	explicit Tree(int size, int* pRoot)
	{
		m_iSize = size;
		m_pTree = new int[m_iSize];
		memset(m_pTree, 0, sizeof(int)*m_iSize);
		m_pTree[0] = *pRoot;
	}
	~Tree()
	{
		delete[]m_pTree;
		m_pTree = NULL;
	}
	int* SearchNode(int index)
	{
		if (index<0 && index>m_iSize)
		{
			return NULL;
		}

		return &m_pTree[index];
	}

	//direction 1:left 2:right
	bool AddNode(int index, int direction, int* pNode)
	{
		if (index<0 && index>m_iSize)
		{
			return false;
		}

		if (m_pTree[index] == 0)
		{
			return false;
		}

		if (index * 2 + direction > m_iSize)
		{
			return false;
		}

		m_pTree[index * 2 + direction] = *pNode;
		return true;
	}

	bool DeleteNode(int index, int* pNode)
	{
		if (index<0 && index>m_iSize)
		{
			return false;
		}

		*pNode = m_pTree[index];
		m_pTree[index] = 0;
		return true;
	}
	void Traverse()
	{
		for (int i = 0; i < m_iSize; i++)
		{
			cout << m_pTree[i] << " ";
		}
		cout << endl;
	}
private:
	int* m_pTree;
	int m_iSize;
};
#endif // !_CTREE_H_

基于链表的二叉树实现：

class TreeNode
{
public:
	int index; //坐标
	char data; //数据
	TreeNode *pLChild; //左节点
	TreeNode *pRChild; //右节点
	TreeNode *pParent; //父节点
public:
	TreeNode() : index(0), 
		data('0'), 
		pLChild(NULL), 
		pRChild(NULL), 
		pParent(NULL) {}

	TreeNode(int iNodeIndex, char val) : index(iNodeIndex), 
		data(val), 
		pLChild(NULL), 
		pRChild(NULL), 
		pParent(NULL) {}

	~TreeNode()
	{
		//if (pLChild)
		//{
		//	delete pLChild;
		//	pLChild = NULL;
		//}

		//if (pRChild)
		//{
		//	delete pRChild;
		//	pRChild = NULL;
		//}

		//if (pParent)
		//{
		//	delete pParent;
		//	pParent = NULL;
		//}
	}

	//TreeNode(const TreeNode& node)
	//{
	//	index = node.index;
	//	data = node.data;

	//	delete pLChild;
	//	if (node.pLChild)
	//	{
	//		pLChild = new TreeNode(node.pLChild->data, node.pLChild->index);
	//	}

	//	delete pRChild;
	//	if (node.pRChild)
	//	{
	//		pRChild = new TreeNode(node.pRChild->data, node.pRChild->index);
	//	}

	//	delete pParent;
	//	if (node.pParent)
	//	{
	//		pParent = new TreeNode(node.pParent->data, node.pParent->index);
	//	}
	//}

	//TreeNode& operator=(const TreeNode& node) 
	//{
	//	if (this == &node)
	//	{
	//		return *this;
	//	}

	//	index = node.index;
	//	data = node.data;

	//	delete pLChild;
	//	if (node.pLChild)
	//	{
	//		pLChild = new TreeNode(node.pLChild->data, node.pLChild->index);
	//	}
	//
	//	delete pRChild;
	//	if (node.pRChild)
	//	{
	//		pRChild = new TreeNode(node.pRChild->data, node.pRChild->index);
	//	}

	//	delete pParent;
	//	if (node.pParent)
	//	{
	//		pParent = new TreeNode(node.pParent->data, node.pParent->index);
	//	}

	//	return *this;
	//}

	TreeNode* SearchNode(int iNodeIndex)
	{
		if (index == iNodeIndex)
		{
			return this;
		}

		TreeNode *temp = NULL;
		if (pLChild)
		{
			if (pLChild->index == iNodeIndex)
			{
				return pLChild;
			}
			else
			{
				temp = pLChild->SearchNode(iNodeIndex);
				if (temp)
				{
					return temp;
				}
			}
		}
		if (pRChild)
		{
			if (pRChild->index == iNodeIndex)
			{
				return pRChild;
			}
			else
			{
				temp = pRChild->SearchNode(iNodeIndex);
				if (temp)
				{
					return temp;
				}
			}

		}

		return NULL;
	}

	void DeleteNode()
	{
		if (pLChild != NULL)
		{
			pLChild->DeleteNode();
		}

		if (pRChild != NULL)
		{
			pRChild->DeleteNode();
		}

		if (pParent != NULL)
		{
			if (this == pParent->pLChild)
				pParent->pLChild = NULL;
			if (this == pParent->pRChild)
				pParent->pRChild = NULL;
		}

		delete this;
	}

	//先序遍历 根左右
	void PreOrderTraversal()
	{
		cout << data << " ";

		if (pLChild)
		{
			pLChild->PreOrderTraversal();
		}

		if (pRChild)
		{
			pRChild->PreOrderTraversal();
		}
	}

	//中序遍历 左根右
	void InOrderTraversal()
	{
		if (pLChild)
		{
			pLChild->InOrderTraversal();
		}

		cout << data << " ";

		if (pRChild)
		{
			pRChild->InOrderTraversal();
		}
	}

	//后序遍历 左右根
	void PostOrderTraversal()
	{
		if (pLChild)
		{
			pLChild->PostOrderTraversal();
		}

		if (pRChild)
		{
			pRChild->PostOrderTraversal();
		}

		cout << data << " ";
	}

	//禁止拷贝、赋值
private:
	TreeNode(const TreeNode& node);
	TreeNode& operator=(const TreeNode& node);
};

//基于链表的二叉树基本实现和遍历
class CTree
{
public:
	CTree(TreeNode *pNode = NULL)
	{
		//创建树默认先创建根节点
		m_pRoot = new TreeNode();
		if (!m_pRoot)
		{
			throw "根节点申请内存失败";
			return;
		}

		if (pNode)
		{
			m_pRoot->index = 0;
			m_pRoot->data = pNode->data;
		}
		else
		{
			m_pRoot->index = 0;
			m_pRoot->data = '0';
		}
	}

	~CTree()
	{
		m_pRoot->DeleteNode();
	}

	TreeNode* SearchNode(int index)
	{
		return m_pRoot->SearchNode(index);
	}

	bool AddNode(int index, int direction, TreeNode *pNode)
	{
		if (!pNode)
		{
			cout << "插入失败！新增的节点值为空。" << endl;
			return false;
		}

		TreeNode *temp = SearchNode(index);
		if (!temp)
		{
			cout << pNode->data << "插入失败！找不到传入下标对应的父节点。" << endl;
			return false;
		}

		TreeNode *node = new TreeNode();
		if (!node)
		{
			cout << pNode->data << "插入失败！新的节点申请内存失败。" << endl;
			return false;
		}

		node->index = pNode->index;
		node->data = pNode->data;
		node->pParent = temp;

		if (1 == direction)
		{
			temp->pLChild = node;
		}
		else if (2 == direction)
		{
			temp->pRChild = node;
		}
		else
		{
			cout << pNode->data << "插入失败！。direction参数错误：1为左节点，2为右节点" << endl;
		}
		return true;
	}

	bool DeleteNode(int index, TreeNode *pNode)
	{
		TreeNode *temp = SearchNode(index);
		if (!temp)
		{
			cout << "删除失败！找不到传入下标对应的节点。" << endl;
			return false;
		}

		if (pNode)
		{
			pNode->index = temp->index;
			pNode->data = temp->data;
		}

		temp->DeleteNode();

		return true;
	}

	//先序遍历-递归
	void Recursive_PreOrderTraversal()
	{
		m_pRoot->PreOrderTraversal();
	}

	//中序遍历-递归
	void Recursive_InOrderTraversal()
	{
		m_pRoot->InOrderTraversal();
	}

	//后序遍历-递归
	void Recursive_PostOrderTraversal()
	{
		m_pRoot->PostOrderTraversal();
	}

	//先序遍历-非递归
	void PreOrderTraversal()
	{
		int stackTop = -1;
		TreeNode* nodeStack[10];
		TreeNode *pMove = /*new TreeNode(m_pRoot->index, m_pRoot->data)*/m_pRoot;
		while (stackTop != -1 || pMove)
		{
			while (pMove)
			{
				cout << pMove->data << " ";
				nodeStack[++stackTop] = pMove;
				pMove = pMove->pLChild;
			}

			if (stackTop != -1)
			{
				pMove = nodeStack[stackTop];
				stackTop--;
				pMove = pMove->pRChild;
			}
		}
	}


	//中序遍历-非递归
	void InOrderTraversal()
	{
		int stackTop = -1;
		TreeNode* nodeStack[10];
		TreeNode *pMove = /*new TreeNode(m_pRoot->index, m_pRoot->data)*/m_pRoot;
		while (stackTop != -1 || pMove)
		{
			//
			while (pMove)
			{
				nodeStack[++stackTop] = pMove;
				pMove = pMove->pLChild;
			}

			if (stackTop != -1)
			{
				pMove = nodeStack[stackTop--];
				cout << pMove->data << " ";
				pMove = pMove->pRChild;
			}
		}
	}

	//后序遍历-非递归
	void PostOrderTraversal()
	{
		int stackTop = -1;
		TreeNode* nodeStack[10];
		TreeNode* pMove = /*new TreeNode(m_pRoot->index, m_pRoot->data)*/m_pRoot;
		TreeNode* pLastVisit = NULL;

		while (pMove)
		{
			nodeStack[++stackTop] = pMove;
			pMove = pMove->pLChild;
		}
		while (stackTop != -1)
		{
			pMove = nodeStack[stackTop--];
			if (pMove->pRChild == NULL || pMove->pRChild == pLastVisit)
			{
				cout << pMove->data << " ";
				pLastVisit = pMove;
			}
			else
			{
				nodeStack[++stackTop] = pMove;
				pMove = pMove->pRChild;
				while (pMove)
				{
					nodeStack[++stackTop] = pMove;
					pMove = pMove->pLChild;
				}
			}
		}

	}
private:
	TreeNode *m_pRoot; //根节点
};

#endif // !_CTREE_H_

测试二叉树结构图：

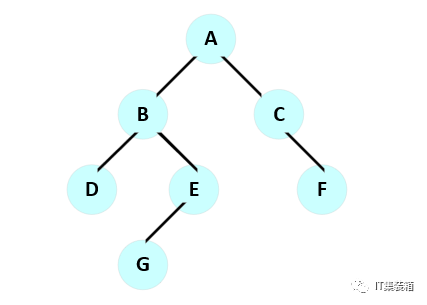
eae4401e832cd9f01281e30e95c663f0.png

测试主函数main.cpp实现：

#include "CTree.hpp"
#include <iostream>
using namespace std;
int main(int argc, char**argv)
{
	TreeNode nodeA(0, 'A');
	TreeNode nodeB(1, 'B');
	TreeNode nodeC(2, 'C');
	TreeNode nodeD(3, 'D');
	TreeNode nodeE(4, 'E');
	TreeNode nodeF(6, 'F');
	TreeNode nodeG(9, 'G');

	CTree *tree = new CTree(&nodeA);
	tree->AddNode(0, 1, &nodeB);
	tree->AddNode(0, 2, &nodeC);
	tree->AddNode(1, 1, &nodeD);
	tree->AddNode(1, 2, &nodeE);
	tree->AddNode(2, 2, &nodeF);
	tree->AddNode(4, 1, &nodeG);

	cout << "递归遍历: " << endl;
	cout << "先序遍历 根左右: " << endl;
	tree->Recursive_PreOrderTraversal();
	cout << endl;
	cout << "中序遍历 左根右: " << endl;
	tree->Recursive_InOrderTraversal();
	cout << endl;
	cout << "后序遍历 左右根: " << endl;
	tree->Recursive_PostOrderTraversal();
	cout << endl;

	cout << "非递归遍历: " << endl;
	cout << "先序遍历 根左右: " << endl;
	tree->PreOrderTraversal();
	cout << endl;
	cout << "中序遍历 左根右: " << endl;
	tree->InOrderTraversal();
	cout << endl;
	cout << "后序遍历 左右根: " << endl;
	tree->PostOrderTraversal();
	cout << endl;

	delete tree;

	system("pause");
	return 0;
}

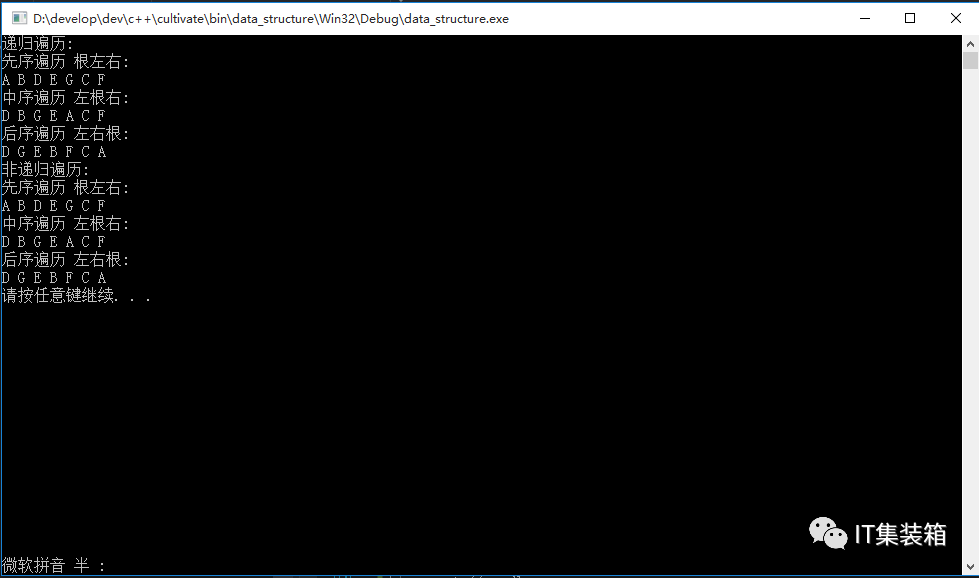
测试结果：

43b9f95e3725dcc42623c2c370666e2b.png


--|END|--

欢迎搜索个人WX公众号“IT集装箱”加关注，获取更多IT技术知识分享！

Android版数据结构与算法(十)：终极之树-红黑树与TreeMap详细解析
qq_16386581的博客
12-20 661
本文目录 一、为什么要创建红黑树这种数据结构 在上篇我们了解了AVL树，既然已经有了AVL这种平衡的二叉排序树，为什么还要有红黑树呢？ AVL树通过定义我们知道要求树中每一个结点的左右子树高度差的绝对值不超过1，其是一颗严格的平衡树，这样构建出来的平衡二叉排序树具有很好的查找性能，但是为了保持其每个结点平衡因子绝对值不超过1的特性在插入或者删除的时候需要的维护成本是很大的，插入或者删除需要大量的...
Android-listview实现多级树列表（文件夹目录结构和企业级通讯录结构）
AFinalDream
04-09 3047
企业级的通讯录，我们把企业级的通讯录做成多级树结构，并且做到分步加载。使用listview，实现单选、多选、侧滑等情况下的通讯录。
Android树形结构列表
02-25
Android树形结构列表
Android版数据结构与算法(六):树与二叉树
weixin_30301183的博客
10-08 152
版权声明：本文出自汪磊的博客，未经作者允许禁止转载。 之前的篇章主要讲解了数据结构中的线性结构，所谓线性结构就是数据与数据之间是一对一的关系，接下来我们就要进入非线性结构的世界了，主要是树与图，好了接下来我们将会了解到树以及二叉树，二叉平衡树，赫夫曼树等原理以及java代码的实现，先从最基础的开始学习吧。 一、树 树的定义： 树是n(n>=0)个结点的有限集合。 当n=0时，集合...
android树形菜单，树形结构，多级展示
07-24
树形菜单，用来展示有层次结构的数据，像文件管理器，一个文件夹下面有很多文件，文件夹，可能文件夹下面还有文件还有文件夹。我们需要展示这些结构，但是安卓并没有提供一个比较方便的控件来展示,所以就需要我们自定义。博客详解:http://blog.csdn.net/wangjie1310/article/details/47026937
android treeview 树形结构,前端开发中，使用TreeView控件创建树形结构
weixin_39878991的博客
05-31 800
原标题：前端开发中，使用TreeView控件创建树形结构Wijmo是一款使用Type编写的新一代Java/HTML5控件集。它秉承触控优先的设计理念，在全球率先支持AngularJS，并提供性能卓越、零依赖的FlexGrid和图表等多个控件。我们已经知道在Wijmo 2017V1版本中新增了TreeView控件，那么如何使用这个控件来创建树呢？下面小编来告诉大家。入门使用TreeView控件就像使...
C++语言实现一个多级文件目录管理系统，采用链表的数据结构。.zip
01-15
软件开发设计：应用软件开发、系统软件开发、移动应用开发、网站开发C++、Java、python、web、C#等语言的项目开发与学习资料 硬件与设备：单片机、EDA、proteus、RTOS、包括计算机硬件、服务器、网络设备、存储设备...
mysql 定义多级表头_js treeData 树形数据结构 无限层级(转载)
weixin_39615402的博客
02-18 484
js实现无限层级树形数据结构(创新算法)转载：https://blog.csdn.net/Mr_JavaScript/article/details/82817177由于做项目的需要，把一个线性数组转成树形数组，在网上查了很多文章，觉得他们写的太复杂了，于是自己写了一个，在折腾了一下午终于把它写出来啦(激动.gif)，用两个filter过滤器就搞定了，代码简洁明了，数据结构小白都能看懂。js代码：...
右击树形控件实现节点动态添加删除修改（VC 6.0实现）
08-01
以上就是使用VC 6.0实现树形控件动态添加、删除和修改节点的基本步骤。这个程序可以帮助初学者理解MFC中与树形控件交互的原理，同时也能锻炼事件处理和用户界面交互的设计能力。在实际应用中，你可能还需要考虑更多...
Android 打造任意层级树形控件 考验你的数据结构和设计
最新发布
2401_84121958的博客
04-14 811
===大家在项目中或多或少的可能会见到，偶尔有的项目需要在APP上显示个树形控件，比如展示一个机构组织，最上面是boss，然后各种部门，各种小boss，最后各种小罗罗；整体是一个树形结构；遇到这样的情况，大家可能回去百度，因为层次多嘛，可能更容易想到ExpandableListView ， 因为这玩意层级比Listview多，但是ExpandableListView实现目前只支持两级，当然也有人改造成多级的；但是从我个人角度去看，首先我不喜欢ExpandableListView ，数据集的组织比较复杂。
android自定义绘制二叉树,安卓数据结构04-二叉树
weixin_32540913的博客
05-25 256
数据结构04-二叉树一、树的基本概念1.树树是n(n>=0)个节点的有限集。n=0时称为空树。在任意一颗非空树中：有且仅有一个特定的称为根(Root)的节点；当n>1时，其余节点可分为m(m>0)个互不相交的有限集T1、T2、......、Tm，其中每一个集合本事又是一颗树，并且称为根的子树(SubTree)。2.度节点的度是节点拥有的子树数。度为0的节点称为叶子节点或终端节点，...
android递归树形结构,c#通用递归生成无限层级树
weixin_29488835的博客
05-31 152
public void LoopToAppendChildren(List all, NewsType curItem){var subItems = all.Where(ee => ee.ParentId==curItem.Id).ToList();curItem.children = new List();curItem.children.AddRange(subItems);fore...
数据结构封装之《GTree通用树》
BeiJiaan的博客
09-03 1969
学习记录
android多级树形列表
2401_84010816的博客
04-04 1022
外链图片转存中…(img-Ky7EuBUK-1712217038052)][外链图片转存中…(img-hASIMV2c-1712217038053)][外链图片转存中…(img-a0J6fJ2S-1712217038054)][外链图片转存中…(img-xLh2Qx4m-1712217038054)][外链图片转存中…(img-awH2n01S-1712217038054)]
android 组织架构列表,android开发学习系列【壹】组织架构及信息传递
weixin_39518002的博客
06-03 172
今天又有了一点新的收获，写给自己也照亮有缘人。写程序断断续续也有七八年的时间了，原来是按照例程抄写，实现功能。有了C++的基础再去学习其他语言当然感觉更加轻松。如果抄写示例程序，编译运行都是没有问题的。出现问题的地方在于，我想在例子的基础上做相应的删减和增加就不是很顺利了。静下来想想，为什么呢？想来可能是由于对要删减的模块和整体的联系没有理清，导致删的不够彻底。删除该功能后却有其他模块依然要使用此...
用Java简单实现部门多叉树
weixin_39997438的博客
07-12 965
树是一个非常关键的数据结构，在我们日常的开发中，它能帮助我们解决很多问题。例如：一个公司有多个部门，每个部门的结构也都不同，有些部门底下直接对接对应的岗位，而有些部门比较大，其底下可能存在多个小部门。对于这种情况，数据结构【树】完美的贴合了该情景...
安卓逆向_1 --- 逆向环境配置、APK 文件结构、APK 打包流程
墨鱼菜鸡
07-11 2224
哔哩哔哩：https://www.bilibili.com/video/BV1UE411A7rW?p=1 Android 逆向工程师系统培训‹第九期›( 课程目录 )：https://ke.yijincc.com/course-21.htm 安卓逆向工程师：https://ke.yijincc.com/profession/1.htm 打造年轻人的...
android多级树形结构列表(完整代码，可以选择某项)
热门推荐
奋斗
08-07 2万+
多级列表是个很常见的功能，发现很多代码都不好扩展，或者由于数据结构设计不好，导致开发维护比较费时间。下面自己写了一个，github连接地址： github地址分享一波。如图所示 看一下节点的代码，最重要的设计TreePoint public class TreePoint { private String ID; // 7241, //账号i...
Android 多级部门树（支持无限级），支持部门级别多选
03-14
需要的同学，绝对物有所值，不会让同学们失望
android源码树结构介绍
张晖的专栏
05-01 4633
最近在学习android源码，在这里分享学习过程中总结的一些知识。仅供参考，如有错误，还请指教。无论是下载源码还是在AndroidXref 上在线阅读源码，我认为首先都要弄明白源码中各个目录下的代码所负责的工作，以nougat 7.1.1_r6为例，其源码树目录结构如下 下面就来介绍一下各部分的作用：bionic这是google专为android开发的一套c标准库，采用bsd许可形式开源，go
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值
>