spss正态性检验_参数检验与非参数检验如何用？

1、 参数检验——两个独立样本

什么是独立样本？

将研究对象随机的分配到两组中，分别接受不同的处理，或分别从两个总体中完全随机的抽取一部分个性进行研究，这样的样本就是独立样本。相应的T检验就是独立样本T检验。

什么时候运用参数检验，什么时候运用非参数检验呢？

需要进行正态性检验，服从正态分布则使用参数检验，不服从正态分布则使用非参数检验。

例如：比较英语专业和非英语专业的英语成绩是否存在显著的差异性

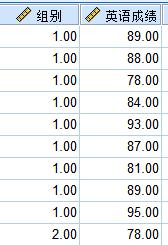
正态性检验：

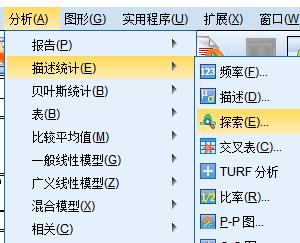
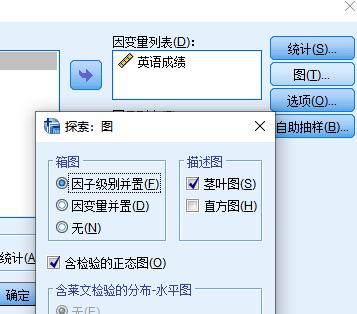
说明符合正态分布，于是选择参数检验。

SPSS软件进行独立样本T检验：

分析——比较均值——独立样本T检验——

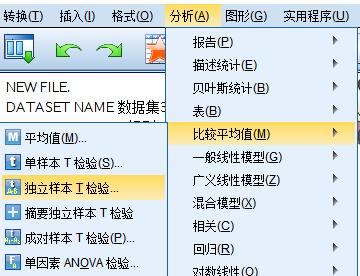
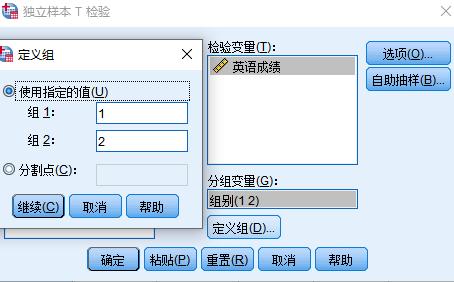
结果如下：

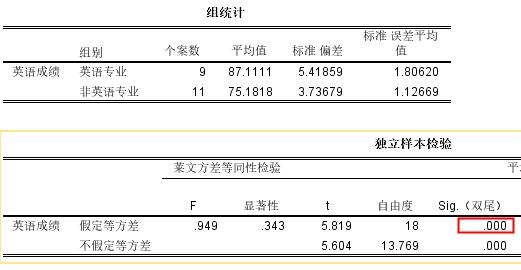
从图表可以看出，显著性是0.000，非常显著的，且英语专业英语成绩的均值是87，非英语专业的英语成绩均值是75，说明成绩是显著差异的。

2、 非参数检验——两个独立样本

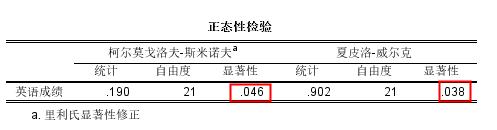
当正态性检验结果显示不符合正态分布时，则选择非参数检验。

SPSS非参数检验默认的是Mann-Whitney U 法。

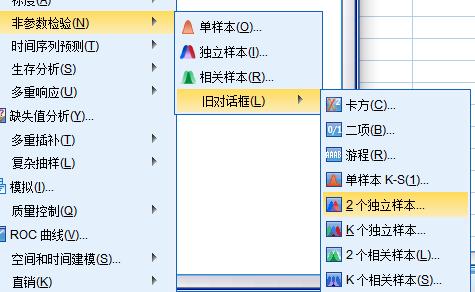
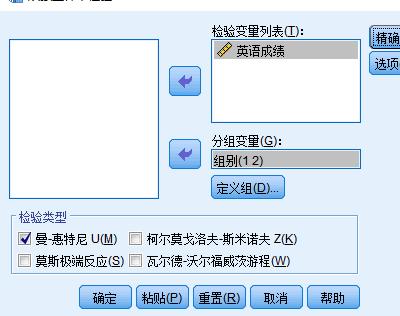
结果输出如下

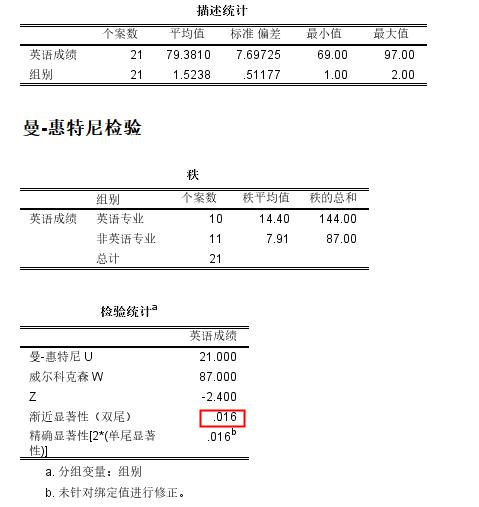
从图可以看出，显著性是0.016，是有统计学意义的。