# 异运算_异分母分数加减法的计算技巧(附练习题）

异分母分数加减法的计算技巧

异分母分数加减法因为要先通分，所以计算时往往用时长、出错多。其实在计算过程中还是有许多窍门可寻的，如果利用得当，多数题目都可以达到口算的程度。

异分母分数加减法的关键是通分，如何快速的找到两个或多个分母的公分母就显得格外重要。我们一般情况下选择两个分母的最小公倍数作公分母。首先把不同的分母进行分类，这里我们先以两个分母为例。可以把不同的分母分为三类：1.互质关系，2.倍数关系，3.普通关系。在找两个分母公分母的时候，先来观察它们属于哪一类。当两个分母属于互质关系时，两个分母的乘积就是公分母。例如，公分母就是20。当两个分母属于倍数关系时，较大的数就是公分母。例如，公分母就是6。当两个分母既不是互质关系，又不是倍数关系时，我们称为普通关系。普通关系找公分母可以用大数翻倍法。例如，我们用8先乘2等于16，发现16不是6的倍数，再用8乘3等于24，发现24是6的倍数，所以公分母就是24。快速的确定了公分母就可以用分数的基本性质进行通分计算了。

在异分母分数加减法口算中最常见的是分子是1分母互质的，课本中涉及到了这类规律。如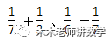：，此类题目的口算方法是：分母的乘积作分母(因为两个分母互质)，分母的和或差作分子(小学阶段不涉及负数加减法，分母的差默认为大数减小数)。所以，分母7×3=21，分子7+3=10。，分母6×7=42，分子7－6=1。而且这一类的计算结果一定是最简分数，不需要约分。

除了分子是1分母互质的以外，分子不是1，分母互质的我们也可以总结窍门。分母仍然是两个分母的乘积，分子大家可以记“交叉相乘”，就是用交叉相乘的积作分子。例如，分母3×8=24，分子2×8=16、3×5=15、16+15=31。

其实，如果分母不互质的情况下，也可以运用“交叉相乘”的方法进行计算，只不过计算结果一定需要约分，有的时候比正常通分还要简单，大家可以根据具体情况灵活把握。例如：，我们也可以用6×8=48作分母，6+8=14作分子，最后约分即可。再如：，我们也可以用4×6=24作分母,5×4=20、3×6=18、20－18=2作分子，最后约分即可。

对于分数的连加连减、加减混合，如果有同分母的，我们可以运用加法的运算律和减法的性质把同分母的分数先进行计算，达到简算的目的。如：就可以运用交换律，再如：就可以运用减法的性质。

对于分母是倍数关系的，因为公分母是较大的数，所以通分过程中只需要变化一个分数，相对口算起来能简单一些，而普通关系因为找公分母比较复杂，绝大多数情况下建议同学们先通分再计算。

附一份异分母分数加减法专项练习，需要的亲可以长按下载。