matlab进行图像降维,KLT降维与图像压缩（附MATLAB代码）

KLT简述

KLT (Karhunen-Loeve Transform) 是变换编码 (Transform Coding) 的一种方法，它可以将数据转化为更利于压缩的一种形式，去除数据相关性形成的冗余。KLT通常也称为PCA (Principal Component Analysis) 或者EVD (Eigenvalue Decomposition), 在不一样的课程和教材中它们可能有一些差异，但本文将要讲的图像压缩中的KLT指的就是计算图像协方差矩阵，保留较大的特征值和其对应的特征向量的方法。html

步骤原理

首先将待处理的图像分割成n个M

×

N

M\times NM×N 的图像块，并将图像块中数据按照从左到右，从上到下的顺序从新排列成一个列向量，每个列向量长度为M

×

N

M\times NM×N，共有N

T

N_{T}NT​个这样的列向量，第i

ii个列向量为x

n

i

\bm{x}_{ni}xni​

以二维向量为例，假设每个向量能够表示为[

x

1

,

x

2

]

T

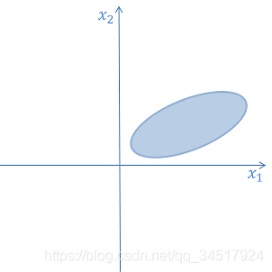
\left [x_1,x_2 \right ]^T[x1​,x2​]T,那么能够将这些数据点表示在二维平面内，以下图所示，椭圆内为二维向量分布点。web

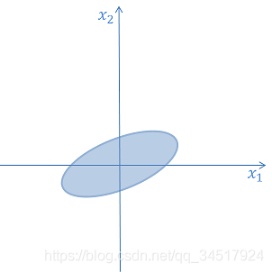
数据中心化：x

=

x

n

i

−

x

ˉ

\bm{x}=\bm{x}_{ni}-\bar{\bm{x}}x=xni​−xˉ ，其中x

ˉ

\bar{\bm{x}}xˉ为全部列向量的均值。能够看做将数据集平移至原点。app

计算协方差矩阵C

\bm{C}Cide

C

=

E

[

x

x

T

]

=

E

[

(

x

n

i

−

x

ˉ

)

(

x

n

i

−

x

ˉ

)

T

]

\bm{C}=E\left [\bm{x}\bm