r语言 求几个数的最小公倍数_【微课】北师大版五年级数学上册第五单元8找最小公倍数...

教材内容：教材81～82页的内容。

本节课的内容是在学生掌握了“倍”的基础上学习的，主要是为分数的大小比较和通分奠定基础。

复习旧知

1.因数和倍数的意义：

在a×b＝c(a，b，c是不为0的自然数)中，a和b是c的因数，c是a和b的倍数。

2.找一个数的倍数的方法：

用这个数(非0自然数)和任意一个自然数(0除外)相乘，所得的积都是这个数的倍数。

知识与技能

1.理解公倍数和最小公倍数的意义。

2.会用列举法等方法找两个数的公倍数和最小公倍数。

过程与方法

通过圈一圈、看一看、说一说等活动，让学生经历探究找最小公倍数的过程，从而理解公倍数、最小公倍数的意义，培养学生自主发现问题、分析问题、解决问题的能力。

情感、态度与价值观

1.在学习活动中，感受数学知识的奥妙，激发学习数学知识的兴趣，培养热爱数学的良好情感。

2.结合生活实际，激发学生探究生活中数学问题的欲望，培养学生主动探究的意识。

重点：

理解公倍数和最小公倍数的意义，掌握找最小公倍数的方法。

难点：

能正确找出每组数的最小公倍数。

1 公倍数和最小公倍数的含义

问题导入　在下表中用“○”标出4的倍数，用“△”标出6的倍数。(教材81页例题)

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50

1.分别找出4和6的倍数

方法一　先在表中用“○”标出4，然后每隔3个数再标出一个数，这些数都是4的倍数；再用同样的方法，在表中用“△”标出6，然后每隔5个数再标出一个数，这些数都是6的倍数。

方法二　根据求一个数倍数的方法，先用4分别乘1，2，3，4，5，…求出4的倍数，在表中用“○”标出；再用同样的方法，用6分别乘1，2，3，4，5，…求出6的倍数，在表中用“△”标出。如下图：

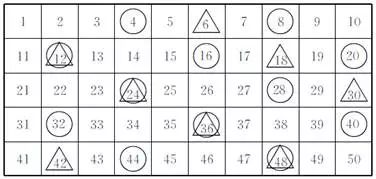
从表中可知：

50以内4的倍数有4，8，12，16，20，24，28，32，36，40，44，48。

50以内6的倍数有6，12，18，24，30，36，42，48。

2.明确公倍数和最小公倍数的含义

在表中既标有“○”又标有“△”的数是12，24，36，48。它们是4和6公有的倍数，也就是它们的公倍数，其中12是最小的一个，它是4和6的最小公倍数。

3.观察4和6的公倍数，发现公倍数的特征

(1)一个数的倍数的个数是无限的，因此两个数或三个数的公倍数的个数也是无限的，只有最小的公倍数，没有最大的公倍数。

(2)几个数的公倍数是这几个数最小公倍数的倍数，几个数的最小公倍数是这几个数的公倍数的因数。

例如：4和6的公倍数24是4和6的最小公倍数12的倍数，4和6的最小公倍数12是4和6的公倍数24的因数。

4.明确公倍数的表示方法

方法一　列举法。

4和6的公倍数有12，24，36，…

4和6的最小公倍数是12。

方法二　集合法。

归纳总结：

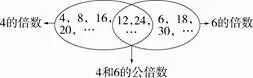
几个数公有的倍数，叫作这几个数的公倍数。

其中最小的一个，叫作它们的最小公倍数。

2 求最小公倍数的方法

问题导入　求10和15的最小公倍数。

1.探究求10和15的最小公倍数的方法

方法一　列举法。

(1)方法分析。

根据最小公倍数的含义，先找出10的倍数，再找出15的倍数，然后找出10和15的公倍数，最后从中找出最小公倍数。

(2)正确解答。

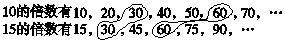
10和15的最小公倍数是30。

方法二　试除法。

(1)方法分析。

先写出15的倍数，再把15的倍数按从小到大的顺序依次除以较小数10，第一个能被10整除的数就是10和15的最小公倍数。

(2)正确解答。

15的倍数有15，30，45，60，75，…

15的倍数中是10的倍数的有30，60，…

10和15的最小公倍数是30。

2.特殊数的最小公倍数的求法

(1)成倍数关系的两个自然数的最小公倍数是较大数，例如：3和12的最小公倍数是12。

(2)只有公因数1的两个数的最小公倍数是这两个数的积，例如：7和9的最小公倍数是63。

归纳总结：

求两个数的最小公倍数的方法：

(1)列举法：先分别写出两个数各自的倍数，再从中找出公倍数和最小公倍数；

(2)试除法：先写出两个数中较大数的倍数，再把这些数按从小到大的顺序依次除以较小数，第一个能被较小数整除的数就是它们的最小公倍数。

拓展提高

1.求三个或三个以上数的最小公倍数的方法，与求两个数的最小公倍数的方法相同，可以用列举法。

2.用短除法求两个数的最小公倍数。

例如：求18和24的最小公倍数。

找出18和24的公因数2，用2去除18和24，看它们的商是否只含有公因数1，如果只含有公因数1就不用再除了，如果除了1还有别的公因数就继续除，然后把除数和所得的商连乘起来就是18和24的最小公倍数。如下所示：

所以18和24的最小公倍数是2×3×3×4＝72。

易错易混

误区一

填空：3和6的最小公倍数是(18)。

错解分析

3的倍数有3，6，9，12，15，18，…

6的倍数有6，12，18，…

6是3的倍数，所以6的所有倍数都是3的倍数。

错解改正　6

温馨提示

当较大数是较小数的倍数时，这两个数的最小公倍数就是较大数。

误区二

选择：两个数的最大公因数是1，最小公倍数是35，这两个数分别是(C)。

A.5和7　　　　B.15和20　　　　C.35和5

错解分析

虽然35和5的最小公倍数是35，但它们的最大公因数是5，不是1。

错解改正　A

温馨提示

解答此类问题，既要考虑最小公倍数，又要考虑最大公因数。

思考：

一些小朋友分组做游戏，第一次分组每组4人余下2人，第二次分组每组5人也余下2人。你知道最少有多少个小朋友做游戏吗？

觉得好看，请点这里↓↓↓