四个角不是直角的四边形_一线三等角构造全等——解析2020黑龙江中考数学26题（压轴题）...

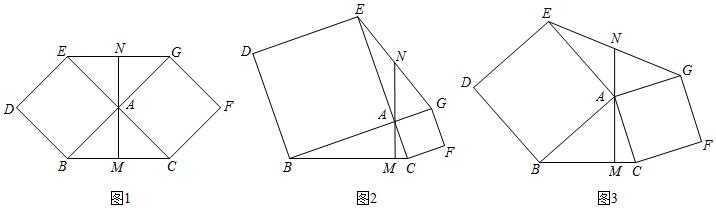
(2020•黑龙江-26)以Rt△ABC的两边AB、AC为边，向外作正方形ABDE和正方形ACFG，连接EG，过点A作AM⊥BC于M，延长MA交EG于点N．

(1)如图①，若∠BAC＝90°，AB＝AC，易证：EN＝GN；

(2)如图②，∠BAC＝90°；如图③，∠BAC≠90°，(1)中结论，是否成立，若成立，选择一个图形进行证明；若不成立，写出你的结论，并说明理由．

试题动画制作讲解链接：观看试题图形制作视频请戳我

试题分析讲解链接：观看试题分析视频请戳我

【分析】

(1)由等腰直角三角形的性质得出∠MAC＝45°，证得∠EAN＝∠NAG，由等腰三角形的性质得出结论；

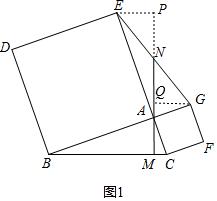
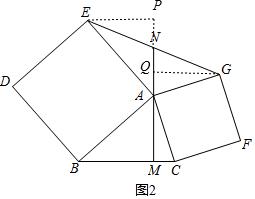
(2)如图1，2，证明方法相同，利用“AAS”证明△ABM和△EAP全等，根据全等三角形对应边相等可得EP＝AM，同理可证GQ＝AM，从而得到EP＝GQ，再利用“AAS”证明△EPN和△GQN全等，根据全等三角形对应边相等可得EN＝NG．

【解析】

(1)证明：∵∠BAC＝90°，AB＝AC，

∴∠ACB＝45°，

∵AM⊥BC，

∴∠MAC＝45°，

∴∠EAN＝∠MAC＝45°，

同理∠NAG＝45°，

∴∠EAN＝∠NAG，

∵四边形ABDE和四边形ACFG为正方形，

∴AE＝AB＝AC＝AG，

∴EN＝GN．

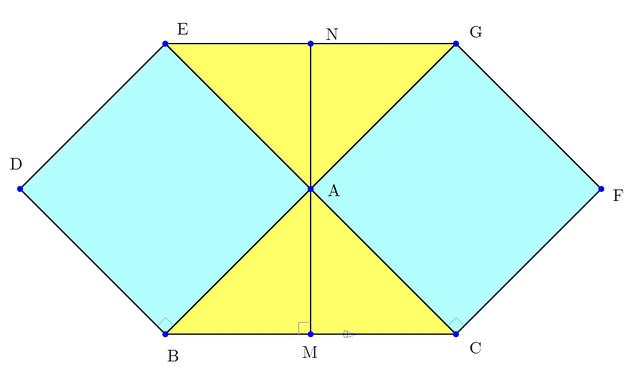
(2)如图，∠BAC＝90°时，

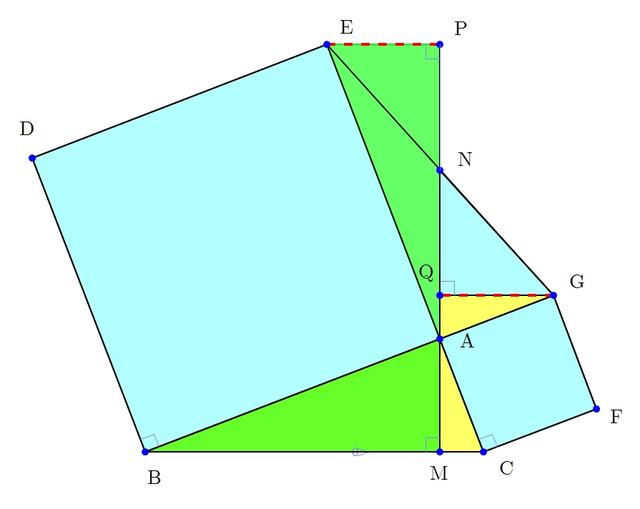
借助一线三等角的基本模型构造全等

(1)中结论成立．

理由：过点E作EP⊥AN交AN的延长线于P，过点G作GQ⊥AM于Q，

∵四边形ABDE是正方形，

∴AB＝AE，∠BAE＝90°，

∴∠EAP+∠BAM＝180°﹣90°＝90°，

∵AM⊥BC，

∴∠ABM+∠BAM＝90°，

∴∠ABM＝∠EAP，

∴△ABM≌△EAP(AAS)，

∴EP＝AM，

同理可得：GQ＝AM，

∴EP＝GQ，

∴△EPN≌△GQN(AAS)，

∴EN＝NG．

证法二：

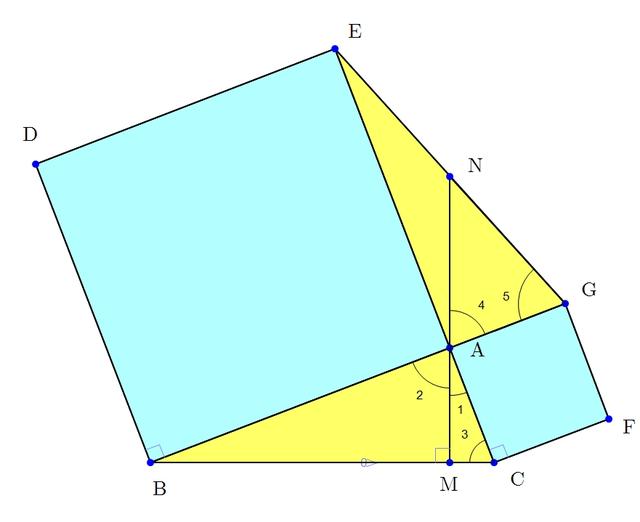
借助角的同余关系证明EN=AN=NG

如图，∠BAC＝90°时，也可以借助，△ABC≌△AEG(SAS)可得∠3=∠5,以及，

∵∠1+∠2＝90°，∠1+∠3＝90°

∴∠3=∠2，又∠4=∠2

∴∠4=∠5

……

易证：EN＝NG

如图，∠BAC≠90°时，

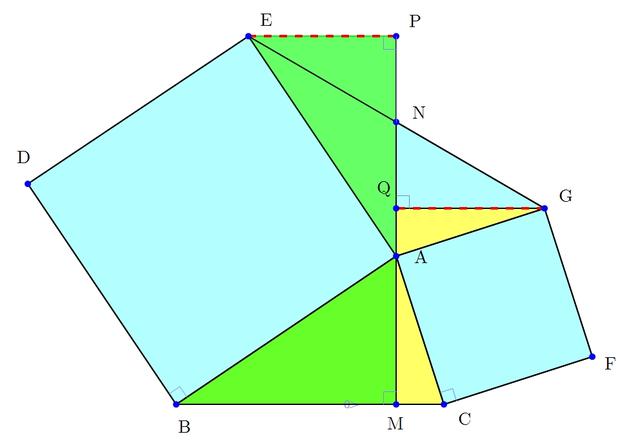
(1)中结论成立．

理由：过点E作EP⊥AN交AN的延长线于P，过点G作GQ⊥AM于Q，

∵四边形ABDE是正方形，

∴AB＝AE，∠BAE＝90°，

∴∠EAP+∠BAM＝180°﹣90°＝90°，

∵AM⊥BC，

∴∠ABM+∠BAM＝90°，

∴∠ABM＝∠EAP，

∴△ABM≌△EAP(AAS)，

∴EP＝AM，

同理可得：GQ＝AM，

∴EP＝GQ，

∴△EPN≌△GQN(AAS)，

∴EN＝NG．

喜欢我的分析的亲们，记得关注我的头条号：龙老师数学工作室，一定多多分享；

西瓜视频里搜索：龙老师数学工作室，有更多视频，分析各省市中考压轴题，动图制作技巧的讲解，以及制图软件——几何表达式使用教程合集……