直角三角形的边角关系_全等三角形判定之边角边定理的运用，学习证明题的证明思路...

全等三角形的判定中，边角边定理的运用也是边、角存在等量关系时，常用到的判定方法，边角边定理的内容是，两边和它们的夹角对应相等的两个三角形全等，简写成“SAS”，它的书写格式，在列举两个三角形全等的条件时，一般把夹角写在中间，以突出两边及其夹角对应相等。需要特别注意的是，利用“SAS”判定两个三角形全等时，必须满足“两边及其它们的夹角”这一条件，书写的时候，按照“边角边”的顺序书写。注意有两边和其中的一角对应相等的两个三角形不一定全等。

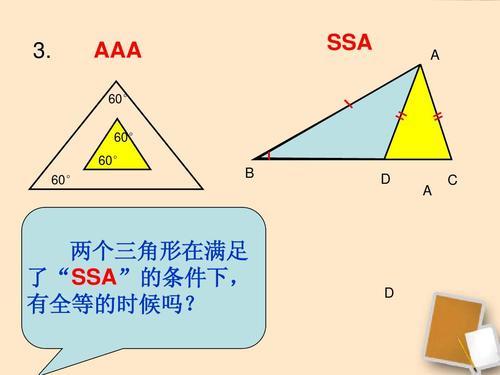
例题：如图，在直角三角形ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB。(1)、求∠CAD的度数，(2)、延长AC至E，使CE=AC，求证：DA=DE.

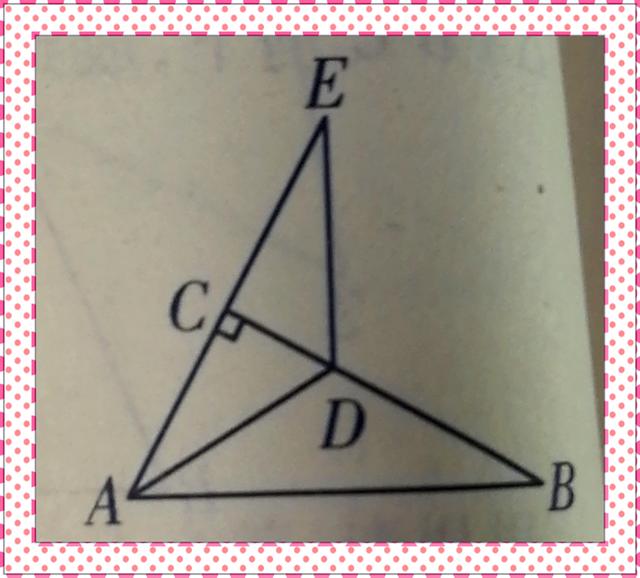
【解析】：(1)、利用直角三角形中两个锐角互余的性质和角平分线的性质进行解答；已知在Rt△ABC中，∠ACB=90°,∠B=30°，所以∠CAB=60°，又已知AD平分∠CAB，所以∠CAD=∠DAB=30°，即∠CAD=30°。(2)、要证边或角相等，只要证它们所在的三角形全等即可。已知∠ACB=90°，所以∠ACD=90°，∠ECD=90°，则∠ACD=∠ECD，又已知AC=EC，所以在ACD与∠ECD中，AC=EC，∠ACD=∠ECD，CD=CD，所以△ACD≌△ECD(SAS)，所以DA=DE。

在做证明题的时候，经常会用到分析法来寻找证明思路，上题中，就是运用了分析法寻找证明思路，所谓的分析法就是执果索因，由未知看需知，思维方式上就是从问题入手，找能求出问题所需要的条件或可行思路，若问题需要的条件未知，则把所需条件当作中间问题，再找出解决中间问题的条件。以此类推，最终找寻到已知条件，或者是定理等。除了逐渐学会证明题的证明思路，在对全等三角形进行判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造全等三角形，对于辅助线的添加，也是学习过程中，需要掌握的。

希望同学们将几个判定定理，每一个都分析透彻，在做题中，才能够得心应手。