本文从希尔伯特空间的角度探讨线性变换，解释了变换的三大核心问题：参考系统、元素的线性表达和相似性计算。通过对傅里叶变换的分析，阐述了线性变换的思想，指出理解线性变换的关键在于完备的线性空间、基函数的选择和内积的定义。同时，文章揭示了不同变换如傅里叶、小波变换等在处理信号和图像时的优缺点，强调寻找更优基函数以实现数据的稀疏表达是当前挑战之一。
一般线性变换以及傅里叶变换，欧氏变换，仿射变换，余弦变换，小波变换，拉普拉斯变换，Z变换，希尔伯特变换等等这些所谓的变换太多了，这些到底搞得是什么？怎么像云像雾又像风呢？怎么才能彻底理解它们？它们究竟解决什么问题？这个问题目前到底解决的怎么样了？下面引用两个教师的感慨：第一个老师说：我退休后一个最大的愿望就是搞清楚线性代数到底讲的是啥？特征值，特征向量到底怎么回事，看书好像理解了，放下书好像又什么也没有理解，糊里糊涂，以后退休了一定要好好学习一下线性代数，一定搞清楚到底是什么，了却自己的心愿；另外一个老师说：我是一个好好学习的学生，学习的是工程方面的专业，希望自己能够成为一个有成就的科技工作者，可是一学习到傅里叶变换，什么时域和频域变换，就糊涂了，迷失了自己，从此不能自拔，最后放弃做科研工作了。
很容易理解第一位教师的感慨，做了教师，一天到晚忙着教学，而教学的内容也不太涉及线性代数的知识，就是涉及到，也可以依葫芦画瓢将教材的内容讲清楚，但是感觉总是缺少点什么，知其然不知道所以然，本打算仔细学习线性代数，但是没有时间和精力，就是很下心学一段时间，仍然不得要领。对于第二位老师的感慨，确实很多人被这时域和频域搞得头昏，以为自己没有科研天赋，从此告别科研工作，选择其它道路了。
到底怎么回事，这些所谓的变换概念到底是什么？搞得人们似乎懂了，可是一转身又感觉什么也不懂呢！其实这是普通大学培养体系里面急功近利造成的。工科大学培养的出发点是工匠而不是工程师，结果是理论体系不充分，知识结构不完备，那就很难理解线性变换了。事实上，任何理工科大学本科生必须认真学习完傅里叶分析，复分析，实分析和泛函分析，否则根本没有能力彻底理解线性变换的思想，而在上研究生阶段时，一般学过这四门课程，可是课堂上讲的都是该门课程教材前3章的内容，主要内容没涉及到，使得学生误以为自己学完了这些课程的全部内容，其实这还不如不学，不学还能想起来认真学一下，而课堂上正规教学却只学一点，学生以为都学完了，就没有再深入学习的计划和想法，这才是最害人的。我们下面一点点讲述，试图彻底讲清楚，同时给出一些变换的局限性和未来的发展思路，这仅仅是个人的理解，其中理解可能是错误的，欢迎看到的读者指正，同时也希望读者批判的看这些理解，以怀疑的态度对待它。
使用数学工具描述客观世界，这是人类认识，理解和运用客观事物的前提，当然描述这个客观世界的数学工具越是简单越好，但简单不是粗略，而是要求精确的同时简单。那么简单就意味着参数少，同时尽量使用初等函数。如果我们能够使用参数少而且简单的初等函数描述这个客观世界，那将是多么令人激动的事情，事实上，万有引力定律公式，牛顿第二定律真的非常简单而又准确地描述了客观世界的运动，因此才有“天不生牛顿，万古如长夜“之说，而且这个说法是世人公认的，绝无异议，无论多么守旧的人都无法否认。现在我们看如何描述一个椭圆：要描述一个椭圆，至少需要二个参数，现在大家都知道椭圆中心在坐标原点，长轴在
现在我们转换一个角度，现实生活中，我们描述任何一个物体，一定要有一个描述他的参考系统。假如我们要描述一个名字叫张三，土生土长的广东人，描述他的参考系统是30个长得完全互相不相像的土生土长的东北人，于是我们要从这30个东北人中挑选一个鼻梁较短的
上面的例子有几个关键的东西：第一个是描述张三的参考系统，也就是全体东北人，第二个就是选择长得完全不想象的30个东北人，张三只需要和这30个人比较就可以了，第三个就是张三和某个东北人的局部身体特征的相似性计算问题。这三个问题搞明白了，也就搞清楚所有的线性变换的基本思想了。
第一个问题是参考系统，也就是所有参照物的集合，也就是所有元素的集合，对照这个例子就是所有东北人的集合，我们希望张三如果也是东北人最好了，也就是我们研究的目标是参照系统里面的一个分子，否则正如我们上面的例子，如果选用全体猫咪的集合来描述张三，那么就很困难了，甚至无法描述。因此我们研究一个目标时候，选择的参考系统也就是集合一定含有这个目标，这就是Banach空间，也就是完备的赋范线性空间。这个空间意味着任何一个元素列收敛于该空间。
第二问题就是典型的元素问题，也就是有代表性的元素确定问题。上面我们选择30个完全不相似的东北人来代表所有的东北人。为什么要这样呢？现在又涉及到一个简化问题，全体东北人太多了，我们不可能将张三和每一个东北人的鼻子进行相似性评判，我们只要和代表性的具有不同特征东北人进行比较即可，也就是简化集合里面的元素，这个也是可以理解的。一个集合里面可能有无数个元素，我们如果要尽量简单的表达这个集合，显然就希望选择代表性的元素，而集合中的其它任何元素都能够被这些具有代表性的元素表达出来，而这些元素组成的集合又是能表达所有元素的最小集合，于是很显然的得出了线性无关组的概念，也就是找到集合中的最大线性无关组，那么其它所有的元素都能够被这个线性无关组表达。具体到一个函数组成的空间，我们希望能够找到一组基函数，空间里所有函数能够被这组函数表达出来。我们没有具体讲线性空间，线性无关，线性相关等概念，这些概念不是我们要讲述的，任何一本线性代数教材都可以查找到。
第三个问题就是元素的相似性计算问题。也就是我们采用什么手段来评判张三的鼻子和某一个东北人的鼻子相似程度，我们总不能靠感觉说像还是不像，要给出数学公式，这就是空间的内积定义，也就是定义内积的Banach空间，即希尔伯特空间了。从希尔伯特空间的角度上说，任何两个元素进行内积运算，就是比较这两个元素的相似程度。至于内积到底是什么，泛函分析给出一般定义，用户只要寻找一个具体的运算方式满足这个一般的定义就可以了。
我们谈到了上面的三个问题，涉及到完备的线性空间，即Banach空间，元素的线性表达，定义了内积的希尔伯特空间，这就是泛函分析的基本内容。本来这种简单而精确的表达思想就是针对Lebesgue空间的可测函数的表达问题，结果一抽象，抽象到张三的描述问题，完全脱离了函数问题，变成了针对希尔伯特空间的抽象元素的表达，不论什么集合，只要元素中定义了范数，定义了内积，具有完备性，就是希尔伯特空间，是希尔伯特空间就可以对任何一个元素进行描述了。上面讲了几个概念，读者查查就可以了解到底是什么，不要说这里讲难了，数学是哲学，总要给出一些定义和概念，否则说不清楚，关键是读者别将这些概念神秘化就可以了。
那么我们回到出发点，首先看看傅里叶变换搞得是什么东西，就从前面我们谈到的三个问题入手进行讨论。为了简化，我们假如所有的在区间
从上面的公式，我们看出两个向量的相似度就是它们对应坐标的乘积，也就是内积是它们对应坐标的乘积。那么现在我们如何根据这种思想计算
我们将区间
这样一来我们得出两个基本结论，第一个结论就是只要在空间
我们再回归到傅里叶变换，选定三角基函数，傅里叶变换后获得的
如果没有希尔伯特空间的概念，就一下子难以理解函数重构了，但是想想欧氏空间是怎么写一个向量的？假如二维坐标系下一个向量为
估计很多人都知道傅里叶变换高阶矩表示一个函数曲线的整体形状，低阶矩表示函数中的细节部分，这表明大多数函数和低频率的余弦函数相似，因此人们常常使用这些低阶矩重构函数，因此函数曲线中一些局部细小的起伏就会过滤掉，这也是一种信号平滑手段。我们考查下面函数
这个函数曲线类似一个矩形，在使用傅里叶变换重构该函数时，假如使用前10个矩可以较好的逼近函数的直线部分，但是在
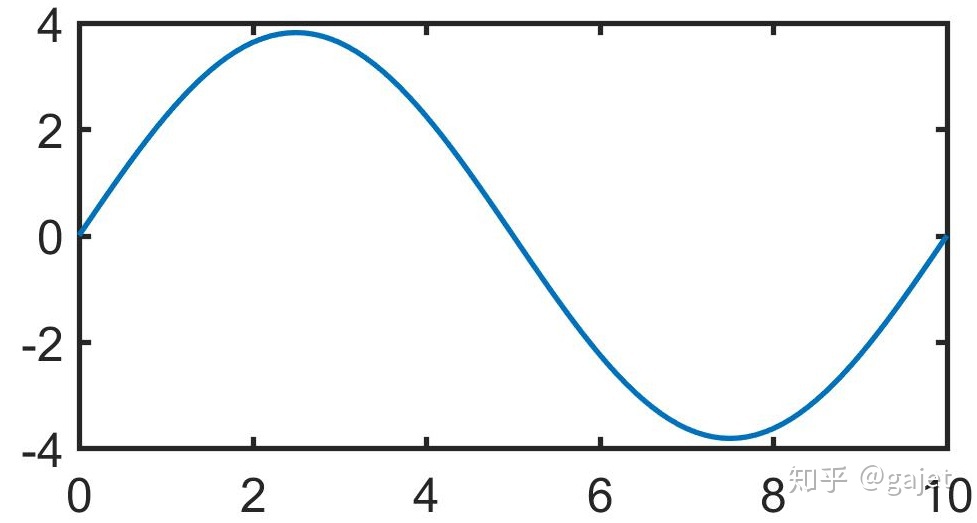
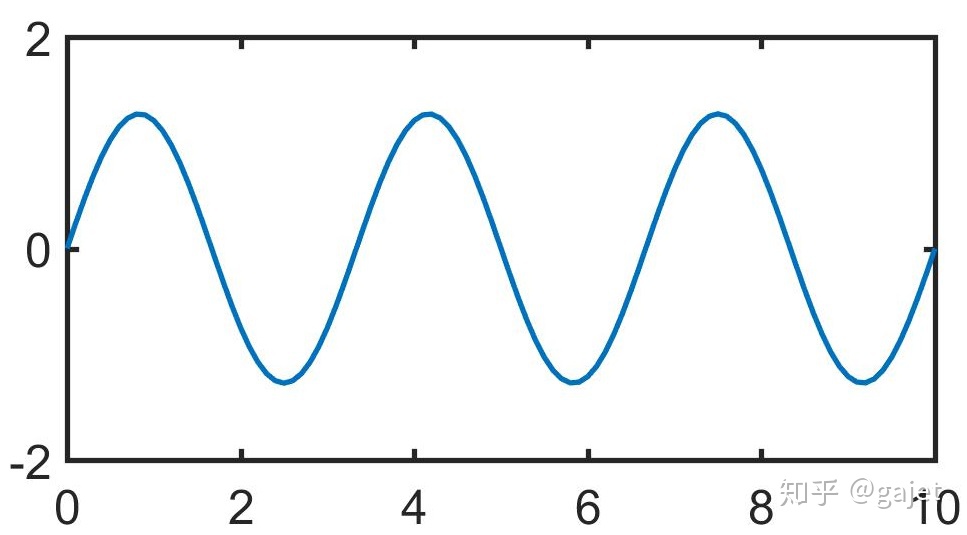
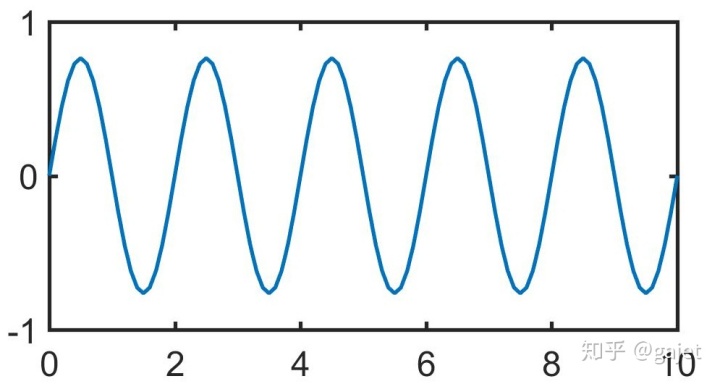
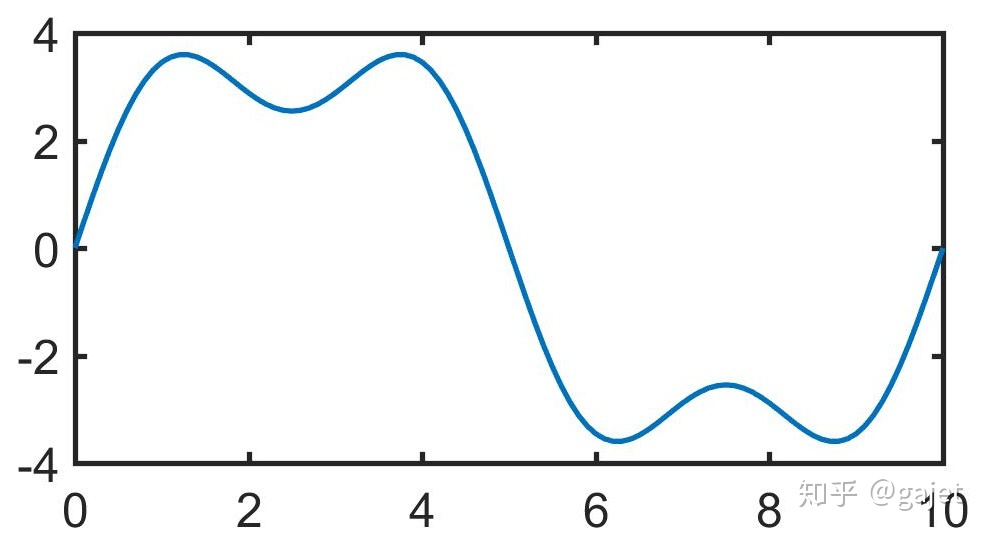
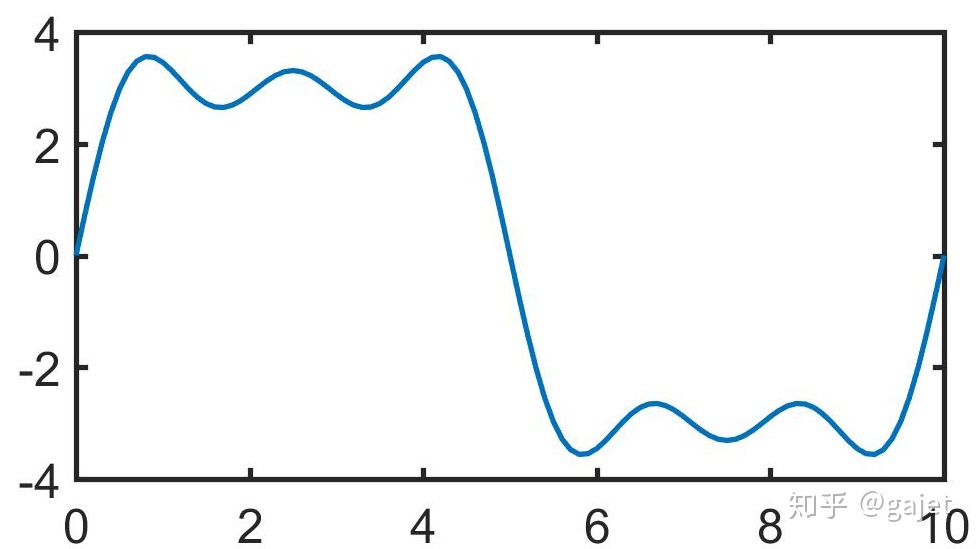
观察上面图2，图3和图5，很容易发现在横坐标为5的时候第一个波形和第二个波形恰好在这个位置具有相同的下降趋势，因此这两个波形相加，体现在图5就是在横坐标为5的领域范围内，生成了一个较长的斜线，再加上第四个波形生成图6，会发现在此位置，斜线进一步变得陡峭，而分析横坐标为2，4等领域范围，会发现它是如何逐渐变成直线的，也能理解它如何不停的围绕该直线进行上下波动的。特别注意图3和图4，它们的振幅越来越小，也就是傅里叶变换的数值越来越小，频率越来越高，正是这个特点才使得每次三角函数项累加以后，就小幅度修正，进而逼近该函数曲线。
现在我们换一个角度讨论，傅里叶变换可以看作一个函数在基函数上的投影大小，于是我们将这种投影运算记作
还是没有说清楚线性变换的特征值和特征向量的关系。现在我们进一步讨论，上面我们讲任何一个元素经过一组基元素变换后就可以重构该元素，这里面就涉及到泛函分析里面的一个投影算子，即一个元素和基元素的内积再乘以该基元素，也就是和基元素的相似性在乘以基该元素可以看作一个算子，就是投影算子，那么任意一个元素，如果是投影空间的一个元素，那么该元素在空间的投影就是本身，故函数空间各种变换实质上就是基函数的线性表达。这就是该元素在各个基所组成空间的投影和。这时的基就是特征向量，投影的值就是特征值。现在我们看一般线性变换的特征值和特征向量，假设线性变换
现在变换后的坐标是
连续空间的正交基函数有无穷多，比如 Hermit正交多项式，Chebyshev正交多项式，Laguerre正交多项式，Legendre正交多项式，都可以作为连续函数空间中的正交基函数，于是对于任何一个给定函数，都可以计算和各个基函数的内积，进而使用基函数的线性组合表达该函数，于是就有Hermit变换，Chebyshev变换，Laguerre变换，Legendre变换，当然还有其它非多项式基函数，比如小波变换等等。这些变换可能有无数个，反正找一组正交基，就对应一个变换，类似于平面直角坐标系，旋转一个角度，在平面上的一个点就对应在这个坐标系下的一个新坐标，比如 一个点的坐标为
现在我们回到希尔伯特空间， 对于任何希尔伯特空间的一个元素，如果要稀疏表达，无怪乎从两个方向研究，一个是寻找一组固定的基元素组，它们能够稀疏的表达任何元素，另外一个研究方向是针对该元素自适应的选择基函数以达到稀疏表达的目的。显然第一个是最理想的，问题是目前提出很多变换，还没有发现一个变换能够达到该要求，于是从第二个方向进行研究，但是这也是极其困难的，原因是希尔伯特空间中的元素特点很难完全认识清楚，如果完全认识清楚，也不需要选择基函数来表达了，这就陷入了一个矛盾状态中，现在我们简单的进入下面关于图像分析的讨论。
图像处理的研究基本上是对图像的像素点矩阵数据进行处理，一个像素点对应一个灰度值，一幅图像就对应一个二维数值矩阵，现在要使用二元函数表达它，目的是能够对它进行稀疏表达，从而为数据压缩，噪声去除，边缘检测，目标分割，物体识别等服务。但是图像内容实在太丰富了，有复杂的纹理，有简洁的线条，有光滑的曲线，有凌乱的噪声。我们回顾上面的例子，就是一个简单的方形函数，使用傅里叶基变换都无法高效描述它，而这仅仅是一维空间的讨论，现在我们基本明白对于一个方形函数使用傅里叶变换难以表达的原因就是使用曲线去逼近一条直线当然困难了，怎么可能效率高呢？可能有的人就会说，为什么不用直线描述呢？这当然可以，问题是现实客观世界的情况是：获得的实际数据信号图形一部分是直线，一部分是曲线，有的是夹杂各种不同斜率的直线和各种复杂的函数曲线，这时候很难找到一个有明确的解析式而且类似多项式的函数充当基函数来表达它们。这其实是矛盾的，想想看，哪个连续函数的图形能够随随便便的从直线光滑的过渡到曲线，而且在直线和曲线上随意转换，并且还是一组函数并满足正交性？于是又有人提出，能不能寻找这样的函数，它是分段函数，在一个区间上是某一个解析函数，在其它区间是0，这样局部描述，直线部分使用直线，曲线部分使用曲线，这样效率就来了，还真有人这么做了，而且很出名，这就是小波变换。我们现在提到小波变换，可以高效描述一维数据，那么对于二维图像数据怎么办？人们马上想到，这个如同傅里叶变换一样，扩展到两维，也就是使用张量积的形式进行推广，这样一推广，人们发现小波分析存在巨大问题，也就是二维图像中的水平直线，垂直直线和45度角的斜线，小波变换可以很好的表达这三种类型的直线，其它类型的直线和曲线无法有效表达，但是一幅图像怎么可能只有这三种直线？实际图像中各种倾斜的直线都有，更可能的是曲线，比如一个老人面目的皱纹，那是弯弯曲曲的从额头一直延续到下巴，总不能要求老人的皱纹要么长的水平，要么长得垂直，以方便科研开发人员搞小波变换处理？这样一来的确困难了，但是虽然困难，那也得想办法啊，只要想出办法，科研人员就可以发论文，评职称，拿项目，还可以成为什么什么高端人才。开发人员就可以弄出各种产品来推向市场，其实开发人员估计经常骂科研人员，写的文章，说算法怎么怎么改进了，其实只是针对某一类特殊图像才适用，根本不通用，还有就是假的，编造的，效果还不如我们使用传统的方法好呢？不管怎么说，有人提出了针对小波分析的改进措施，进而将小波分析推进到后小波分析时代，这就是多尺度几何分析。这些方法具体包括脊波(Ridgelet)变换，曲波(Curvelet)变换，轮廓波(Contourlet)变换，条带波(Bandelet)变换，楔波(Wedgelet)变换，小线(Beamlet)变换等等。本文作者对有的有些变换没有完全搞懂，但是大体了解其思想，了解以后感觉到有些无趣，为什么这么说呢？我们还是结合其它作者的理解谈谈这些分析，然后再说怎样的无聊。
(1)Ridgelet变换：属于非自适应变换。小波变换不是无法稀疏表达任意方向的直线吗，但是它能高效的表达点，那么怎样才能将图像中的直线变换成一个点呢？估计学过图像处理的都知道，Randon变换，或者Hough变换，这两个变换能把图像中任意方向的直线变换成一个点，这样一来就可以用小波变换进行表达了，这就是Ridgelet变换，是不是有点无趣？但是图像中的边缘线条很多是曲线，对整幅图像进行Ridgelet分析一定不理想啊！于是又有人提出了单尺度脊波(MonoscaleRidgelet)变换，具体方法是对图像进行分块，使每个分块中的线条都近似直线，再对每个分块进行Ridgelet变换，这就是多尺度Ridgelet，这个就更无趣了。
(2)Curvelet变换：第一代Curvelet变换是所有可能的尺度上进行分解，然后在每一个尺度使Ridgelet变换，不像Ridgelet变换那样是固定的：具体步骤是先对图像进行子带分解；然后对不同尺度的子带图像采用不同大小的分块；最后对每个分块进行Ridgelet分析。如同微积分的定义一样，在足够小的尺度下，曲线可以被看作为直线，曲线奇异性就可以由直线奇异性来表示，这个方法也许的确能改进图像的表达，但是在理论上很无聊了。
(3) Contourlet变换。Contourlet变换将多尺度分析和方向分析分拆进行，首先由LP(Laplacian pyramid)变换对图像进行多尺度分解以“捕获”点奇异，接着由方向滤波器组(Directional Filter Bank, DFB)将分布在同方向上的奇异点合成为一个系数。Contourlet变换的最终结果是用类似于轮廓段(Contour segment)的基结构来逼近原图像，这也是所以称之为Contourlet变换的原因。这种变换感觉缺乏传统基函数表达的那种美感，感到无趣。
(4)Bandelet变换。Bandelet变换的思想是定义图像中的几何特征为矢量场，矢量场表示了图像空间结构的灰度值变化的局部正则方向。Bandelet基并不是预先确定的，而是以优化最终的应用结果来自适应地选择具体的基的组成。这个是自适应基函数表达方法，但是要自适应寻找基函数，而且又是需要分块，也是感觉不好。
(5)Wedgelet变换。该变换就是在一个图像子块(dyadic square)画条线段，把它分成两个楔块，每一个楔块用唯一的灰度值表示，线的位置就位于两个楔块之间，这种方法做的更狠，什么基函数不基函数的，直接上优化方法，将分块一切两半，如果这个分块真的有直线段，那么直线段两边的灰度值一定不同，因此它们的均值相差就很大，于是做优化处理，也就是随便划一条直线段，两边楔块的灰度值大的直线就是图像边缘，其实这种方法本质上是积分的方法，有点意思，但是没有什么数学理论做支撑，更没有什么意思了。
(6)Beamlet变换。该变换以各种方向、尺度和位置的小线段为基本单元来建立小线库，图像与库中的小线段积分产生小线变换系数，以小线金字塔方式组织变换系数，再通过图的形式从金字塔中提取小线变换系数，从而实现多尺度分析。这是一种能较好进行二维或更高维奇异性分析的工具。根据小线理论及其研究结果来看，它对于处理强噪背景的图像有无可比拟的优势。但是小线变换的前期准备工作，如小线字典、小线金字塔扫描这些部分的工作量太过于庞大，不利于研究。如果能将这部分简化，或者做成固定的模块引用的话，小线分析能够很快的扩展其应用领域。
看来Beamlet变换和Wedgelet变换都是一种积分方法，大家都知道对付噪声，积分方法是根本的考虑，其实积分方法的弊端就是将边缘也当成噪声，如何保留边缘而又能去除噪声，这和图像的稀疏基函数表达要求是一致的，我们看上面提到的方形函数，如果直线段上有噪声，那么直线段含有高频信号，但是在直线段边缘明显的发生了跳跃，这部分信号频率更高，但是它却是这个函数曲线最关键的特征，如果将它作为噪声过滤掉，那么这个方形图形就成了一个有圆角的梯形，这下子事情就闹大了。那么如何保留方形直角特征又能去掉噪声呢？如果直线用直线逼近，边缘曲线用边缘曲线逼近就好了，可是我怎么知道那些是曲线，哪些是直线，那些事拐角？上面所谓的多尺度几何分析方法就是本着两个思路去的，第一个是检测啊，找出这些特征的边缘，第二个就是优化啊，固定一些模板，进行优化比较。第一种方法是既丑又不好用，第二种方法也许好用，但是丑。
那么怎么办呢？。。。。。。想想啊，其实想出一个通用方法，可能是调和分析的一个新的研究方向。真是奇怪，对于线性变换，我们能够找到特征向量作为一组基，然后用这组基很简洁的表达这个线性变换，但是对于一个元素，我们却很难找到一组基来简洁的表达它，奇怪！
最后一点说明，我们没有将傅里叶变换涉及到的连续谱等概念进行讨论，也没有提到谱分析，因为这个可能太花时间，另外一个重要的原因是本文作者感到自己仍然需要深入理解它。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
