取出整数的每一位数_长整数的乘法运算

因为头条不支持 markdown 中使用公式表示, 所以下面涉及公式的地方, 我使用截图替换了下.

概述

都知道, 计算机中存储整数是存在着位数限制的, 所以如果需要计算100位的数字相乘, 因为编程本身是不支持存储这么大数字的, 所以就需要自己实现, 当然了, 各个编程语言都有大数的工具包, 何必重复造轮子, 但我还是忍不住好奇他们是如何实现的, 虽然最终没有翻到他们的底层源码去, 但查询的路上还是让我大吃一惊, 来吧, 跟我一起颠覆你的小学数学.

长乘运算

当然, 如果自己实现这样一个大数, 用数组来存储每一位是我当前想到的方法. 那如何进行乘法运算呢? 因为用数组来存储数字, 那么数字的加法也要采用每一位进位的方式来进行, 所以下面为了方便说明算法的效率, 以一次个位数的运算视为一个运算单位.

上小学知识:

通过上面可总结规律, n位数乘一位数, 需要 2n 次运算. 将 n 位数乘1位数的运算称作短乘. 然后下面再看一下 n 位数乘 n 位数.

通过上面, 总结规律, n位数相乘(长乘)的运算次数是: ​ 次运算. 当然, 这就是我们从小接受的进行乘法运算的方法, 所以写成这样还好, 比较合乎常理. 时间复杂度是 O(n^2)

但是, 他还可以更快么? 我以为就这样了, 是我小看了伟大的数学家. .

Karatsuba方法

由简入难, 先看一下两位数的乘法:

12*34, 为了方便初中方程未知数的思维, 我们将这两个数字拆解一下:

其中其中

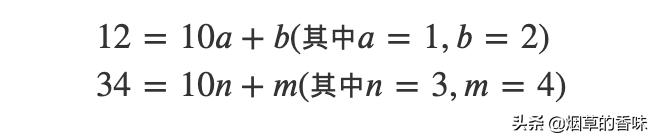
则,

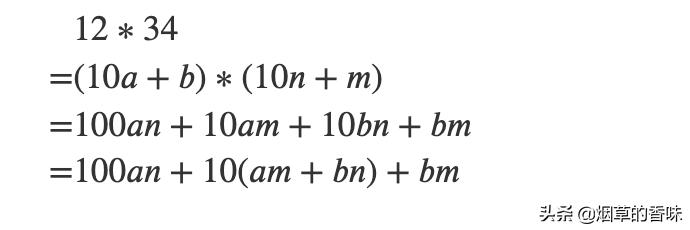
当化简到这里, 2位数相乘需要几次运算? 来算一下:

此时, 需要的运算次数已经较之前的12次少一些了, 但是别急, 容我把公式再变换一下.

令:

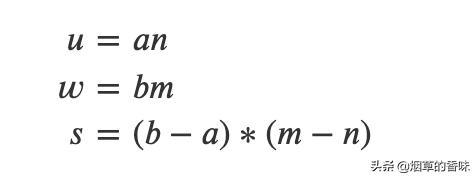
公式:

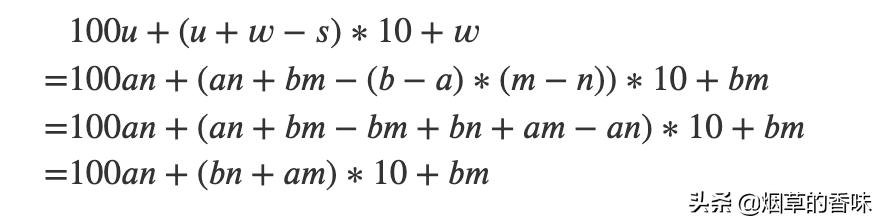
是不是和上面的公式一样了呢? 是的, 那转换公式是为了什么呢? 当然是为了减少运算次数啦. 算一下:

• 计算u : 1次运算
• 计算w: 1次运算
• 计算 s: 3次运算
• 计算 u+w-s: 2位数运算, 2次运算
• 计算最外层加法: 3位数运算, 3次运算
• 共: 10次运算.

这和我刚才计算的不也是10次么? 不过个位数的乘法换成加法就会变快了么? 不要小看这个一次乘法运算的减少, 从上面能够看出, 乘法运算的运算次数是随位数成指数增长的, 而加法运算则随位数成线性增长, 等看了下面的多位数相乘, 你就知道减少的这一次乘法运算有什么用了.

不过下面才是重头戏, 数字多了之后, 此算法就明显比传统的快的多了.

4位数乘法

计算: ​1234*5678

设:

套用上面的公式:

令:

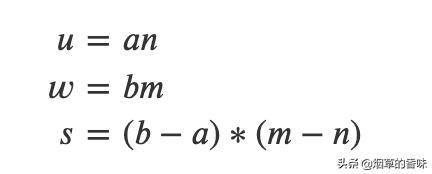
则结果为: ​

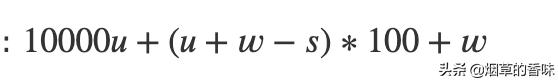
此次进行了几次运算呢? 算一下:

32次运算, 之前长乘的方式需要几次呢? ​. 是不是少了.

也就是说, 4位数的乘法, 其中用到了3次两位数乘法, 2次两位数减法, 1次8位数加法.

8位数乘法

8位数乘法就不展开了, 直接套用4位数乘法得出的结论, 其运算次数为:

原来的长乘需要几次呢? ​2∗(8∗8)+2∗8=144次.

是不是有一种动态规划, 分而治之的感觉? 可以利用函数递归来实现.

问题

想必此算法的问题也很明显了, 为了每次都能将数字拆成左右两部分, 所以只能够计算位数是2的 n 次方的数字, 如果位数不足, 则需要在前边进行补0.

算法比较

为了比较两个算法的运算次数, 让我们忽略运算的低次幂以及常数项, 则(以下 n 为2的幂):

长乘

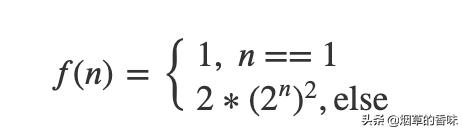
Karatsuba:

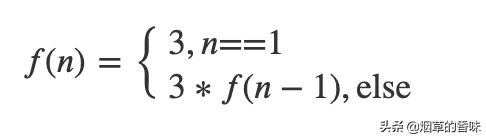
分别进行计算:

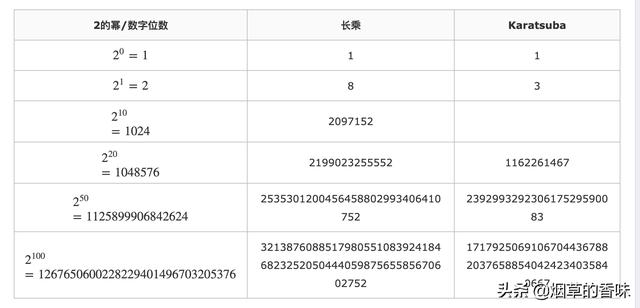
可以看出来, 当数字的位数越大, 则两个算法之间的差距越明显.

---

有没有被颠覆的感觉? 是不是自己知道了20多年的乘法运算, 根本没有想到还有其他计算乘法的运算规则? 我也没想到, 涨见识了...

果然, 没有什么是伟大的科学家们做不到的, 这算法我看了近乎整整一天, 草稿纸废了四十张, 总算是略知一二了.