
新智元报道
来源:arXiv
编辑:三石、肖琴
【新智元导读】ImageNet 训练纪录再次被刷新!富士通实验室在 74.7 秒内完成了 ImageNet 上训练 ResNet-50 网络,使用 2048 个 GPU,准确率为 75.08%,刷新了此前谷歌 1.8 分钟的记录。
在过去两年中,深度学习的速度加速了 30 倍。但是人们还是对 “快速执行机器学习算法” 有着强烈的需求。
Large mini-batch 分布式深度学习是满足需求的关键技术。但是由于难以在不影响准确性的情况下在大型集群上实现高可扩展性,因此具有较大的挑战难度。
最近,富士通实验室的一项研究刷新了一项纪录:

论文地址:
https://arxiv.org/pdf/1903.12650.pdf
这项研究在 74.7 秒内完成了 ImageNet 上训练 ResNet-50 网络,使用 2048 个 GPU,准确率为 75.08%,刷新了此前谷歌 1.8 分钟的记录。

表1:ImageNet上训练ResNet-50的记录
增加 mini-batch 大小,实现短时间内的高准确性基于大数据集的深度神经网络 (DNN) 模型在对象检测、语言翻译等领域取得了令人瞩目的成果。然而,随着 DNN 模型和数据集规模的增大,DNN 训练的计算量也随之加剧。
具有数据并行性的分布式深度学习是加速集群训练的一种有效方法。
在这种方法中,集群上启动的所有进程都具有相同的 DNN 模型和权重。每个过程都用不同的 mini-batch 训练模型,但是来自所有过程的权重梯度被组合以更新所有权重。
对于大型集群,这种通信开销成为一个重要的问题。
为了减少大型集群的开销,该研究增加了 DNN 的 mini-batch 大小,且并行计算了 DNN 训练。然而,在 minni-batch 训练中,DNN 模型的验证精度普遍较差。
因此,研究者们采用了几种技术来增加 mini-batch 的大小,这表明了在迭代中计算的输入图像的数量,而不会影响验证的准确性。
在实验过程中,本文使用了人工智能桥接云基础设备 (AI Bridging Cloud Infrastructure,ABCI) 集群 GPU 和 自优化的 MXNet 深度学习框架。并在 ImageNet 上使用 81,920 mini-batch 大小,74.7 秒内实现了 ResNet-50 的 75.08%验证准确度。
技术方法三部曲本文的技术方法主要分为三个部分:准确性改良、框架优化和通信优化。
A. 准确性改良
这部分采用了通常用于深度学习优化器的随机梯度下降(SGD)。在对 large mini-batch 进行训练时,SGD 更新的数量随着小型批大小的增加而减少,因此提高 large mini-batch 的最终验证精度是一个很大的挑战,本文采用了以下技术。
学习速率控制:由于更新数量较少,需要使用高学习率来加速训练。 然而,高学习率使得模型训练在早期阶段不稳定。 因此,我们通过使用逐渐提高学习率的预热 (warmup) 来稳定 SGD。 此外,对于某些层,所有层的学习速率都太高了,还通过使用层次自适应速率缩放(LARS)来稳定训练,LARS 根据规范权重和梯度调整每层的学习速率。
其它技术:据报道,标签平滑提高了 32,768 个 mini-batch 的准确性。本文也采用了这种方法,并对 81920 个 mini-batch 进行了精度改进。
batch 标准化层的均值和方差的移动平均 (moving average) 在每个过程中独立计算,而权重是同步的。这些值在 large mini-batch 上变得不准确;因此,本文调整了一些超参数来优化移动平均线。
B. 框架优化
我们使用了 MXNet,MXNet 具有灵活性和可扩展性,能够在集群上高效地训练模型。然而,在中小型集群环境中只占总时间的一小部分的处理方式可能成为大规模集群环境中的瓶颈。我们使用了几个分析器来分析 CPU 和 GPU 性能,找出了瓶颈。我们对瓶颈进行了优化,提高了训练吞吐量。
1) 并行 DNN 模型初始化:
在数据并行分布式深度学习中,必须初始化所有层,使所有进程的权重相同。通常,根进程初始化模型的所有权重。然后,进程将这些权重传递 (broadcast) 给所有进程。传递时间随着进程数量的增加而增加,在有成千上万个进程进行分布式深度学习时,其成本不可忽视。
因此,我们采用了其他初始化方法,即每个进程具有相同的种子并并行地初始化权重。这种方法无需 broadcast 操作就可以同步初始权重。
2) GPU 上的 Batch Norm 计算:
每层的 norm 计算都需要使用 LARS 更新权重。与 GPU 上的内核数量相比,ResNet-50 的大多数层没有足够的权重。如果我们在 GPU 上计算每一层的 weight norm,线程数不足以占据所有 CUDA 核心。因此,我们实现了一个特殊的 GPU 内核,用于 batched norm 计算到 MXNet。该 GPU 内核可以启动足够数量的线程,并且可以并行计算层的范数。
C. 通信优化
分布式并行深度学习要求所有 reduce 通信在所有进程之间交换每一层的梯度。在大集群环境中,由于每个 GPU 的 batch size 较小,使得通信时间变长,计算时间变短,因此 reduce communication 开销是不可忽略的。为了克服这些问题,我们采用了以下两种优化方法。
1) 调整通信的数据大小
2) 通信的优化调度
实验设置与实验结果我们使用 ABCI 集群来评估基于 MXNet 的优化框架的性能。ABCI 集群的每个节点由两个 Xeon Gold 6148 CPU 和四个 NVIDIA Tesla V100 SXM2 GPU 组成。此外,节点上的 GPU 由 NVLink 连接,节点也有两个 InfiniBand 网络接口卡。图 1 为 ABCI 集群节点结构示意图。
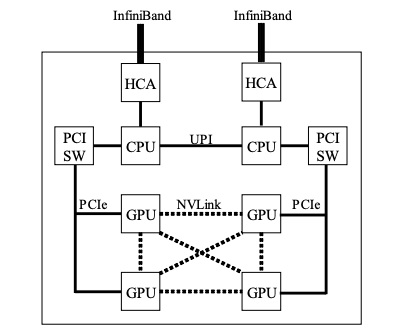
图 1:ABCI 集群中一个计算节点的示意图。它由两个 GPU、四个 GPU 和两个连接到相应 CPU 的 HCA 组成。
我们使用混合精度方法,使用半精度浮点数计算和通信,并使用单精度浮点数更新权重。我们使用了原始优化器,它可以很好地控制学习率。除了稳定训练精度外,我们还使用了 warmup 和 LARS 技术。
我们对 ResNet-50 训练的测量依据 MLPerf v0.5.0 规则。也就是说,我们度量了从 “run start” 到 “run final” 的运行时间,其中包括初始化和内存分配时间。
结果表明,优化后的 DNN 框架在 74.7 秒内完成了 ImageNet 上 ResNet-50 的训练,验证精度为 75.08%。
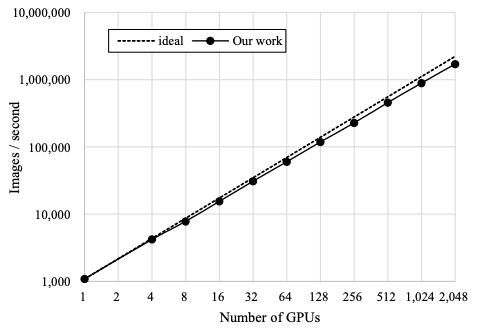
图 2:优化后的框架的可扩展性用实线表示,虚线表示理想曲线。
我们还测量了 ResNet-50 的可扩展性。图 2 显示了根据 GPU 数量计算的吞吐量。在图 2 中,虚线表示理想的每秒图像吞吐量,实线表示我们的结果。如图表明,直到 2048 个 GPU,我们的框架的可扩展性都非常好。使用 2048 个 GPU 的吞吐量为每秒 170 万张图像,可扩展性为 77.0%。
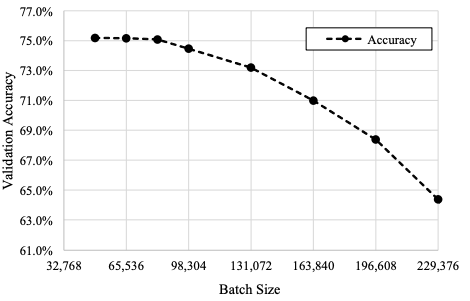
图 3:在 49152 个或更大的 mini-batch 训练中,top-1 验证精度的变化
图 3 显示了 81,920 个或更大的 mini-batch 训练中 top-1 验证精度的结果。从图 3 中可以看出, mini-batches 超过 81,920 个的验证精度低于 74.9%,不符合 MLPerf 规定。因此,ImageNet 数据集一个 epoch 的图像数量为 1,280,000 张,如果使用 81,920 mini-batch,一个 epoch 中的更新数量仅为 16 张,其中更新总数为 1,440 张。这个数字太小,SGD 求解器无法训练 DNN 权重。因此,使用大的 mini-batch 是一个很大的挑战,我们尝试使用尽可能大的 mini-batch。
如表 1 所示,与其他工作相比,81,920 mini-batch size 已经很大,验证精度达到 75% 以上。
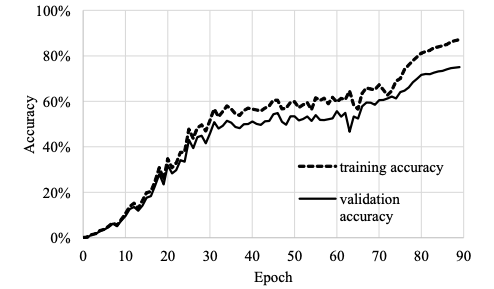
图 4:训练精度与验证精度之比较
图 4 显示了训练精度与验证精度的对比。从图中可以看出,使用 batch normalization 和 label smoothing 技术,我们的验证精度结果并没有过拟合。
结论我们开发了一种新的技术,可以在大规模 GPU 集群上使用 large mini-batch,而不会降低验证精度。我们将该技术应用到基于 MXNet 的深度学习框架中。使用 81920 minibatch size,我们的 DNN 训练结果在 74.7 秒内训练完 ResNet-50,验证精度达到 75.08%。
论文链接:
https://arxiv.org/pdf/1903.12650.pdf
更多阅读
大学统计学白上了?800多科学家联名反对“统计学意义”,P值该废了
中国籍博士一作登Nature封面:仿生群体机器人问世,工程学重大突破!
【2019新智元 AI 技术峰会精彩回顾】
2019年3月27日,新智元再汇AI之力,在北京泰富酒店举办AI开年盛典——2019新智元AI技术峰会。峰会以“智能云•芯世界“为主题,聚焦智能云和AI芯片的发展,重塑未来AI世界格局。
同时,新智元在峰会现场权威发布若干AI白皮书,聚焦产业链的创新活跃,评述AI独角兽影响力,助力中国在世界级的AI竞争中实现超越。
嘉宾精彩演讲:
腾讯云副总裁王龙:《解决AI技术落地难题,“解耦”是关键》
华为消费者业务首席战略官邵洋:《P30为什么这么贵还卖的火?除了麒麟芯片,背后还有“飞轮”》
驭势科技创始人兼CEO吴甘沙:《无人车驶出寒冬?》





















 798
798











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








