直角三角形的边角关系_关于特殊三角形边角关系的总结

~~~~~~~分--隔--符~~~~~~~

《关于特殊三角形边角关系的总结》是我当年在中学学习的时候自己总结的，现在成了教育人的一份子。上个月花时间重新总结了一下，想着可以发表分享给更多的同仁。遂投稿给了几家杂志社，无奈，版面费用高昂，无力承担。

就只能发表在自己这个免费的公众号里，希望可以分享给更多的同仁，共同探讨学习。

三角形既是平面几何的基础，也是几何学习的重点。我们从小学开始接触学习三角形，到现在已经积累了不少关于三角形的知识。为了更好地掌握，需要我们对这些知识进行总结，找到其中的一般性与特殊性，有利于以后的学习。下面我就对特殊三角形进行了一点总结，希望可以和大家共同探讨学习。

对于一般三角形的边角关系主要有：①两边之和大于第三边，两边之差小于第三边；②三角形的内角和为180°；③三角形外角和为360°；④直角三角形的勾股定理等。

中学阶段常接触到的特殊三角形主要包含以下几种：30°直角三角形、45°直角三角形、3-4-5直角三角形、等边三角形、36°黄金三角形、108°黄金三角形、120°等腰三角形。虽然课标只要求了前四种，但是其他的几种情形在考试和平常练习中也经常出现，如果能熟悉这些特殊三角形的模型，那么在做题的时候就可以快人一步，抢先解出答案，节省解题时间。

一、30°直角三角形

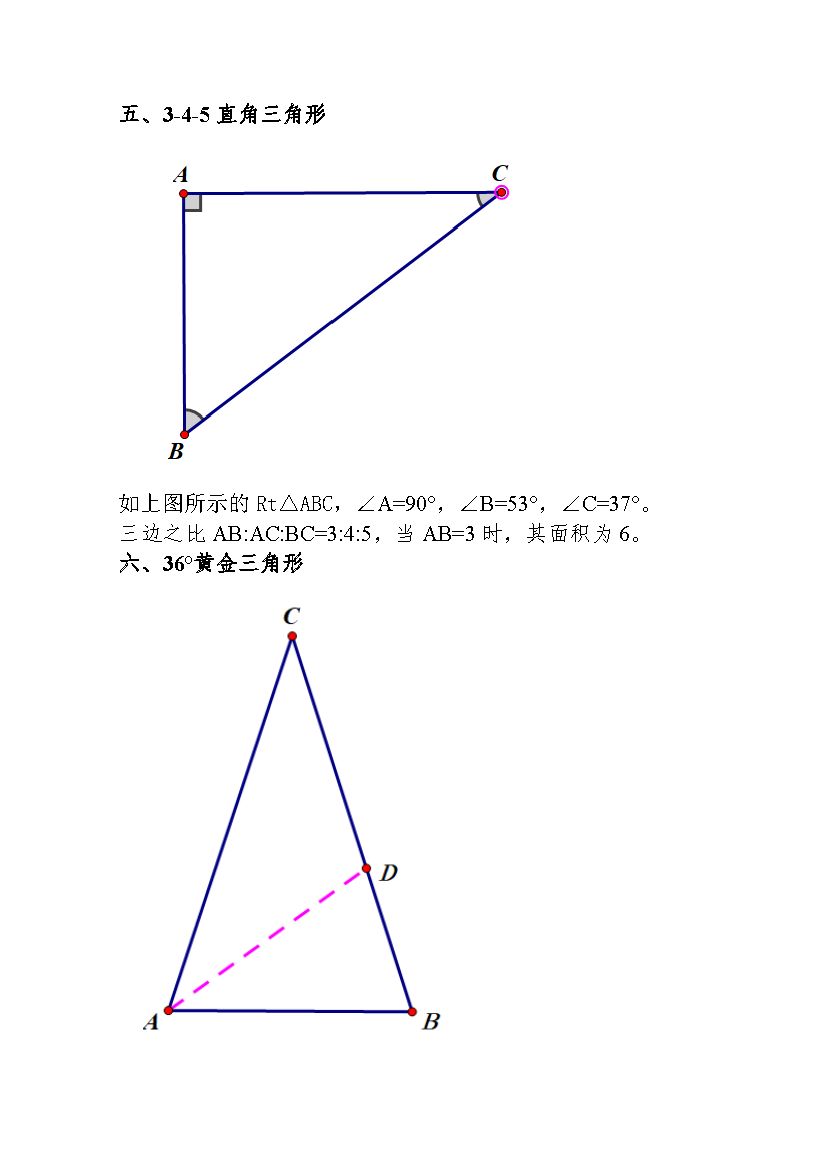
如上图所示的Rt△ABC，∠A=90°，∠B=60°，∠C=30°。

其三边之比AB:AC:BC=，此结论通过勾股定理可以很容易就给出证明。当AB=1时，其面积为，其他与之相似的三角形面积也是它的倍数。

二、45°直角三角形

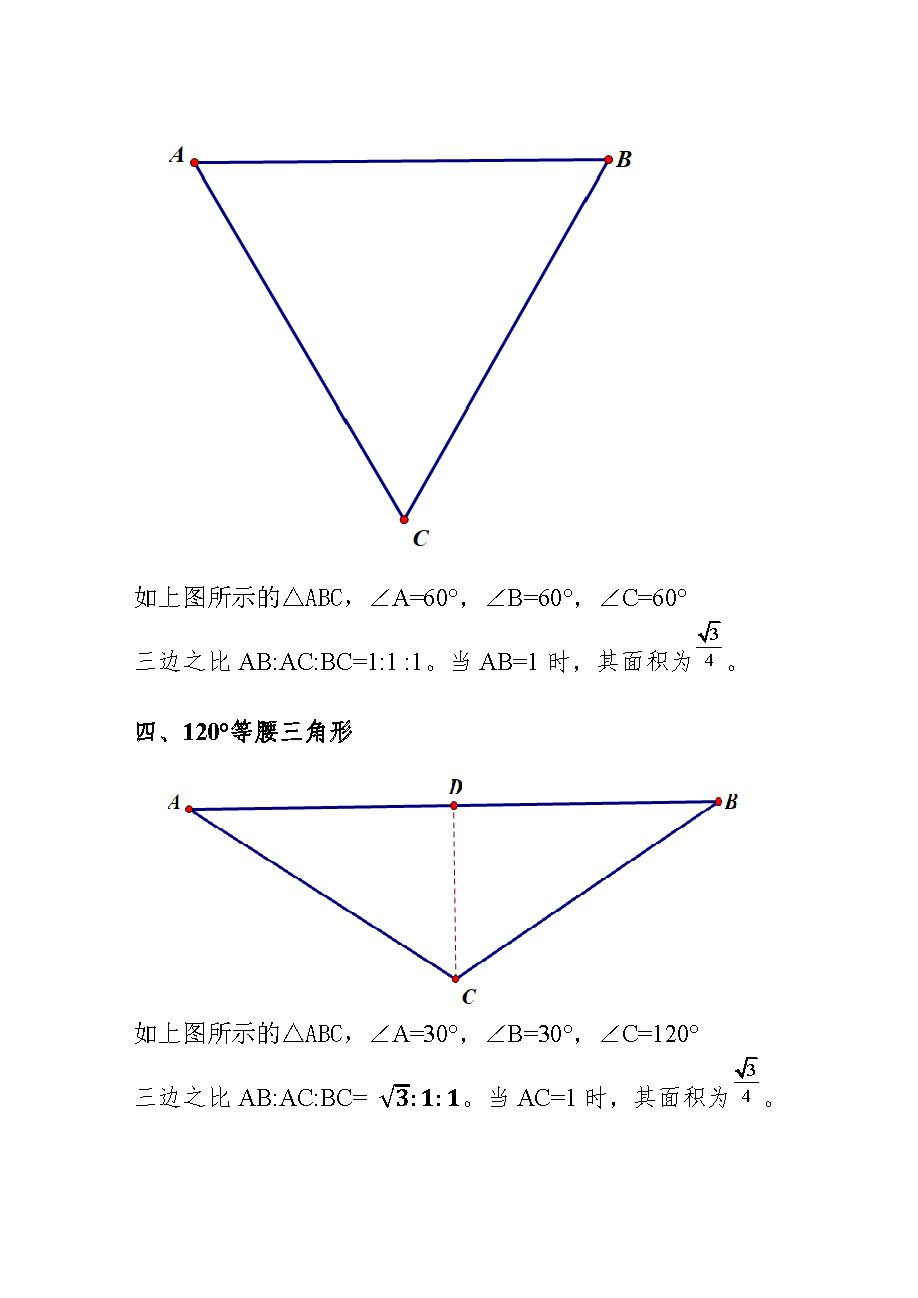
如上图所示的Rt△ABC，∠A=90°，∠B=45°，∠C=45°。

其三边之比AB:AC:BC=，此结论通过勾股定理也可以很容易就给出证明。当AB=1时，其面积为。

 …………………………………………

特殊三角形的边角关系结论不仅适用在几何计算，还用于解三角函数问题，特别是直角三角形，还有利于对三角函数值的理解和记忆。初中阶段的学习多以模仿和记忆为主，所以，如果能够记住并理解这些结论，就可以更加快捷地解答题目，还有利于以后的学习。

---

若有人有心支持，可以与我联系【1349524227@qq.com】，可以发word原稿。

学习是自己的事情，成绩也是自己的，未来也是自己的。

~~~~~~~福--利--线~~~~~~~

打开支付宝首页搜“ 551637526 ”即刻领到红包，最高99元！红包有效期3天，每天都可领！

后台回复 关键字 “红包”，即可查看使用详情。

~~~~~~~E--N--D~~~~~~~