二分归并排序算法_手撕算法之归并快速堆排序

常见的排序算法，之前手撕过冒泡、插入、选择和希尔。链接：第一篇排序算法文章。除了希尔的变体，上述几种算法在工程上的应用机会不多，主要原因是时间复杂度有点高。它们的意义更多是一种教学或思维体操的目的。

本篇的三个排序算法则在实际操作中有相对高频的出场。它们的共性是，平均时间渐进复杂度都是O(nlogn)，代码中都可能涉及递归的技巧。另外，和上一次的四个排序算法相同，基于简洁性，仍旧采用连续数组的物理结构存储数据。

---

merge_sort

def merge_sort(lst):
    n = len(lst)
    if n 2:
        return lst
    half = n//2
    left = lst[:half]
    right = lst[half:]
    return merge(merge_sort(left), merge_sort(right))

def merge(lst1, lst2):
    i, j, k = 0,0,0
    tmp = [0]*(len(lst1)+len(lst2))
    while i and j         if lst1[i] <= lst2[j]:
            tmp[k] = lst1[i]
            i += 1
        else:
            tmp[k] = lst2[j]
            j += 1
        k += 1
    while i         tmp[k] = lst1[i]
        k += 1; i += 1
    while j         tmp[k] = lst2[j]
        k += 1; j += 1
    return tmp
    

merge_sort中文译为归并排序，顾名思义，里边包含了合并和递归。

代码的基本思路就是分而治之，不停地二分，直到每一组的最后只剩一个元素。用递归的方法可以很好地实现，递归深度就是二分次数，也即logn。递归见底后，开始合并。合并过程不得不使用到额外的内存空间，所以必须申请一段n维数组。然后利用双指针，遍历完当前阶段分治后的两个子数组，按照从小到大的次序复制进新数组。以上描述有点像“先把书读薄，再读厚”。

易错的地方是，忘记设置递归出口，导致引发‘超出最大递归深度异常’。另外还需要注意的是，merge函数里，第一个参数代表left，第二个代表right。所以判断条件lst1[i]<=lst2[j]，最好别忘了=号。因为子数组left总在right前面，为了保证排序稳定性，若lst1[i]=lst2[j]的情况，优先lst1[i]。

可以优化的地方主要在merge函数。我见过有一个比较pythonic的写法，如下：

def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    while left:
        result.append(left.pop(0))
    while right:
        result.append(right.pop(0))
    return result

可以看到，相比我的第一段代码，上边这个省略了i,j,k三个临时变量。它充分利用了python list的天然的栈特性，不管是append(压栈)还是pop(弹栈)，都可以绕开索引下标，从而简化了代码。

还有一个更通用(c++和java)的优化办法，就是使用边界哨兵。在left和right的最后一位设置最大值，则一个循环就搞定。代码如下：

def merge(lst1, lst2):
    L1 = len(lst1); L2 = len(lst2)
    lst1_copy, lst2_copy, tmp = [0]*(L1+1), [0]*(L2+1), []
    lst1_copy[:L1] = lst1[:]
    lst2_copy[:L2] = lst2[:]
    lst1_copy[-1], lst2_copy[-1] = sys.maxsize, sys.maxsize
    for _ in range(L1 + L2):
        if lst1_copy[0] <= lst2_copy[0]:
            tmp.append(lst1_copy.pop(0))
        else:
            tmp.append(lst2_copy.pop(0))
    return tmp

这里需要事先import sys。sys.maxsize很实用，是调用系统最大整型常量。因为每个子数组的最后一位都是最大常量这个哨兵，因此当其中一个子数组遍历完(弹栈)全部有效数据后，触发哨兵，另一个子数组的剩余数据无缝衔接，继续复制到tmp。

以上三种代码对应的其实都是二路归并，还有更牛逼的多路归并，以后再写。

---

quick_sort

def quick_sort(lst, first, last):
    if first         midindex = partition(lst, first, last)
        quick_sort(lst, first, midindex-1)
        quick_sort(lst, midindex+1, last)
    return lst

def partition(lst, first, last):
    pivot = lst[last]
    i = first
    for j in range(first, last):
        if lst[j] <= pivot:
            lst[i], lst[j] = lst[j], lst[i]
            i += 1
    lst[i], lst[last] = lst[last], lst[i]
    return i
    

快速排序简称快排，是应用最广泛的排序算法。几乎大部分主流编程语言自带的排序函数的底层实现都依赖快排。

快排的平均时间复杂度也是O(nlogn)，比归并排序优越的地方在于，它是原地排序，它不需要额外申请很大的内存空间。如果说merge的特点是自底向上处理运算，则快排的规律是自顶向下。

代码的基本思路是依然是分而治之，不过不像merge_sort那样无脑地均分，而是有序地分割。这里的关键是partition函数，它的作用是随机选择数组中的一个值作为分界点pivot，然后将小于等于该值的放前边，大于该值的放后边。如此不停地递归，直到遇到出口‘子数组分无可分’，即停止。

容易出错的地方是，quick_sort函数里的两个递归quick_sort，它们的首尾指针参数。前一个的last形参传入的是midindex-1，后一个的first形参传入的是midindex+1。也就是说，空出来的midindex位置不参与后续递归排序，它的位置已经固定。另一个易错点是，分界槽pivot代表值，而不是数组索引下标。最后做交换时，参与交换的是lst[last]而不是pivot。

还需要注意的是，quick_sort借助三个参数完成排序功能，二三参数代表首尾指针。这样代码写起来会容易很多，而且直观。如果和其他排序算法一样，只提供lst一个参数，当然也能实现。

另外，partition函数中pivot的选取，将直接影响整个排序算法的性能，从而导致介于最坏时间复杂度O(n^2)和平均时间复杂度之间。要知道归并排序的最好、最坏和平均时间复杂度都是O(nlogn)。我在这里选择数组最后一位作为pivot，事实上可以选择数组位置区间内的任何一个点。理想的pivot位，就是能够均匀地分配前后两段子数组。比如选取第一位作为pivot：

def partition(lst, first, last):
    pivot = lst[first]
    i = first + 1
    j = i
    while j <= last:
        if lst[j] <= pivot:
            lst[j], lst[i] = lst[i], lst[j]
            i += 1
        j += 1
    lst[i-1], lst[first] = lst[first], lst[i-1]
    return i-1

由上可知，如果选择first的值作为pivot，最终交换和返回的位置都是i-1而不是i。

partition函数的本质是沿特定方向逐一比较交换数据，某种意义上讲，和冒泡排序类似。我还见过一种比较pythonic的方法，如下：

def partition(array, start, end):
    pivot = array[start]
    low = start + 1
    high = end
    while True:
        while low <= high and array[high] >= pivot:
            high = high - 1
        while low <= high and array[low] <= pivot:
            low = low + 1
        if low <= high:
            array[low], array[high] = array[high], array[low]
        else:
            break
    array[start], array[high] = array[high], array[start]
    return high            

这段代码比较有意思，它的思路是首尾双指针相遇，当有大数在前，小数在后时，交换。直至low>high。整体的逻辑类似简单的选择排序。

---

heap_sort

def heap_sort(lst):
    n = len(lst)
    if n <=1:
        return lst
    maxheap_build(lst)
    for i in range(n-1, 0, -1):
        lst[0], lst[i] = lst[i], lst[0]
        n -= 1
        maxheapify(lst, n, 0)
    return lst

def maxheap_build(lst):
    capacity = len(lst)
    for i in range(capacity//2-1, -1, -1):
        maxheapify(lst, capacity, i)

def maxheapify(lst, n, father):
    while True:
        maxindex = father
        left = maxindex * 2 + 1
        right = maxindex * 2 + 2
        if left and lst[father]             maxindex = left
        if right and lst[maxindex]             maxindex = right
        if maxindex == father:
            break
        lst[father], lst[maxindex] = lst[maxindex], lst[father]
        father = maxindex

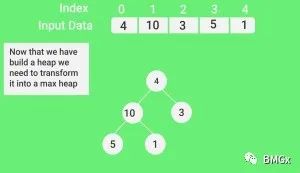
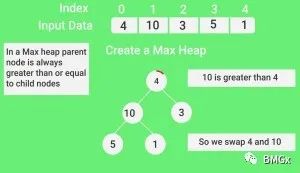
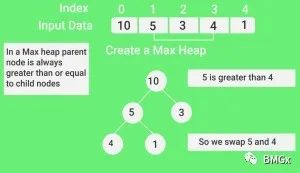
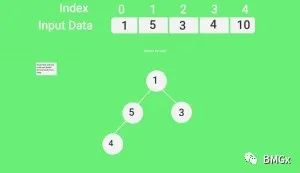
堆排序，和优先队列相关，它也使用了二叉堆这样的逻辑数据结构。二叉堆本质上是一种特殊的完全二叉树，其father值总大于或小于左右儿子值。总大于的叫大顶堆，总小于的叫小顶堆。而且完全二叉树特别适合数组存储结构，因此堆排序优先选择数组，代码形式也简单。

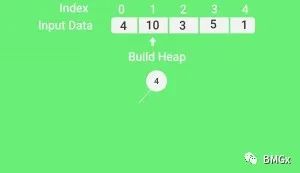
堆排序的整体思路是先构造堆，再排序。核心是堆化(heapify)函数。首先，构造堆(heapbuild)很有讲究，①可分为构造大顶堆，或小顶堆；②可分为自下而上构造，或自上而下构造。我上边的代码是自上而下地构造大顶堆，这种方式也是最普遍的。其次，排序的情况依赖构造方式，大顶堆就正排，小顶堆则逆排。

以我写代码为例，根据输入的待排数组先构造大顶堆。构造堆，实际上就是初始化一种堆结构。从数组的第  n//2-1位开始，从后往前(数组视角)，同时也是自上而下(二叉堆视角)地堆化maxheapify现有的完全二叉树。这是一个循环过程，直到把数组第一位(二叉树根节点)堆化完毕。

初始化结束后，根节点(堆顶)存储的是最大值，把它和最后一个叶子节点(数组最后一位)的值置换，完成第一轮正向排序。这么做(交换)是为了原地排序，而不用申请额外内存空间。

完成堆顶交换的结果是，数组第一位存储了之前最后一位的值，最后一位变成最大值。这个最大值固定住，继续前边n-1个值的排序，也就是新的完全二叉树的堆化。重复这个过程，直到二叉树只剩根节点，而此时，经过n-1次置换，数组从小到大有序。

整个代码的核心是大顶堆化函数maxheapify。我写的这个函数没有使用递归，而普遍见到的写法是递归调用自身。如下：

def maxheapify(lst, n, father):
    left = 2 * i + 1
    right = 2 * i + 2
    maxindex = father
    if left and lst[left] > lst[maxindex]:
        maxindex = left
    if right and lst[right] > lst[maxindex]:
        maxindex = right
    if maxindex != father:
        lst[father], lst[maxindex] = lst[maxindex], lst[father]
        maxheapify(lst, n, maxindex)

两者(我写的和上边这个)是等价的。因为递归本身就是一种循环，尤其当原始问题分解后的算法一致的子问题，其个数小于2个时。这种情况下，迭代循环和递归之间的转换很好写。

堆排序的平均时间复杂度亦为nlogn，但也不如快排好用。原因是堆化函数可能使原本接近有序的数组反而变得更无序，另外父子节点这种跳着访问的方式对内存的使用不友好。所以堆排序的真实性能稍差。

堆排序容易掉的坑有不少，①是heap_sort函数里那个循环的起始和终止位。起点为n-1，代表数组最后位置；终点为1，代表数组第二位，因为数组首位始终要参与交换。所以，range(n-1,0,-1)。②是maxheap_build函数里那个循环的起始和终止位置。起点是capacity//2-1，理由是通过最后一个叶子节点位置可以计算得到最末一个父节点，而其后全部为叶子节点，因此不存在堆化需要；终点为0，代表根节点。所以，range(capacity//2-1,-1,-1)。这就是自上而下建堆原理，它可以保证整个完全二叉树彻底堆化。如果不这样逐个逆序遍历父节点，直接调用maxheapify(lst,n,0)，虽然可以从根节点堆化，但很大概率会半途中断，如中途遇见某个父节点恰好大于左右儿子，但左右子节点却小于孙节点。这就导致出现不彻底的堆化。于是建堆失败。③是maxheapify函数里的两个if条件判断，须注意它们应该是and语句，特别是left和right不能缺少。

堆排序内容差不多就这样，最后附一个自下而上(二叉堆视角)、从前向后(数组视角)的建堆代码。

def maxheap_build(lst):
    capacity = len(lst)
    for i in range(1, capacity):
        while True:
            baba = (i+1)//2-1
            if baba > 0 and lst[i] > lst[baba]:
                lst[i], lst[baba] = lst[baba], lst[i]
                i = baba
            if baba <= 0 or lst[i] <= lst[baba]:
                break

由此可见，所谓‘自上而下’指的是已知father，推出左右儿子left和right；所谓‘自下而上’指的是已知儿子节点，倒推父节点baba。如果使用自下而上构建堆，则用不上堆化函数maxheapify，无法复用即意味着多写代码。当然，也可以重写堆化函数。但自下而上堆化的算法比较笨，远不如自上而下省时省力。

The last but not the least，小顶堆排序整体上和大顶堆排序类似，唯一差别就是最后加上一句lst.reverse()。多此一举，所以堆排序一般就是大顶堆排序。