setvalue函数_如此搞定描点法画函数图像【多种函数适用】——GeoGebra制作教程...

上一篇说到可以通过输入框来改变参变量的值。那么，如果函数表达式、自变量x的取值都可以通过输入框来改变，那不就是一个GeoGebra文件可以搞定多种函数图像了吗？

来看看效果：

---

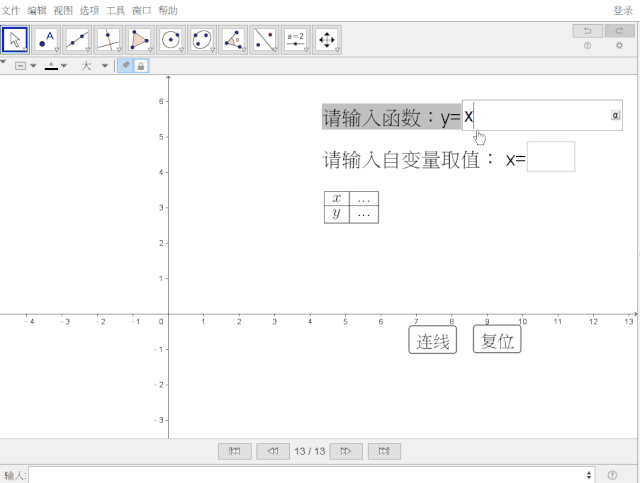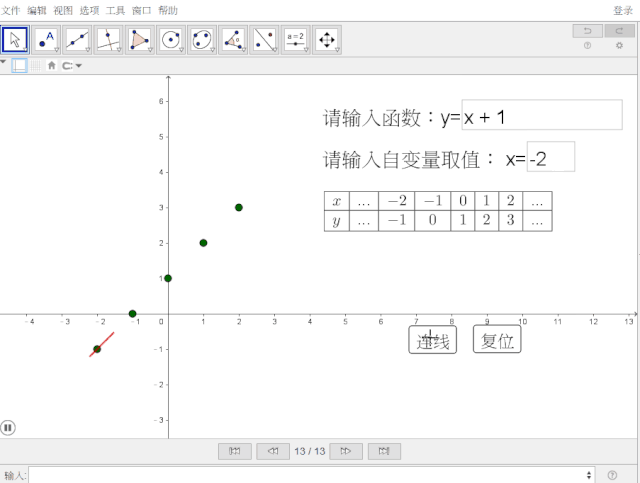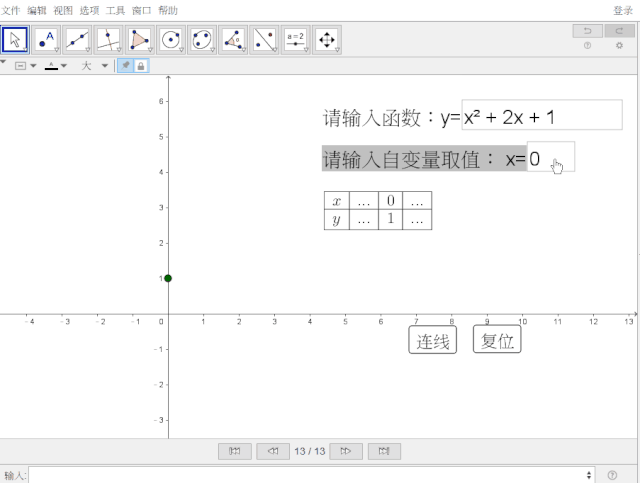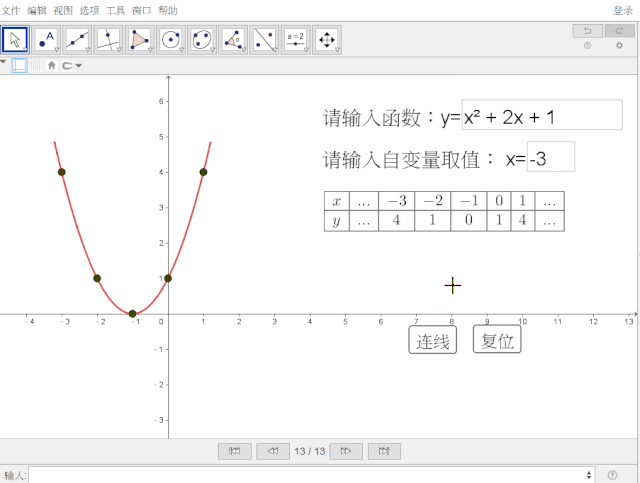
我们知道创建输入框时，选择关联对象，便可通过输入框的输入，改变所关联的对象。于是，制作思路由此开始。

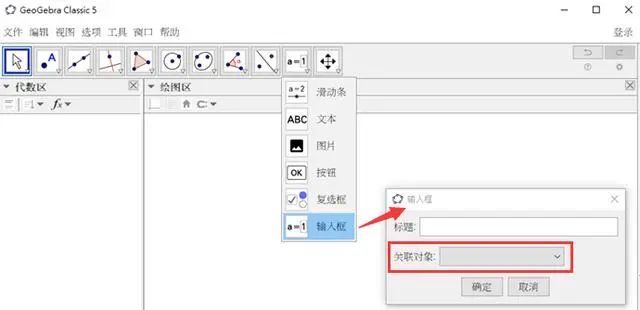
思路概要

1. 通过输入框1，输入函数解析式——需要函数f(x) = x【以下将 f(x) 简称为 f ,这里任意函数均可，因为在输入框一输入，函数 f 就跟着改变了】。

2. 通过输入框2，输入自变量x的取值——需要数值a=0【同样，a 为任意数值均可】。

3. 每次输入自变量x的取值，应有一个列表来存放——需要列表l1 = {}【即l1在原始状态时，是不含元素的列表】

创建相关对象

所有指令如下图所示，左边为指令，右边为相应的注释。 教程图【回复多种函数可获取word版】

不用急着看懂教程图，需结合输入框、按钮才能理解。这只是为方便叙述，才将所有指令先放上来。

创建输入框2

输入框2的标题为： 请输入自变量取值：x=

关联对象为：a

那么，如何做到通过输入框2的输入，轻松存放一系列自变量x的取值？这自然需要在该输入框的脚本里写东西了！

怎么写呢？先介绍个指令：追加(append)

追加( , )

也就是在已有列表的最后一个元素的后面，再加上对象。举例请见图：

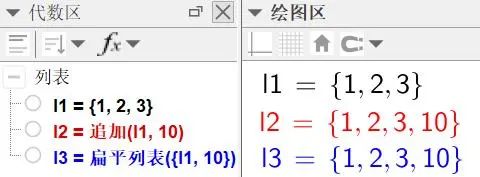例子

而我们已有列表l1 = {}，直接写指令追加(l1,a)即可吗？绝对不是的，这样一写，指令追加(l1,a)会产生一个新的列表(上图已说明了这一点)。而且输入框2一输入数值，a就会随之变化，根本无法保存已输入的数值。这个时候，就需要赋值(setvalue)指令上场了！只要把追加(l1,a)赋值给l1，即可解决问题，所以——

在输入框2的单击时脚本输入：赋值(l1,追加(l1,a))

有了这个输入框2，再回头看上面的教程图，好理解多了吧？如果不能理解，建议先看上一篇。

看完教程图，我们接着做！

创建按钮button1

【备注：在GeoGebra中，按钮名称默认为button1，button2，...】

标题：复位

单击时脚本：

l1={}

设置可见性(g, 1, false)

复位按钮，顾名思义是使所有对象回归初始状态，所以，列表l1={}，这里的 g 即 g(x) ,隐藏 g 也就是隐藏了函数图像。

创建按钮button2

标题： 连线

单击时脚本：

1. 设置可见性(g, 1, true)

2. k=滑动条(最小值(l1) - 0.2, 最大值(l1) + 0.2)

3. 设置可见性(k, 1, false)

4. 赋值(k,最小值(l1) - 0.2)

5. 启动动画(k)

这里的序号是为了方便看。然而，为什么需要写这么多条指令？

1. 第一条指令与button1相对应，是为了显示函数图像。

2. 为什么需要重新定义滑动条k？这是因为运行button1后，l1回归初始状态，不含任何元素，自然不存在l1的最小值、最大值，所以原先滑动条k的定义自然不起作用了，故需要再次定义。

3. 为什么要隐藏滑动条k？这是因为再次定义滑动条k后，滑动条会在绘图区中显示出来。

4. 第四条指令是为第五条指令服务的——先让k变成最小值，才好开始连线！

创建输入框1

终于轮到输入框1了！为什么现在才说到，请注意其脚本。

标题：请输入函数：y=

关联对象：f

单击时脚本输入：运行单击脚本(button1)

这里的脚本使得当改变函数解析式时，让所有对象回归到初始状态。

运行单击脚本(RunClickScript)指令，相当于点击按钮的效果。

---

至此，终于完成作品了！

小拓展1

对比这一篇和上一篇的做法，你觉得哪一种做法更好？又或是各有优势？

这一篇的作品效果是列表和描点同时进行，如果需要先列表，后描点，仿照上一篇即可。

小拓展2

为什么标题里说这是适用于多种函数的描点法画函数图像，而不是所有函数？

想一想，如果输入的是三角函数，会如何？

其结果是，列表变得非常不可爱——显示的是小数，这自然不是我们想要的效果。所以才说这一篇的做法是适用于多种函数，如果想要适用于三角函数，这就涉及到文本方面的修改了。

感谢您的关注与支持~

文章首发于头条号：啊K数学

【如有疑问，请在GeoGebra数学主页上留言，或点击