点到直线的投影公式_MIT—线性代数笔记16 投影矩阵和最小二乘法

第16讲 投影矩阵和最小二乘法

Projection matrices and least squares

网易公开课​open.163.com

• 投影 Projections

上一讲介绍了投影矩阵

，当它作用于向量

b，相当于把 b投影到矩阵 A的列空间。

如果向量b本身就在A列空间之内，即存在x使得Ax=b，则有：

如果向量b与A的列空间正交，即向量b在矩阵A的左零空间N(A)中，则有

• 最小二乘法 Least Squares

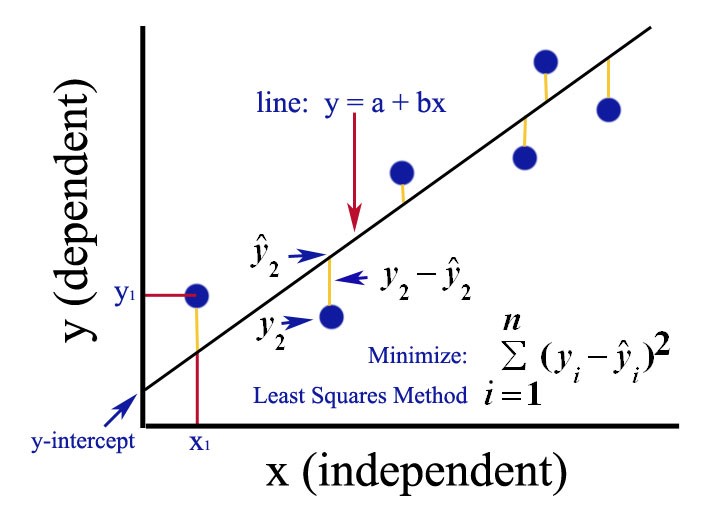
应用投影矩阵求方程组最优解的方法，最常用于“最小二乘法”拟合曲线。

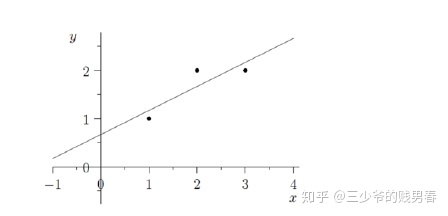
三个点{(1,1), (2,2), (3,2)}，求直线方程b=C+Dt，要求直线尽量接近于三个点。

C+ D=1

C+2D=2

C+3D=2

矩阵形式为

这个的方程Ax=b是无解的，解决办法就是求其最优解，最优解的含义即为误差最小，这里误差就是每个方程误差值的平方和

，因此就是寻找具有最小误差平方和的解

x，这就是所谓的“最小二乘”问题。

从几何上讨论求解过程，就是试图寻找数据点到直线距离的平方和

最小的情况，此时得到的C+Dt分别为p1，p2和p3，它们是满足方程并最接近于

b的结果。另一种看法是，对于 R3空间上的向量 b，它投影到矩阵 A的列空间中会得到向量 p=[p1 p2 p3]，投影到矩阵 A的零空间中则为 e。

现在求解

和

p。

方程

还可以从误差最小的角度出发求解：

对等号右边的表达式求偏导数，极值出现在偏导数为0的位置。求偏导最终会得到相同的线性方程组和相同的解。

得到直线表达式y=2/3+t/2。将t=1, 2, 3分别代入可得：

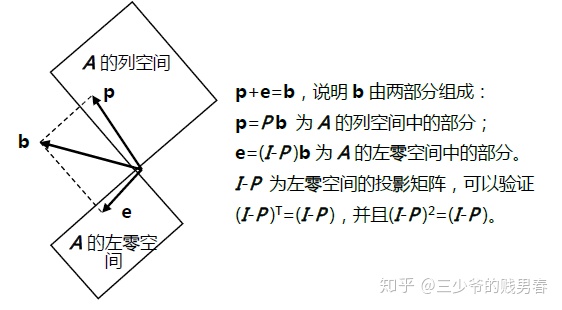
可以验证，向量p与e正交，并且e与矩阵A的列空间正交。

• 矩阵

证明：若A的列向量线性无关时，矩阵

为可逆矩阵。

假设存在x使得

。则有

，因此

Ax= 0。因为 A的列向量线性无关，所以只有当 x= 0时有 Ax= 0。因此只有当 x= 0时有

。即矩阵

为可逆矩阵。

如果矩阵的列向量是互相垂直的单位向量，则它们一定是线性无关的。我们将这种向量称之为标准正交（orthonormal）。

例如：

，

和

。还有

和

。