qcustomplot绘制动态曲线_【高等数学】Geogebra绘制旋转曲面

为了看起来习惯，只考虑

面上的曲线

绕

轴旋转，形成的旋转曲面。

用 Geogebra 实现的基本步骤是：

（i）将曲线

表示为空间曲线的参数方程形式；

（ii）用【曲线】命令绘制曲线：

曲线(x(t), y(t), z(t), t, t起始值, t终止值)

（iii）用【曲面】命令旋转出曲面：

曲面(曲线, 旋转角度, 旋转轴)

另外，为了能让图形动起来，可以将“曲线中的参数”和“旋转角度”设为【滑动条】。

下面通过 4 个实例来看一下：

例1（同济版8.5例3） 两条相交直线，夹角为

, 旋转成圆锥面（同济版8.5例3）

将直线

作为

轴，

将夹角

用【滑动条】表示，范围从

到

;

（1）将

表示为空间曲线的参数方程形式

借助图形来看，

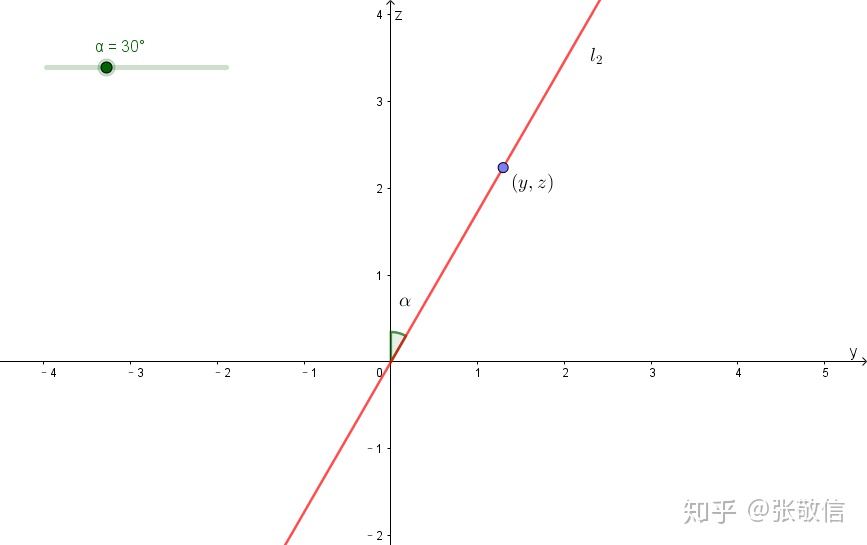
（2）用【曲线】命令绘制曲线：

曲线((0, t tan(α), t), t, -5, 5)

（3）用【曲面】命令旋转出曲面：

旋转角度

用【滑动条】表示，范围从

到

;

曲面(a, θ, z轴)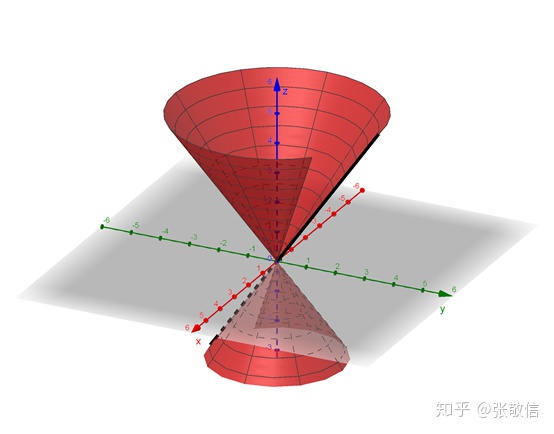

拖动

就可以观察旋转曲面动态生成的过程。

例2 用半圆旋转成球面。

（1）

面上的半圆：

改写成空间曲线的参数方程形式：

（2）用【曲线】命令绘制曲线：

曲线((0, R cos(t), R sin(t)), t, -π/2, π/2)

（3）用【曲面】命令旋转出曲面：

旋转角度

用【滑动条】表示，范围从

到

;

曲面(a, θ, z轴)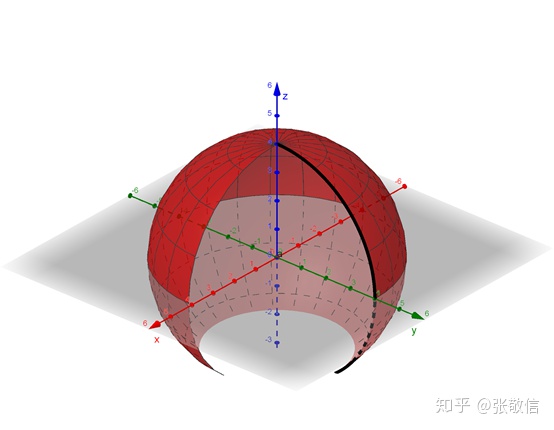

拖动

就可以观察旋转曲面动态生成的过程。

例3 用半支双曲线旋转成单叶双曲面。

（1）

面上半支双曲线：

改写成参数方程形式：

（2）用【曲线】命令绘制曲线：

曲线((0, a sec(t), b tan(t)), t, -π/2, π/2)

（3）用【曲面】命令旋转出曲面：

旋转角度

用【滑动条】表示，范围从

到

;

曲面(c, θ, z轴)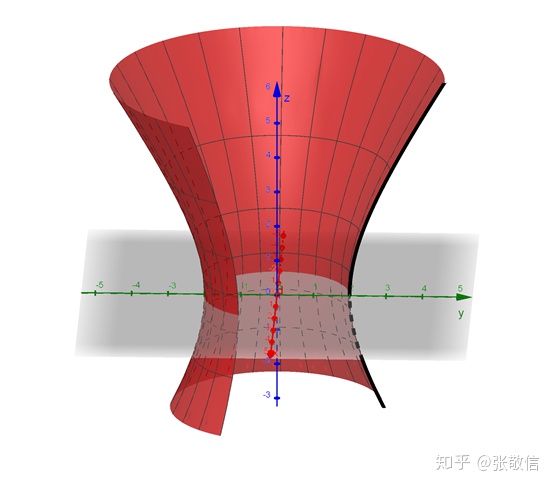

例4（同济版8.6图8-55） 两条异面直线旋转，得到单叶双曲面。

（1）直线参数方程直接给了，

（2）用【曲线】命令绘制曲线：

曲线((1, t, 2t), t, -5, 5)

（3）用【曲面】命令旋转出曲面：

旋转角度

用【滑动条】表示，范围从

到

;

曲面(a, θ, z轴)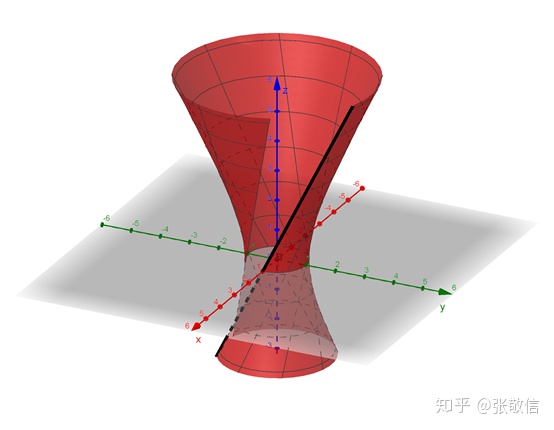

——————————————————————

原创作品，转载请注明。