圆内接四边形周长最大_圆的周长公式怎么来的？看完分分钟涨知识

原创不易，且写且珍惜。关注一下，给您惊喜。

话说，有一天，"无所不能"的爸爸在给小明辅导功课。

爸爸：“你看吧，这个路程就是这个半圆的周长，我们知道圆的周长计算公式为：C = 2πr = πd.......”

“爸爸，圆的周长公式怎么来的？”一脸天真的小明，托着腮帮，好奇地打断。

爸爸想了一会儿，憋着通红的脸，说到：“这是定理！”

不料，小明追问：“那定理又是怎么来的？”

爸爸：。。。。。。

好吧，为了避免上述尴尬，本期谷老师通过借助“阿基米德”和“刘微”(九章算术)的分析，来说明这个公式的推导思路，分享给大家。

每天叫醒你的不是闹钟，而是梦想和态度

难易指数：★★★★★★(超难度)

适宜对象：小学培优

本期编号：D00016

证明：圆的周长 C = 2πr = πd。(其中r为圆的半径，d为直径)

背景：

圆是一种几何图形。根据定义，通常用圆规来画圆。  同圆内圆的直径、半径的长度永远相同，圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。  同时，圆又是“正无限多边形”，而“无限”只是一个概念。当多边形的边数越多时，其形状、周长、面积就都越接近于圆。所以，世界上没有真正的圆，圆实际上只是概念性的图形。 (源自于“百度百科”)

原理说明：

1)高等数学”夹逼定理“简化版：(具体见本文后面说明)

如果A ≤ B ≤ C，且A=1，C=1，则B=1。

已知的求周长的几何图形，正多边形无疑是最简单的了，正三角形、正四边形、正五边形、正六边形……，但是乍一看，无论如何，我们也没法直接将圆和正多边形联系在一起，然而，根据夹逼定理，我们可以想象，用圆内接正多边形和外切正多边形，来辅助求解。

2)另外还需要知道的基本原理是：直角三角形的边角关系及勾股定理

a)直角三角形中，三边的关系为：

a² + b² = c²，其中c为斜边。

b)直角三角形30°、60°、45°，角边关系，分别为斜边的0.5、1.732、1.414倍。

解答：

根据上述分析，分别用多边形去内接或外切“单位圆”，如下。

1)三角形：

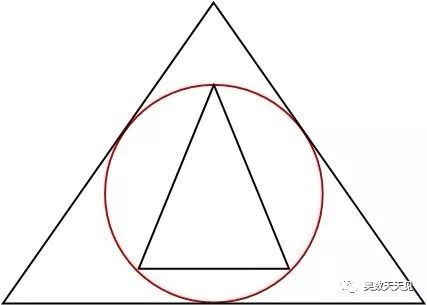
2)正方形：

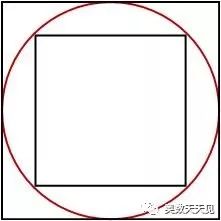
3)正五边形

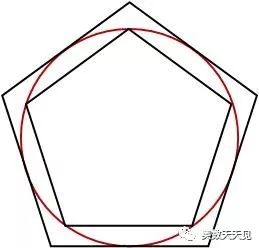
4)正六边形

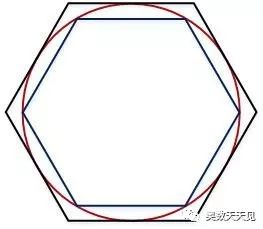
5)正八边形

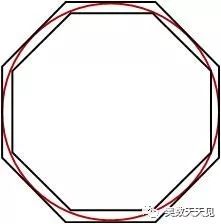
6)正十边形

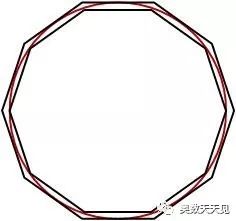
7)正12边形

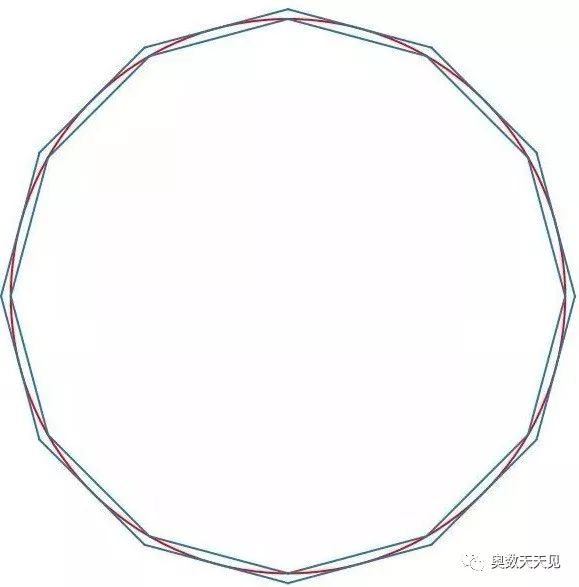
8)正96边形，已经看不清了，基本就是一个圆了。

从上图多边形的接入过程可知，多边形的周长越来越接近圆的周长。因此求圆的周长，就转换了求正多边形的周长，也就是正多边形的边长。

验算

下面我们用正六边形来验证，用正六边形去接入”单位圆”，此时有：

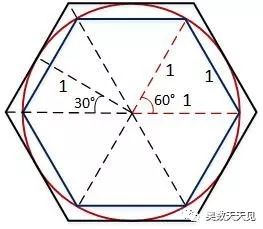
1)内接正六边形由6个正三角形组成，因此，其周长为6。

2)圆外切正6边形的边长为：2×1.732÷3=1.1546，周长为6.928。

3)用公式计算的圆周长为，2×3.1415 = 6.283，在[6, 6.928]之间。

继续上述步骤验算

依次计算12边形、24边形、36边形、96边形，可以算得周长越来越接近6.283 = 2×3.1415×1，而：π=3.1415，故圆的周长公式为：C = 2πr

总结

1)大多数学生都不知道公式怎么来的，只知道死记硬背。

2)了解公式和原理的来龙去脉，比刷题更有意义。

同类拓展：

1.“那年春，夫子去国游历，遇桃山美酒，遂寻径登山赏桃品酒，一路摘花饮酒而行，始切一斤桃花，饮一壶酒，后夫子惜酒，故再切一斤桃花，只饮半壶酒，再切一斤桃花，饮半半壶酒，如是而行……至山顶，夫子囊中酒尽，惘然四顾，问：一共切了几斤桃花，饮了几壶酒？”

长篇玄幻小说《将夜》，作者猫腻，2018年

答案：夫子饮 2 壶酒，斩尽满山桃花。

2.分析刘徽“割圆术”证明圆周长公式思路。

“近十期”精彩回顾

D00015期：等差数列(7种解法)

D00014期：巧算(台湾小学数学竞赛)

D00013期：圆的周长 (美国 AMC8竞赛)

D00012期：最大公约数(分而治之算法)

D00011期：算式谜

D00010期：计数问题(广度优先搜索算法)

D00009期：定义新运算(美国AMC 10A竞赛)

D00008期：孙子问题 (《算法导论》余数问题)

D00007期：年龄问题(美国 AMC 10A竞赛)

D00006期：工程问题

更多精彩内容，请通过公众号菜单进入

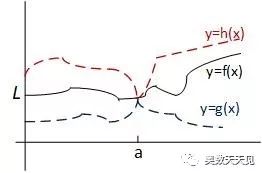
夹逼定理

三明治定理(又称夹逼定理)说的是，如果一个函数f被夹在函数g和h之间，当x-->a时，这两个函数g和h都收敛于同一个极限L，那么当x-->a时，f也收敛于极限L。

《普林斯顿 微积分读本》[美] Adrian Banner 3.6节

下图是对该定理的具体的描述。

圆周率π

圆周率，在古代的时候就已经非常的普遍应用了，特别是在历法和天文领域，当时职能部门也是通过圆周率进行演算。不过关于圆周率的精准数值，当时很多数学家经过悉心研究计算也一直没有答案。当时中国作为世界上的发达国家，地大物博，拥有很多位杰出的数学家，在数学方面，也是世界上最早研究的国家之一，早在《九章算术》中，就有数学家提出圆周率=3的观点。 后来，一直到东汉时期，这里就需要提到另一位非常杰出的数学家——张衡，当时他通过计算，将圆周率定位到了3.162，这个数值在我们眼中肯定是不准确的，但是在当时来讲，却已经非常令人震惊了。后来到了三国鼎立时期，又有数学家将这个数值精算到了3.155，这也为后来祖冲之精算圆周率打下了基础。 南北朝时期著名的天文学家、数学家祖冲之，在前人的基础上，通过不断地演算，终于取得了2个近似数，这也便是我们上文提到的3.1415926-3.1415927，因为祖冲之这个惊人的发现，在当时做出了巨大的贡献，人们后来在制造量器的时候，应用祖冲之计算的圆周率，量出的数值也更加的准确。同时，因为祖冲之在圆周率方面取得的伟大成就，也为现代圆周率打下了夯实的基础。 在2019年3月份， 谷歌计算机已经将圆周率计算到了小数点后的31.4万亿位 ，而一直到现在，圆周率仍然在不停的计算之中。很多科学家都好奇，圆周率究竟能不能被算尽，而不断增加的数字，也让圆周率添加了很多神秘的色彩。 有人推测，圆周率中或许隐藏着整个宇宙的终极密码，而关于我们的一切，也都可以在圆周率中找到答案。比方说你的生日，你的银行卡密码等等，未来，当圆周率的奥秘被揭开之时，或许人类的文明也将进入到一个崭新的台阶。(此文摘自网络，忘了出处，如有侵权，实属抱歉)

刘徽简介

《九章算术》约成书于东汉之初，共有246个问题的解法。 在许多方面： 如解联立方程，分数四则运算，正负数运算，几何图形的体积面积计算等，都属于世界先进之列。 刘徽在曹魏景初四年注《九章算术注》。 但因解法比较原始，缺乏必要的证明，刘徽则对此均作了补充证明。在这些证明中，显示了他在众多方面的创造性贡献。他是世界上最早提出十进小数概念的人，并用十进小数来表示无理数的立方根。在代数方面，他正确地提出了正负数的概念及其加减运算的法则，改进了线性方程组的解法。在几何方面，提出了"割圆术"，即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法。他利用割圆术科学地求出了圆周率π=3.1416的结果。他用割圆术，从直径为2尺的圆内接正六边形开始割圆，依次得正12边形、正24边形……，割得越细，正多边形面积和圆面积之差越小，用他的原话说是“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”他计算了3072边形面积并验证了这个值。刘徽提出的计算圆周率的科学方法，奠定了此后千余年来中国圆周率计算在世界上的领先地位。 (摘自百度百科)

阿基米德(公元前287年—公元前212年)

伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称， 阿基米德和高斯、牛顿并列为世界三大数学家 。阿基米德曾说过：“ 给我一个支点，我就能撬起整个地球。” 阿基米德确立了静力学和流体静力学的基本原理。给出许多求几何图形重心，包括由一抛物线和其网平行弦线所围成图形的重心的方法。阿基米德证明物体在液体中所受浮力等于它所排开液体的重量，这一结果后被称为阿基米德原理。 阿基米德在数学上也有着极为光辉灿烂的成就，特别是在几何学方面。阿基米德的数学思想中蕴涵微积分，阿基米德的《方法论》中已经“十分接近现代微积分”，这里有对数学上“无穷”的超前研究，贯穿全篇的则是如何将数学模型进行物理上的应用。他所缺的是没有极限概念，但其思想实质却伸展到17世纪趋于成熟的无穷小分析领域里去，预告了微积分的诞生。 阿基米德还利用割圆法求得π的值介于3.14163和3.14286之间。另外他算出球的表面积是其内接最大圆面积的四倍，又导出圆柱内切球体的体积是圆柱体积的三分之二，这个定理就刻在他的墓碑上。 阿基米德研究出螺旋形曲线的性质，现今的“阿基米德螺线”曲线，就是因为纪念他而命名。另外他在《数沙者》一书中，他创造了一套记大数的方法，简化了记数的方式。 (摘自”百度百科“)

每日寄语：宝剑锋从磨砺出，梅花香自苦寒来。《警世贤文·勤奋篇》

怎么样？本期的"圆的周长"公式推导学会了吗？快快讲给孩子们听吧。

以上内容为“奥数天天见”原创

禁止擅自转载或抄袭，违者必究

如需转载，或有任何疑难问题，欢迎联系我们。