python 求两条曲线的交点_三个视频搞定：双曲线的焦点三角形、第二定义及其运用、切线方程、直线与双曲线交点、弦长通径特殊双曲线...

● 本文适合高二上学期、高三一轮复习的同学阅读。先看视频再看文字，看视频时注意利用暂停，想清楚每一步变形的依据。

01

双曲线中点弦斜率、焦点三角形、第二定义

视频讲解

1、双曲线中点弦斜率结论

2、双曲线焦点三角形相关结论

3、双曲线的第二定义

平面内，到给定一点及一直线的距离之比为常数e(e>1，即为双曲线的离心率)的点的轨迹称为双曲线。定点叫双曲线的焦点，定直线叫双曲线的准线。双曲线准线的方程为x=±a²/c(焦点在x轴上)或y=±a²/c(焦点在y轴上)。

02

直线与双曲线的交点

视频讲解

4、直线与双曲线的交点个数讨论

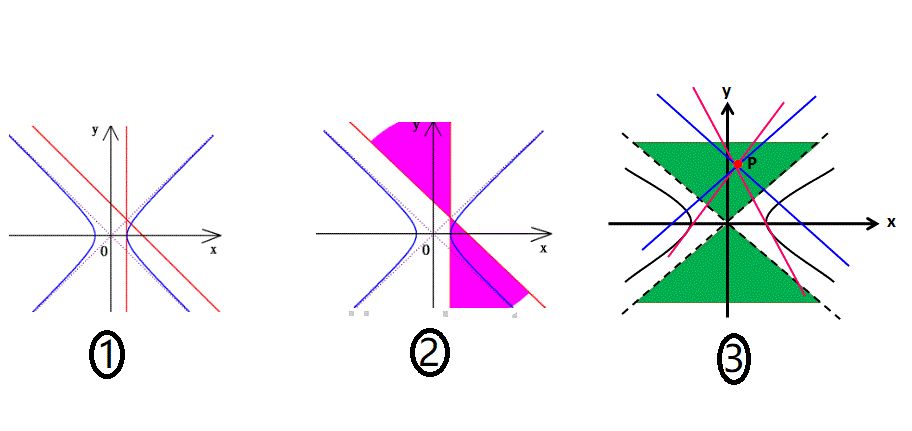
(1)代数法：联立双曲线与直线的方程组成二次方程组。解得有几组解就有几个交点。

(2)几何法：以焦点在Ｘ轴上的双曲线为例，

渐近线与双曲线没有公共点，平行于渐近线的直线与双曲线有一个公共点。

过原点与渐近线相交、斜率存在且不为0的直线和双曲线有0个或2个交点。

斜率为0的直线与双曲线有2个公共点。

垂直于Ｘ轴的直线与双曲线有0个、1个或2个公共点。

5、弦长公式

03

双曲线相关和识小结

视频讲解

6、双曲线通径、焦点三角形、弦长公式、切线方程

双曲线的通径：过焦点，垂直于实轴的弦即通径，通径有两条，长为2b²/a。

7、等轴双曲线、共轭双曲线、共渐近线双曲线

等轴双曲线：一种特殊的双曲线，特点是渐近线互相垂直，半实轴长与半虚轴长相等。

共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线叫做原双曲线的共轭双曲线，也可以看做把双曲线方程中的正负号交换了位置后得到的新双曲线方程，这两种方程的双曲线通常称它们互为共轭双曲线。

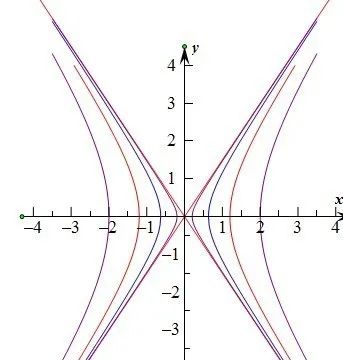
渐近线：如果双曲线上的一点沿着双曲线趋于无穷远时，该点与某条直线的距离趋于零，则称此条直线为双曲线的渐近线。

(本文部分图片与视频来自于网络，仅供学习交流用，若有不妥，请联系删除。)

人生有缘才相遇 扫码相识更有趣

微信号 :rong19711107 

公众号：周老师松果数学

● 扫码联系我

zlssgsx