语音计算矩形面积_如何计算广义球面矩形的面积

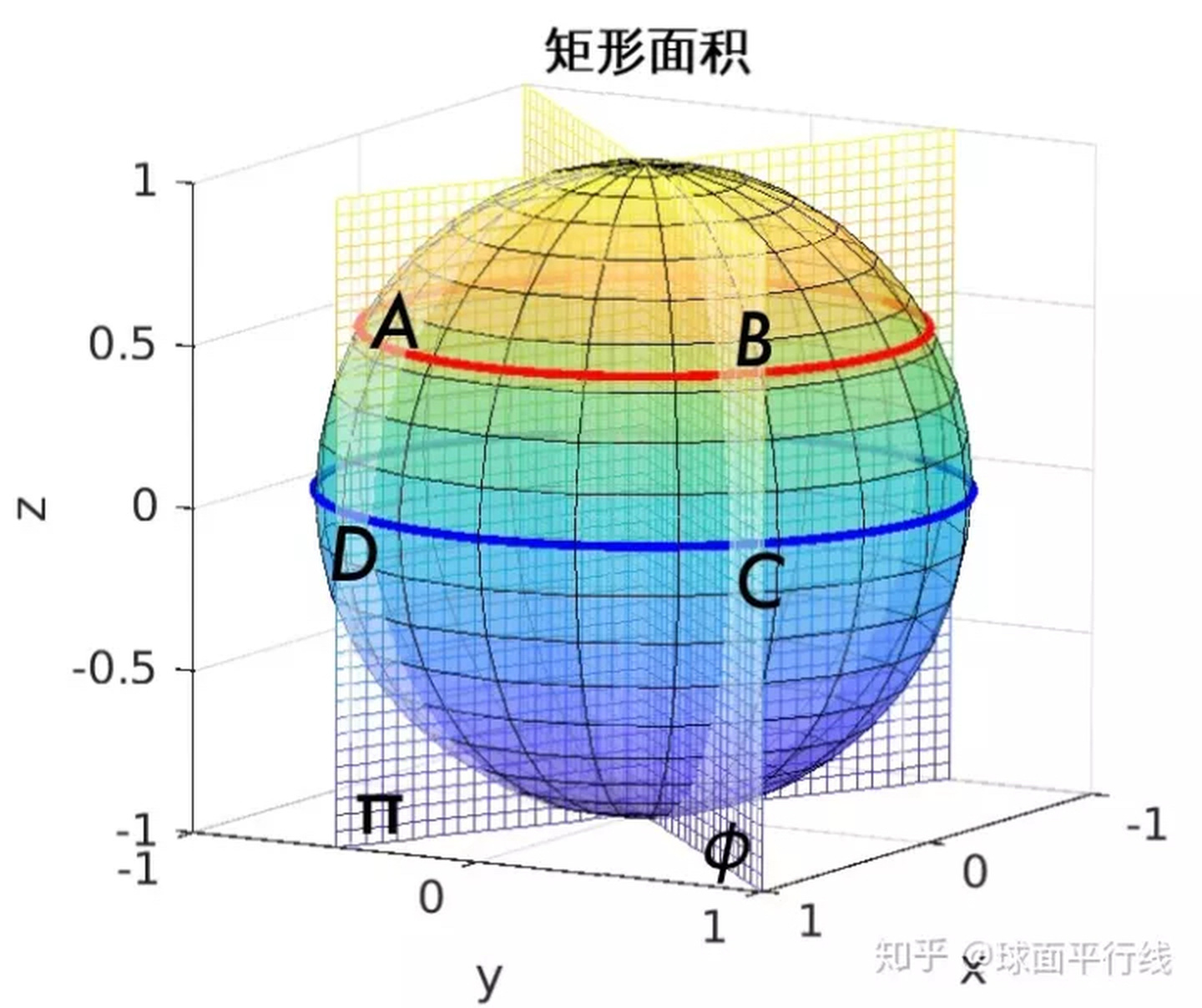
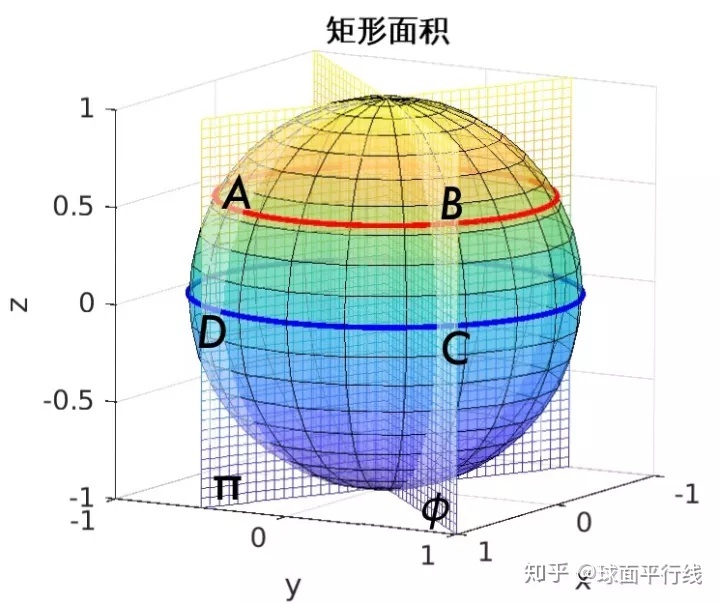
如图，DC为赤道上的圆弧，AB为纬线上的圆弧，两个平面π和φ分别通过两极切割球面，形成割线AD和BC，显然，DC、AD、BC皆为大圆弧。我们称四边形ABCD为广义球面矩形。

这个矩形的面积如何计算呢？

用矩形在纬度线上的弧长与Δβ的乘积，然后求和就可以得到矩形的面积，也就是

S=∫αcosβdβ

=αsinβ+C ^[1]

其中α是两个面π与φ的夹角，也就是维度线在矩形中的弧长。cosβ为矩形中不同纬度线上的纬度圆的半径。

如果β为纬度线AB的纬度，那么这个广义矩形面积为

S=αsinβ

可见，若这个广义矩形处于非常小的区域，那么在单位球面上其面积就是αβ。αβ是什么？就是这个矩形的长与宽的积。也就是说，平面矩形的面积为广义球面矩形的面积的特例。

图四

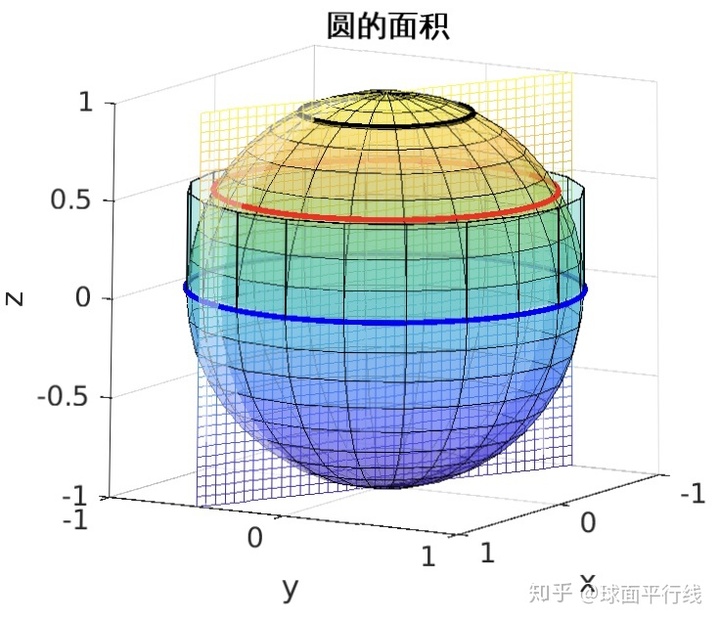
由广义矩形的公式可见，红色圆以下赤道以上的区域的球面面积（也是在整个圆周上的广义矩形的面积）等于与球等径且高度为sinβ的圆柱面的面积。同样，而整个球面的面积等于与球等径且高度等于圆柱面的面积。

参考

1. ^关于球面广义矩形面积积分公式 https://zhuanlan.zhihu.com/p/147184449