分析化学中的数字可以分为两种:一种为非测量所得的自然数,例如,测量次数、试样份数等;另一种为测量所得,即测量值或者数据计算的结果,其数据位数多少应与分析方法的准确度及其仪器的精密度相适应。
所谓的有效数字是指实际能测量的数字,测量数据不仅仅表示数量的大小,且能反映测量的不确定程度。所得数据的最后一位可能有上下一个单位的误差,我们将其称为不确定数字。有效数字包括所有的准确数字和最后一位不确定数字。分析实验中记录数据,有效数字的位数应根据测定方法和所用仪器的精确度来确定,只有一位不确定的数字,既不能夸大,也不能缩小测量的准确性,有效数字的位数反映了测量和结果的准确程度,绝不能随意增加或者减少。
1.1 有效数字的表示
为了取得准确的分析结果,不仅要准确地测量,而且还要正确地记录和计算。即记录的数字不仅表示数量的大小,而且要正确地反映测量的精确程度。例如,由于分析天平的感量是±0.000 1 g,在读出和记录质量时应该保留至小数点后面的第4位数字。若标定某溶液的浓度,用分析天平称取了基准物质,应记录为1.001 0 g,这一数值中,1.001是准确的,最后一位数字(0)是可疑的,可能有上下一个单位的误差。由于不确定数字所表示的量是客观存在的,仅因为受到仪器、量器的刻度精细程度的限制,在估计时受到观测者主观因素的影响而不能对它准确认定,因此它仍然是一位有效数字。在读出和记录质量时应该保留至小数点后面的第4位数字。
因此,有效数字是由全部准确数字和最后一位(只能是一位)不确定数字组成,它们共同决定了有效数字的位数。
有效数字位数的多少反映了测量的准确度,例如,用分析天平称取1.001 0 g试样,一般情况下称量的绝对误差为±0.000 2 g,那么相对误差为: 若用台秤称取试样1.0g,称量的绝对误差为±0.2g,那么相对误差为:
若用台秤称取试样1.0g,称量的绝对误差为±0.2g,那么相对误差为:
 由此可见,在测量准确度允许的范围内,数据中有效数字的位数越多,表明测定的准确度越高。
应当注意的是,数字后面的“0”也体现了一定的测量准确度,因而不可任意取舍。对于数据中的“0”,是否作为有效数字要具体情况具体分析。例如,各数有效数字的位数见表。
由此可见,在测量准确度允许的范围内,数据中有效数字的位数越多,表明测定的准确度越高。
应当注意的是,数字后面的“0”也体现了一定的测量准确度,因而不可任意取舍。对于数据中的“0”,是否作为有效数字要具体情况具体分析。例如,各数有效数字的位数见表。
 上述情况表明,数字之间与数字后的“0”是有效数字,因为它们是由测量所得到的。而数字前面的“0”是起定位作用的,它的个数与所取的单位有关而与测量的准确度无关,因而不是有效数字。例如,20.00 mL,改用L为单位时,表示成0.020 00 L,有效数字均是四位。上述数据中的最后两个,其有效数字的位数都比较模糊,例如,2 600,一般可视为四位。如果根据测量的实际情况,采用科学计数法将其表示成
2.6×103,2.60×103或2.600×103
则分别表示二、三或四位有效数字,其位数就明确了。
对于如分数、倍数关系等非测量值,由于它们没有不确定性,其有效数字可视为无限多位,类似地还有数学常数π、e等。
pH、pc、1gK等对数和负对数值,其有效数字的位数仅取决于对数值中尾数部分的位数,因其首数部分只说明了该数据的方次。例如,[H+]=0.002 0 mol/L,也可写成2.0×10-3 mol/L或pH =2.70,其有效数字均为两位。
上述情况表明,数字之间与数字后的“0”是有效数字,因为它们是由测量所得到的。而数字前面的“0”是起定位作用的,它的个数与所取的单位有关而与测量的准确度无关,因而不是有效数字。例如,20.00 mL,改用L为单位时,表示成0.020 00 L,有效数字均是四位。上述数据中的最后两个,其有效数字的位数都比较模糊,例如,2 600,一般可视为四位。如果根据测量的实际情况,采用科学计数法将其表示成
2.6×103,2.60×103或2.600×103
则分别表示二、三或四位有效数字,其位数就明确了。
对于如分数、倍数关系等非测量值,由于它们没有不确定性,其有效数字可视为无限多位,类似地还有数学常数π、e等。
pH、pc、1gK等对数和负对数值,其有效数字的位数仅取决于对数值中尾数部分的位数,因其首数部分只说明了该数据的方次。例如,[H+]=0.002 0 mol/L,也可写成2.0×10-3 mol/L或pH =2.70,其有效数字均为两位。
 1.2 准确度与精密度的关系
准确度和精密度是两个不同的概念,准确度可用误差来衡量。测量值与真实值越接近,误差就越小,测量越准确。精密度可用偏差来衡量。各测量值之间越接近,偏差就越小,精密度越高。
准确度和精密度是从不同侧面反映了分析结果的可靠性。前者反映了系统误差和随机误差的综合;后者反映了随机误差的大小。两者的关系可以用下面的例子说明,如图所示甲、乙、丙、丁四人测定结果的比较。
1.2 准确度与精密度的关系
准确度和精密度是两个不同的概念,准确度可用误差来衡量。测量值与真实值越接近,误差就越小,测量越准确。精密度可用偏差来衡量。各测量值之间越接近,偏差就越小,精密度越高。
准确度和精密度是从不同侧面反映了分析结果的可靠性。前者反映了系统误差和随机误差的综合;后者反映了随机误差的大小。两者的关系可以用下面的例子说明,如图所示甲、乙、丙、丁四人测定结果的比较。
 .表示个别测定值,|表示平均值
表示甲、乙、丙、丁四人测定同一标准试样 中某组分的质量分数时所得的结果(设其真实值为27.40%)。其中甲的结果的准确度和精密度均很好,结果可靠;乙的精密度虽好,但准确度低;丙的准确度和精密度都很差;丁的精密度很差,数据的可信度低,虽然其平均值接近真实值,但几个数据彼此相差很远,而仅是由于止负误差相互抵消才凑巧使结果接近真实值,因而丁的分析结果也是不可靠的。
综上所述:
①精密度是保证准确度的先决条件。精密度差,所测结果不可靠,就失去了衡量准确度的前提。
②高的精密度不一定能保证高的准确度,但可以找出精密度不高的原因,而后加以校正,从而提高分析结果的准确度和精密度,使测定结果既精密又准确。
1.3 随机误差的正态分布
由于随机误差的存在性,对同一试样在相同条件下进行多次测定,当测量次数趋于无穷大时,测量数据一般服从正态分布,正态分布的函数式为:
.表示个别测定值,|表示平均值
表示甲、乙、丙、丁四人测定同一标准试样 中某组分的质量分数时所得的结果(设其真实值为27.40%)。其中甲的结果的准确度和精密度均很好,结果可靠;乙的精密度虽好,但准确度低;丙的准确度和精密度都很差;丁的精密度很差,数据的可信度低,虽然其平均值接近真实值,但几个数据彼此相差很远,而仅是由于止负误差相互抵消才凑巧使结果接近真实值,因而丁的分析结果也是不可靠的。
综上所述:
①精密度是保证准确度的先决条件。精密度差,所测结果不可靠,就失去了衡量准确度的前提。
②高的精密度不一定能保证高的准确度,但可以找出精密度不高的原因,而后加以校正,从而提高分析结果的准确度和精密度,使测定结果既精密又准确。
1.3 随机误差的正态分布
由于随机误差的存在性,对同一试样在相同条件下进行多次测定,当测量次数趋于无穷大时,测量数据一般服从正态分布,正态分布的函数式为:
 说明:①y为概率密度,它是测量值x的函数。
②u为n→∞时测量值的平均值,称为总体平均值,表示测量值的集中趋势。若没有系统误差的情况下,u就是真实值。
③σ为总体标准偏差,表示数据的离散程度。
若以测量值x(或随机误差(x-u)为横坐标,概率密度y为纵坐标作图,可得正态分布曲线,如图所示测量值或误差的正态分布曲线。
说明:①y为概率密度,它是测量值x的函数。
②u为n→∞时测量值的平均值,称为总体平均值,表示测量值的集中趋势。若没有系统误差的情况下,u就是真实值。
③σ为总体标准偏差,表示数据的离散程度。
若以测量值x(或随机误差(x-u)为横坐标,概率密度y为纵坐标作图,可得正态分布曲线,如图所示测量值或误差的正态分布曲线。
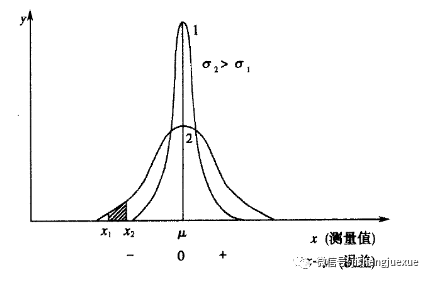 正态分布曲线与横坐标所夹的总面积表示所有测量值出现的概率总和,其值为1。概率密度函数对某区间(x1,x2)定积分就是测量值出现在此区间内的概率,即阴影部分面积。观察图2-3,我们可以发现:
①曲线为钟形对称,在x=u处有最高点,说明测量值x在u附近出现的概率大,大多数的测量值都集中在算术平均值u的附近。
②曲线以x=u为对称轴,说明绝对值相同的正负误差出现的概率相等。
③曲线中间大,两头小,当x趋向于-∞或+∞时,曲线以x轴为渐近线,说明小误差出现的概率大,大误差出现的概率小,出现很大误差的概率极小。
④总体标准偏差,不同时,曲线也不同。σ越小,最高点概率密度y越大,曲线越瘦高,即测量值出现在u附近的概率越大,测量数据越集中。反之,σ越大,最高点概率密度y越小,曲线越扁平,测量值出现在u附近的概率越小,测量数据越分散。
⑤若已知u和σ,正态分布曲线的位置与形状即可确定下来,由于x,u和σ都是变量,为了方便计算测量值落在某区间内的概率,令
正态分布曲线与横坐标所夹的总面积表示所有测量值出现的概率总和,其值为1。概率密度函数对某区间(x1,x2)定积分就是测量值出现在此区间内的概率,即阴影部分面积。观察图2-3,我们可以发现:
①曲线为钟形对称,在x=u处有最高点,说明测量值x在u附近出现的概率大,大多数的测量值都集中在算术平均值u的附近。
②曲线以x=u为对称轴,说明绝对值相同的正负误差出现的概率相等。
③曲线中间大,两头小,当x趋向于-∞或+∞时,曲线以x轴为渐近线,说明小误差出现的概率大,大误差出现的概率小,出现很大误差的概率极小。
④总体标准偏差,不同时,曲线也不同。σ越小,最高点概率密度y越大,曲线越瘦高,即测量值出现在u附近的概率越大,测量数据越集中。反之,σ越大,最高点概率密度y越小,曲线越扁平,测量值出现在u附近的概率越小,测量数据越分散。
⑤若已知u和σ,正态分布曲线的位置与形状即可确定下来,由于x,u和σ都是变量,为了方便计算测量值落在某区间内的概率,令
 u是以总体标准偏差σ为单位的(x-u)值。以u为曲线的横坐标,以概率密度为纵坐标,绘成的曲线即为标准正态分布曲线。
2 有效数字的修约规则
在处理分析数据时,涉及的各测量值的有效数字位数可能不同。从误差传递原理可知,通过运算所得的结果,其误差总比个别测量的误差大。数据计算所得结果的误差取决于各测量值(特别是误差较大的测量值)的误差。所以,为保证计算结果的准确度与实验数据相符合,则需要对其有效数字的位数确定,多余部分一概舍弃,我们将该过程称为数字修约。其基本原则如下:
2.1 采用“四舍六入五留双”的规则
该规则规定:当多余位数的首位≤4时,舍去;多余位数的首位≥6时,进位;等于5时,如果5后数字不为0,则进位;如果5后数字为0,则视5前面是奇数还是偶数,采用“奇进偶舍”的方法进行修约,是被保留数据的末位为偶数。
u是以总体标准偏差σ为单位的(x-u)值。以u为曲线的横坐标,以概率密度为纵坐标,绘成的曲线即为标准正态分布曲线。
2 有效数字的修约规则
在处理分析数据时,涉及的各测量值的有效数字位数可能不同。从误差传递原理可知,通过运算所得的结果,其误差总比个别测量的误差大。数据计算所得结果的误差取决于各测量值(特别是误差较大的测量值)的误差。所以,为保证计算结果的准确度与实验数据相符合,则需要对其有效数字的位数确定,多余部分一概舍弃,我们将该过程称为数字修约。其基本原则如下:
2.1 采用“四舍六入五留双”的规则
该规则规定:当多余位数的首位≤4时,舍去;多余位数的首位≥6时,进位;等于5时,如果5后数字不为0,则进位;如果5后数字为0,则视5前面是奇数还是偶数,采用“奇进偶舍”的方法进行修约,是被保留数据的末位为偶数。
例如,将下列数据修约为两位有效数字: 7.549→7.5 3.3690→3.4 7.4501→7.5 0.007350→0.0074 0.8450→0.84 2.2 禁止分次修约 修约应一次到位,不得连续多次进行修约,例如,将数据2.345 7修约为两位,则为2.345 7→2.3;然而若分次修约:2.345 7→2.346→2.35→2.4这样出现了错误。 2.3 可多保留一位有效数字进行运算 在大量运算中,为了提高运算速度,且又不使修约误差迅速累积,则可采用“安全数字”。即将参与运算各数的有效数字修约到比绝对误差最大的数据多保留一位,再运算后,将结果修约到应有的位数。例如,计算5.3527、2.3、0.054及3.35的和。按加减法的运算法则,其计算结果只保留一位小数。在计算过程中我们不妨多保留一位,则上述数据计算,可写成 5.35+2.3+0.05+3.35=11.05 计算结果可修约为11.0。 2.4 修约标准偏差 对标准偏差的修约,其结果应使准确度降低。例如,某计算结果的标准偏差为0.213,取两位有效数字,修约为0.21。在做统计检验时,标准偏差可多保留1~2位数参与运算,计算结果的统计量可多保留一位数字与临界值比较。
2.2.2.5与标准限度值比较时不应修约在分析测定中常需要将测定值与标准限度进行比较,从而确定样品是否合格。
有效数字位数的多少反映了测量的准确度,例如,用分析天平称取1.001 0 g试样,一般情况下称量的绝对误差为±0.000 2 g,那么相对误差为:
 若用台秤称取试样1.0g,称量的绝对误差为±0.2g,那么相对误差为:
若用台秤称取试样1.0g,称量的绝对误差为±0.2g,那么相对误差为:
 由此可见,在测量准确度允许的范围内,数据中有效数字的位数越多,表明测定的准确度越高。
应当注意的是,数字后面的“0”也体现了一定的测量准确度,因而不可任意取舍。对于数据中的“0”,是否作为有效数字要具体情况具体分析。例如,各数有效数字的位数见表。
由此可见,在测量准确度允许的范围内,数据中有效数字的位数越多,表明测定的准确度越高。
应当注意的是,数字后面的“0”也体现了一定的测量准确度,因而不可任意取舍。对于数据中的“0”,是否作为有效数字要具体情况具体分析。例如,各数有效数字的位数见表。
 上述情况表明,数字之间与数字后的“0”是有效数字,因为它们是由测量所得到的。而数字前面的“0”是起定位作用的,它的个数与所取的单位有关而与测量的准确度无关,因而不是有效数字。例如,20.00 mL,改用L为单位时,表示成0.020 00 L,有效数字均是四位。上述数据中的最后两个,其有效数字的位数都比较模糊,例如,2 600,一般可视为四位。如果根据测量的实际情况,采用科学计数法将其表示成
2.6×103,2.60×103或2.600×103
则分别表示二、三或四位有效数字,其位数就明确了。
对于如分数、倍数关系等非测量值,由于它们没有不确定性,其有效数字可视为无限多位,类似地还有数学常数π、e等。
pH、pc、1gK等对数和负对数值,其有效数字的位数仅取决于对数值中尾数部分的位数,因其首数部分只说明了该数据的方次。例如,[H+]=0.002 0 mol/L,也可写成2.0×10-3 mol/L或pH =2.70,其有效数字均为两位。
上述情况表明,数字之间与数字后的“0”是有效数字,因为它们是由测量所得到的。而数字前面的“0”是起定位作用的,它的个数与所取的单位有关而与测量的准确度无关,因而不是有效数字。例如,20.00 mL,改用L为单位时,表示成0.020 00 L,有效数字均是四位。上述数据中的最后两个,其有效数字的位数都比较模糊,例如,2 600,一般可视为四位。如果根据测量的实际情况,采用科学计数法将其表示成
2.6×103,2.60×103或2.600×103
则分别表示二、三或四位有效数字,其位数就明确了。
对于如分数、倍数关系等非测量值,由于它们没有不确定性,其有效数字可视为无限多位,类似地还有数学常数π、e等。
pH、pc、1gK等对数和负对数值,其有效数字的位数仅取决于对数值中尾数部分的位数,因其首数部分只说明了该数据的方次。例如,[H+]=0.002 0 mol/L,也可写成2.0×10-3 mol/L或pH =2.70,其有效数字均为两位。
 1.2 准确度与精密度的关系
准确度和精密度是两个不同的概念,准确度可用误差来衡量。测量值与真实值越接近,误差就越小,测量越准确。精密度可用偏差来衡量。各测量值之间越接近,偏差就越小,精密度越高。
准确度和精密度是从不同侧面反映了分析结果的可靠性。前者反映了系统误差和随机误差的综合;后者反映了随机误差的大小。两者的关系可以用下面的例子说明,如图所示甲、乙、丙、丁四人测定结果的比较。
1.2 准确度与精密度的关系
准确度和精密度是两个不同的概念,准确度可用误差来衡量。测量值与真实值越接近,误差就越小,测量越准确。精密度可用偏差来衡量。各测量值之间越接近,偏差就越小,精密度越高。
准确度和精密度是从不同侧面反映了分析结果的可靠性。前者反映了系统误差和随机误差的综合;后者反映了随机误差的大小。两者的关系可以用下面的例子说明,如图所示甲、乙、丙、丁四人测定结果的比较。
 .表示个别测定值,|表示平均值
表示甲、乙、丙、丁四人测定同一标准试样 中某组分的质量分数时所得的结果(设其真实值为27.40%)。其中甲的结果的准确度和精密度均很好,结果可靠;乙的精密度虽好,但准确度低;丙的准确度和精密度都很差;丁的精密度很差,数据的可信度低,虽然其平均值接近真实值,但几个数据彼此相差很远,而仅是由于止负误差相互抵消才凑巧使结果接近真实值,因而丁的分析结果也是不可靠的。
综上所述:
①精密度是保证准确度的先决条件。精密度差,所测结果不可靠,就失去了衡量准确度的前提。
②高的精密度不一定能保证高的准确度,但可以找出精密度不高的原因,而后加以校正,从而提高分析结果的准确度和精密度,使测定结果既精密又准确。
1.3 随机误差的正态分布
由于随机误差的存在性,对同一试样在相同条件下进行多次测定,当测量次数趋于无穷大时,测量数据一般服从正态分布,正态分布的函数式为:
.表示个别测定值,|表示平均值
表示甲、乙、丙、丁四人测定同一标准试样 中某组分的质量分数时所得的结果(设其真实值为27.40%)。其中甲的结果的准确度和精密度均很好,结果可靠;乙的精密度虽好,但准确度低;丙的准确度和精密度都很差;丁的精密度很差,数据的可信度低,虽然其平均值接近真实值,但几个数据彼此相差很远,而仅是由于止负误差相互抵消才凑巧使结果接近真实值,因而丁的分析结果也是不可靠的。
综上所述:
①精密度是保证准确度的先决条件。精密度差,所测结果不可靠,就失去了衡量准确度的前提。
②高的精密度不一定能保证高的准确度,但可以找出精密度不高的原因,而后加以校正,从而提高分析结果的准确度和精密度,使测定结果既精密又准确。
1.3 随机误差的正态分布
由于随机误差的存在性,对同一试样在相同条件下进行多次测定,当测量次数趋于无穷大时,测量数据一般服从正态分布,正态分布的函数式为:
 说明:①y为概率密度,它是测量值x的函数。
②u为n→∞时测量值的平均值,称为总体平均值,表示测量值的集中趋势。若没有系统误差的情况下,u就是真实值。
③σ为总体标准偏差,表示数据的离散程度。
若以测量值x(或随机误差(x-u)为横坐标,概率密度y为纵坐标作图,可得正态分布曲线,如图所示测量值或误差的正态分布曲线。
说明:①y为概率密度,它是测量值x的函数。
②u为n→∞时测量值的平均值,称为总体平均值,表示测量值的集中趋势。若没有系统误差的情况下,u就是真实值。
③σ为总体标准偏差,表示数据的离散程度。
若以测量值x(或随机误差(x-u)为横坐标,概率密度y为纵坐标作图,可得正态分布曲线,如图所示测量值或误差的正态分布曲线。
 正态分布曲线与横坐标所夹的总面积表示所有测量值出现的概率总和,其值为1。概率密度函数对某区间(x1,x2)定积分就是测量值出现在此区间内的概率,即阴影部分面积。观察图2-3,我们可以发现:
①曲线为钟形对称,在x=u处有最高点,说明测量值x在u附近出现的概率大,大多数的测量值都集中在算术平均值u的附近。
②曲线以x=u为对称轴,说明绝对值相同的正负误差出现的概率相等。
③曲线中间大,两头小,当x趋向于-∞或+∞时,曲线以x轴为渐近线,说明小误差出现的概率大,大误差出现的概率小,出现很大误差的概率极小。
④总体标准偏差,不同时,曲线也不同。σ越小,最高点概率密度y越大,曲线越瘦高,即测量值出现在u附近的概率越大,测量数据越集中。反之,σ越大,最高点概率密度y越小,曲线越扁平,测量值出现在u附近的概率越小,测量数据越分散。
⑤若已知u和σ,正态分布曲线的位置与形状即可确定下来,由于x,u和σ都是变量,为了方便计算测量值落在某区间内的概率,令
正态分布曲线与横坐标所夹的总面积表示所有测量值出现的概率总和,其值为1。概率密度函数对某区间(x1,x2)定积分就是测量值出现在此区间内的概率,即阴影部分面积。观察图2-3,我们可以发现:
①曲线为钟形对称,在x=u处有最高点,说明测量值x在u附近出现的概率大,大多数的测量值都集中在算术平均值u的附近。
②曲线以x=u为对称轴,说明绝对值相同的正负误差出现的概率相等。
③曲线中间大,两头小,当x趋向于-∞或+∞时,曲线以x轴为渐近线,说明小误差出现的概率大,大误差出现的概率小,出现很大误差的概率极小。
④总体标准偏差,不同时,曲线也不同。σ越小,最高点概率密度y越大,曲线越瘦高,即测量值出现在u附近的概率越大,测量数据越集中。反之,σ越大,最高点概率密度y越小,曲线越扁平,测量值出现在u附近的概率越小,测量数据越分散。
⑤若已知u和σ,正态分布曲线的位置与形状即可确定下来,由于x,u和σ都是变量,为了方便计算测量值落在某区间内的概率,令
 u是以总体标准偏差σ为单位的(x-u)值。以u为曲线的横坐标,以概率密度为纵坐标,绘成的曲线即为标准正态分布曲线。
2 有效数字的修约规则
在处理分析数据时,涉及的各测量值的有效数字位数可能不同。从误差传递原理可知,通过运算所得的结果,其误差总比个别测量的误差大。数据计算所得结果的误差取决于各测量值(特别是误差较大的测量值)的误差。所以,为保证计算结果的准确度与实验数据相符合,则需要对其有效数字的位数确定,多余部分一概舍弃,我们将该过程称为数字修约。其基本原则如下:
2.1 采用“四舍六入五留双”的规则
该规则规定:当多余位数的首位≤4时,舍去;多余位数的首位≥6时,进位;等于5时,如果5后数字不为0,则进位;如果5后数字为0,则视5前面是奇数还是偶数,采用“奇进偶舍”的方法进行修约,是被保留数据的末位为偶数。
u是以总体标准偏差σ为单位的(x-u)值。以u为曲线的横坐标,以概率密度为纵坐标,绘成的曲线即为标准正态分布曲线。
2 有效数字的修约规则
在处理分析数据时,涉及的各测量值的有效数字位数可能不同。从误差传递原理可知,通过运算所得的结果,其误差总比个别测量的误差大。数据计算所得结果的误差取决于各测量值(特别是误差较大的测量值)的误差。所以,为保证计算结果的准确度与实验数据相符合,则需要对其有效数字的位数确定,多余部分一概舍弃,我们将该过程称为数字修约。其基本原则如下:
2.1 采用“四舍六入五留双”的规则
该规则规定:当多余位数的首位≤4时,舍去;多余位数的首位≥6时,进位;等于5时,如果5后数字不为0,则进位;如果5后数字为0,则视5前面是奇数还是偶数,采用“奇进偶舍”的方法进行修约,是被保留数据的末位为偶数。例如,将下列数据修约为两位有效数字: 7.549→7.5 3.3690→3.4 7.4501→7.5 0.007350→0.0074 0.8450→0.84 2.2 禁止分次修约 修约应一次到位,不得连续多次进行修约,例如,将数据2.345 7修约为两位,则为2.345 7→2.3;然而若分次修约:2.345 7→2.346→2.35→2.4这样出现了错误。 2.3 可多保留一位有效数字进行运算 在大量运算中,为了提高运算速度,且又不使修约误差迅速累积,则可采用“安全数字”。即将参与运算各数的有效数字修约到比绝对误差最大的数据多保留一位,再运算后,将结果修约到应有的位数。例如,计算5.3527、2.3、0.054及3.35的和。按加减法的运算法则,其计算结果只保留一位小数。在计算过程中我们不妨多保留一位,则上述数据计算,可写成 5.35+2.3+0.05+3.35=11.05 计算结果可修约为11.0。 2.4 修约标准偏差 对标准偏差的修约,其结果应使准确度降低。例如,某计算结果的标准偏差为0.213,取两位有效数字,修约为0.21。在做统计检验时,标准偏差可多保留1~2位数参与运算,计算结果的统计量可多保留一位数字与临界值比较。
2.2.2.5与标准限度值比较时不应修约在分析测定中常需要将测定值与标准限度进行比较,从而确定样品是否合格。
文章来源:《分析化学分析方法的原理及应用研究》







 本文探讨了分析化学中科学计数法如何保留有效数字,以及在进行数学运算时的有效数字规则。
本文探讨了分析化学中科学计数法如何保留有效数字,以及在进行数学运算时的有效数字规则。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








