PyTorch中的11种优化算法使用教程

---

1. 什么是优化器（Optimizer）

深度学习模型通过引入损失函数，用来计算目标预测的错误程度。根据损失函数计算得到的误差结果，需要对模型参数（即权重和偏差）进行很小的更改，以期减少预测错误。但问题是如何知道何时应更改参数，如果要更改参数，应更改多少？这就是引入优化器的时候了。简单来说，优化器可以优化损失函数，优化器的工作是以使损失函数最小化的方式更改可训练参数，损失函数指导优化器朝正确的方向移动。

Pytorch中的优化器：管理并更新模型中可学习参数（权重和偏差）的值，使得模型输出更接近真实标签。

• 导数：函数在指定坐标轴上的变化率；
• 方向导数：指定方向上的变化率；
• 梯度：一个向量，方向为方向导数取得最大值的方向。

优化器最主要的功能：

• 管理：优化器管理哪一部分参数；
• 更新：优化器通过优化策略更新模型中可学习参数的值，通常都会采用梯度下降法。

---

2. torch.optim

PyTorch Optimizer 官方文档：LINK。

2.1 Optimizer 的属性

PyTorch optimizers 基类。

torch.optim.Optimizer(params, defaults)

class Optimizer(object)
      def_init_(self,params,defaults):
      self.defaults=defaults
      self.state=defaultdict(dict)
      self.param_groups=[ ]
      ...
      param_groups=[{'params':param_groups}]

• defaults：优化器超参数；
• state：参数的缓存，如momentum的缓存；
• param_groups：管理的参数组；
• _step_count：记录更新次数，学习率调整中使用；

---

2.2 Optimizer 的方法

zero_grad()：清空所管理参数的梯度。

zero_grad()

由于Pytorch中的grad属性不自动清零，每次计算梯度后都会累加到grad属性中，造成错误；因此，在进行梯度求导（反向传播）之后，通过 zero_grad() 方法进行清零。

---

step()：执行一步更新。

step()

当计算出loss，并用loss进行反向传播求出各个参数的梯度之后，使用step()更新权值参数。step() 会采用梯度下降的策略。比如动量法，随机梯度下降，自适应学习率方法等。

---

add_param_group()：添加参数组。

add_param_group()

优化器管理很多参数，其中有些参数可以分组，对于不同组的参数，有不同的超参数设置，例如在某一模型中，希望特征提取部分的权值参数的学习率小一点，学习更新慢一点，这时可以把特征提取的参数设置为一组参数，而对于后面全连接层，希望其学习率大一点，学习快一点。这时，可以把整个模型参数设置为两组，一组为特征提取部分的参数，另一部分是全连接层的参数，对这两组设置不同的学习率或超参数，此时就需要用到参数组概念。

---

state_dict ()：获取优化器当前状态信息 字典

state_dict ()

load_state_dict()：加载状态信息字典

load_state_dict()：加载状态信息字典

以上两个方法用于保存模型某个状态的信息，可以在模型训练过程中，从断点处恢复训练。

---

3. 学习率

梯度下降（不带学习率参数的更新公式）：$w_{i+1}=w_i-g(w_i)$
假设有目标函数 $y=f(x)=4x^2$，求导后有 $y^{\prime }=f^{\prime }(x)=8x$。

下面计算梯度更新情况：

• $x_0=2，y_0=16，f^{\prime }(x_0)=16$
• $x_1=x_0-f^{\prime }(x_0)=2-16=-14$
• $x_1=-14，y_1=784，f^{\prime }(x_1)=-112$
• $x_2=x_1-f^{\prime }(x_1)=-14+112=98，y_2=38416$
• $......$

由以上推导可以看出，在更新到第二步时，梯度已经比较大了，预测值增加了几个数量级，出现了梯度爆炸的情况，这样会导致模型不可用。应对以上这种问题，通常还需要在权重更新时添加学习率参数，以控制更新的幅度。于是梯度更新公式变为：

• $w_{i+1}=w_i-LR\ast g(w_i)$

学习率直接影响模型能够以多快的速度收敛到局部最小值，即达到最好的精度。一般来说，学习率越大，神经网络学习速度越快。如果学习率太小，网络很可能会陷入局部最优；但是如果太大，超过了极值，损失就会停止下降，在某一位置反复震荡。

针对上文提到的目标函数，探究不同学习率的影响：

学习率 设置为 1：

学习率设置为 0.4 ：

学习率设置为 0.2：

学习率设置为0.1：

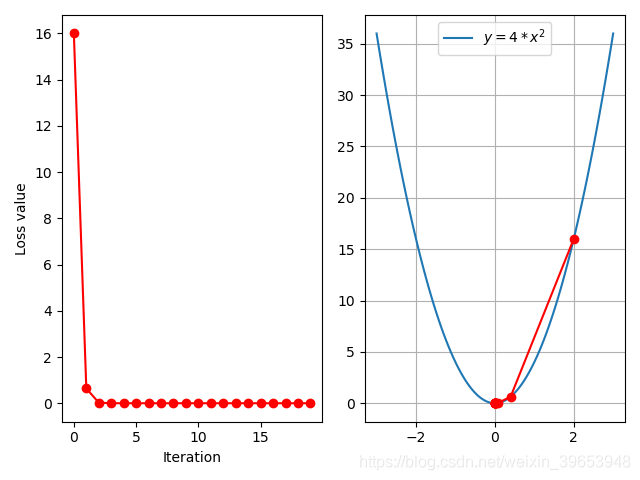
由以上分析可以看出，合适的学习率可以加快模型的收敛，该参数是模型优化过程中最重要的超参数之一。下面分析不同学习率的损失曲线：

上图进一步印证了学习率并非绝对的越大或越小就好，二是针对不同的数据集和模型有其最佳的学习率，针对本例的目标函数，最佳的学习率设置为 $0.125$ 左右。

---

4. Momentum

动量，冲量（Momentum）：结合当前梯度与上一次更新信息，用于当前更新。参数更新时在一定程度上保留之前更新的方向，同时又利用当前batch的梯度微调最终的更新方向，简言之就是通过积累之前的动量来加速当前的梯度。

图自：LINK

当一个小球从山上向下滚，没有阻力时，它的动量会越来越大（速度越来越快），但是如果遇到了阻力，速度就会变小。动量优化法就是借鉴此思想，使得梯度方向在不变的维度上，参数更新变快，梯度有所改变时，更新参数变慢，这样就能够加快收敛并且减少动荡。

其核心思想是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减，越近期的数据加权越重，但较旧的数据也给予一定的加权。

上式中，$v_t$ 是当前时刻的平均值，当前时刻的参数 ${\theta }_t$ ，其所占权重为 $1-\beta$，$\beta$ 是参数，$v_{t-1}$ 是上一时刻的平均值。假设要求第100天的平均气温 $v_{100}$，$v_t$ 表示到第$t$天的平均温度值，${\theta }_t$ 表示第$t$天的温度值，经过推导可以得到：
$$\sum _i^N(1-\beta )\ast {\beta }^i\ast {\theta }_{N-i}$$

将 $\beta$ 设置为 0.9，绘图得：

可以看出时间越远，对第100天温度的影响越小。下面探究一下不同 $\beta$ 值的影响：

$\beta$ 可以看作记忆周期，$\beta$ 越大，记忆周期越长，反之，越短。$\beta$ 通常设置为0.9，其物理意义为只关注十天左右的数据对当前的影响。

---

Momentum 更新公式：

• $v_i=m\ast v_{i-1}+g(w_i)$
• $w_{i+1}=w_i-lr\ast v_i$

其中 $w_{i+1}$ 表示第 $i+1$ 次更新的参数，$v_i$ 表示更新量，$m$ 表示衰减系数，$lr$ 表示学习率。

---

衰减系数对模型的影响：


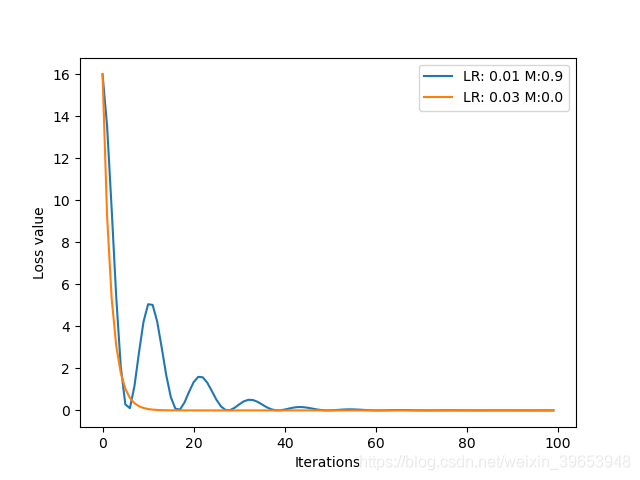
由上图可知，当动量比较大时，损失容易出现震荡；恰当的动量参数设置，可以使模型更快收敛。

---

5. PyTorch 优化器

优化器综述Paper：

A Survey of Optimization Methods from a Machine Learning Perspective

---

5.1 torch.optim.SGD

torch.optim.SGD 可实现SGD优化算法，带动量SGD优化算法，带 NAG(Nesterov accelerated gradient) 动量SGD优化算法，并且有 weight_decay 项。

torch.optim.SGD(params, 
                lr=<required parameter>, 
                momentum=0, 
                dampening=0, 
                weight_decay=0, 
                nesterov=False)

参数说明：

• params (iterable)：参数组，优化器要管理的那部分参数。
• lr (float)：初始学习率，可按需随着训练过程不断调整学习率。
• momentum (float)：动量，通常设置为0.9，0.8。
• dampening (float)：若采用 nesterov，dampening 必须为 0。
• weight_decay (float)：权值衰减系数，即L2正则项的系数。
• nesterov (bool)：bool，是否使用 NAG(Nesterov accelerated gradient)。

---

5.2 torch.optim.Adagrad

torch.optim.Adagrad(params, 
                    lr=0.01, 
                    lr_decay=0, 
                    weight_decay=0, 
                    initial_accumulator_value=0, 
                    eps=1e-10)

【Paper】：LINK

---

5.3 torch.optim.RMSprop

torch.optim.RMSprop(params, 
                    lr=0.01, 
                    alpha=0.99, 
                    eps=1e-08, 
                    weight_decay=0, 
                    momentum=0, 
                    centered=False)

【Paper】：LINK

---

5.4 torch.optim.Adadelta

torch.optim.Adadelta(params, 
                     lr=1.0, 
                     rho=0.9, 
                     eps=1e-06, 
                     weight_decay=0)

【Paper】：LINK

---

5.5 torch.optim.Adam(AMSGrad)

Adam是一种自适应学习率的优化方法，Adam利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。Adam 结合了 RMSprop 和 Momentum，并进行了偏差修正，是非常常用的优化算法。

torch.optim.Adam(params, 
                 lr=0.001, 
                 betas=(0.9, 0.999), 
                 eps=1e-08, 
                 weight_decay=0, 
                 amsgrad=False)

【Paper】：LINK

---

5.6 torch.optim.Adamax

torch.optim.Adamax(params, 
                   lr=0.002, 
                   betas=(0.9, 0.999), 
                   eps=1e-08, 
                   weight_decay=0)

【Paper】：LINK

---

5.7 torch.optim.SparseAdam

torch.optim.SparseAdam(params, 
                       lr=0.001, 
                       betas=(0.9, 0.999), 
                       eps=1e-08)

---

5.8 torch.optim.AdamW

torch.optim.AdamW(params, 
                  lr=0.001, 
                  betas=(0.9, 0.999), 
                  eps=1e-08, 
                  weight_decay=0.01, 
                  amsgrad=False)

【Paper】：LINK

---

5.9 torch.optim.ASGD

torch.optim.ASGD(params, 
                 lr=0.01, 
                 lambd=0.0001, 
                 alpha=0.75, 
                 t0=1000000.0, 
                 weight_decay=0)

【Paper】：LINK

---

5.10 torch.optim.LBFGS

torch.optim.LBFGS(params, lr=1, 
                  max_iter=20, 
                  max_eval=None, 
                  tolerance_grad=1e-07, 
                  tolerance_change=1e-09, 
                  history_size=100, 
                  line_search_fn=None)

---

5.11 torch.optim.Rprop

torch.optim.Rprop(params, 
                  lr=0.01, 
                  etas=(0.5, 1.2), 
                  step_sizes=(1e-06, 50))

---