分类变量编码在机器学习中的应用-CSDN博客

原文：HTML
原题：All about Categorical Variable Encoding：Convert a categorical variable to number for Machine Learning Model Building
作者：Baijayanta Roy
翻译校对：datamonday

文章目录

One Hot Encoding
Label Encoding
Ordinal Encoding
Helmert Encoding
Binary Encoding
Frequency Encoding
Mean Encoding
Weight of Evidence Encoding
Probability Ratio Encoding
Hashing
Backward Difference Encoding
Leave One Out Encoding
James-Stein Encoding
M-estimator Encoding
FAQ
Conclusion

在这里插入图片描述
大多数机器学习算法都无法处理分类变量，需要将它们转换为数值。许多算法的性能会根据分类变量的编码方式而有所不同。

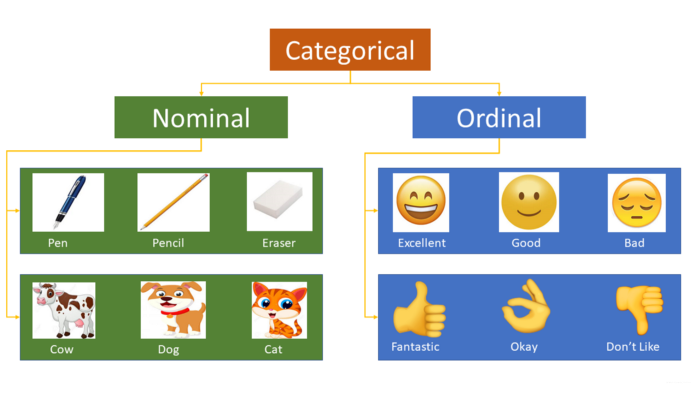
以下是标量（Nominal variable）的一些示例：

Red, Yellow, Pink, Blue
Singapore, Japan, USA, India, Korea
Cow, Dog, Cat, Snake

序数变量（Ordinal variables）的示例：

High, Medium, Low
“Strongly agree,” Agree, Neutral, Disagree, and “Strongly Disagree.”
Excellent, Okay, Bad

可以通过多种方式将这些分类变量编码为数值，这篇文章将介绍从基本到高级的大多数内容，包含以下编码方法：

One Hot Encoding
Label Encoding
Ordinal Encoding
Helmert Encoding
Binary Encoding
Frequency Encoding
Mean Encoding
Weight of Evidence Encoding
Probability Ratio Encoding
Hashing Encoding
Backward Difference Encoding
Leave One Out Encoding
James-Stein Encoding
M-estimator Encoding
Thermometer Encoder (To be updated)

为了说明起见，我将使用此数据表格（DataFrame），其包含两个独立变量或特征（温度和颜色）和一个标签（目标）。它还具有Rec-No，它是记录的序列号，共有10条记录。Python代码如下所示。

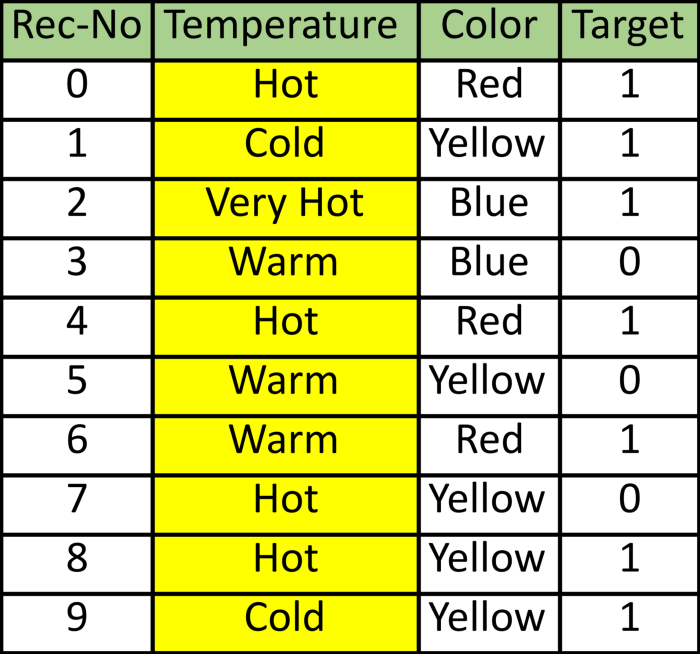
在这里插入图片描述

我们将使用Pandas和Scikit-learn和category_encoders（Scikit-learn贡献库）来显示Python中的不同编码方法。

One Hot Encoding

在这种方法中，将每个类别映射到一个包含1和0的矢量，表示该特征的存在与否。向量的数量取决于特征类别的数量。如果该特征类别的数量非常多，则此方法会产生很多列，从而大大降低学习速度。 Pandas的 get_dummies 函数可以将分类变量编码为哑变量：

在这里插入图片描述
Scikit-learn中的 OneHotEncoder 类也可以实现，但它不会创建其他特征列。

独热编码（One Hot Encoding）非常流行。可以用N-1(N=类别数)来表示所有类别，因为这足以对没有包含的类别进行编码。通常，对于回归，使用N-1（放弃独热编码新特征的第一列或最后一列），但对于分类，建议使用所有N列，因为大多数基于树的算法都是基于所有可用变量建立一棵树。在线性回归中应该使用具有N-1个二元变量的一热编码，以确保正确的自由度数（N-1）。线性回归在训练的过程中，可以获得所有的特征，因此会完全检查整个虚变量集。这意味着N-1个二元变量给线性回归提供了原始分类变量的完整信息（完全代表）。这种方法可以用于任何在训练过程中同时考察所有特征的机器学习算法。例如，支持向量机和神经网络以及和聚类算法。

在基于树的方法中，如果删除，将永远不会考虑该附加标签。因此，如果在基于树的学习算法中使用分类变量，则比较好的做法是将其编码为N个二进制变量，并且不要丢弃。

Label Encoding

在这种编码中，为每个类别分配了一个从1到N的值（N为特征的类别数）。这种方法的一个主要问题是这些类别之间没有关系或顺序，但是算法可能会将它们视为但是算法可能会将它们视为某种顺序，或者存在某种关系。在下面的示例中，它看起来像（Cold <Hot <Very Hot <Warm … 0 <1 <2 ❤️）。
在这里插入图片描述
Pandas的 factorize 也执行相同的功能。

在这里插入图片描述

Ordinal Encoding

我们执行序数编码以确保变量的编码保留变量的序数性质。正如我在本文开头提到的那样，这仅对序数变量合理。 这种编码看起来几乎与标签编码类似，但略有不同，因为标签编码不会考虑变量是否为序数，并且会分配整数序列：

as per the order of data (Pandas assigned Hot (0), Cold (1), “Very Hot” (2) and Warm (3)) or
as per alphabetical sorted order (scikit-learn assigned Cold(0), Hot(1), “Very Hot” (2) and Warm (3)).

如果我们以温度标尺为顺序，则顺序值应从“冷”到“非常热”。顺序编码会将值指定为 ( Cold(1) <Warm(2)<Hot(3)<Very Hot(4))。通常，我们从1开始进行序数编码。

使用Pandas引用此代码，首先，需要通过字典分配变量的原始顺序。然后按照字典映射变量的每一行。
在这里插入图片描述
尽管非常简单，但仍需要进行编码以告知序数值，以及按顺序从文本到整数的实际映射是什么。

Helmert Encoding

在此编码中，将某个级别的因变量的平均值与所有先前级别的因变量的平均值进行比较。

category_encoders中的版本有时称为反向Helmert编码。将某个级别的因变量平均值与之前所有级别的因变量平均值进行比较。因此，名称“reverse”用于区别于 forward Helmert编码。

在这里插入图片描述

Binary Encoding

二进制编码将类别转换为二进制数字。每个二进制数字创建一个特征列。如果存在n个唯一类别，则二进制编码将导致仅有log(base 2)ⁿ 个特征。在此示例中，有四个特征；因此，二进制编码特征的总数将是三个特征。 与“独热编码”相比，这将需要较少的特征列（对于100个类别，“独热编码”将具有100个特征，而对于“二进制”编码，我们将仅需要七个特征）。

对于二进制编码，必须遵循以下步骤：

首先，将类别转换为从1开始的数字顺序（顺序是在类别出现在数据集中时创建的，并不表示任何序数性质）。
然后，将这些整数转换为二进制代码，例如3变为011，4变为100。
然后，二进制数的数字形成单独的列。

请参考下图：
在这里插入图片描述
使用category_encoders包中的 BinaryEncoder 函数可以实现二进制编码。

Frequency Encoding

这是一种利用类别的频率作为标签的方法。 在频率与目标变量有些相关的情况下，它可以帮助模型根据数据的性质以正比例和反比例理解和分配权重。三个步骤：

选择要转换的分类变量
按类别变量分组并获得每个类别的计数
将其与训练数据集重新结合

在这里插入图片描述

Mean Encoding

平均编码或目标编码是Kagglers遵循的一种病毒（viral）编码方法。这有很多变化，我将介绍基本版本和平滑版本。平均编码与标签编码类似，只是这里的标签与目标直接相关。例如，在平均目标编码中，对于特征标签中的每一个类别，都是用目标变量在训练数据上的平均值来决定的。这种编码方法将相似类别之间的关系凸显出来，但联系被限定在类别和目标本身之内。平均目标编码的优点是不影响数据量，有助于加快学习速度。通常，Mean编码存在过拟合，因此，在大多数场合，使用交叉验证或其他方法进行正则化是必须的。平均数编码的方法如下：

1. 选择要转换的分类变量。
1. 按类别变量分组，并获得“目标”变量上的汇总和。（“温度”中每个类别的总数为1）
1. 按类别变量分组，并获得“目标”变量的总计数。
1. 划分第2步/第3步的结果，然后将其与训练集合并。

在这里插入图片描述
代码实现：

均值编码可以在标签中体现目标，而标签编码与目标不相关。在具有大量特征的情况下，均值编码可能被证明是更简单的选择。均值编码倾向于对类别进行分组，而在标签编码的情况下，分组是随机的。

实际上，此目标编码有多种变体，例如平滑。平滑可以实现如下：

在这里插入图片描述

Weight of Evidence Encoding

证据权重（WoE）是衡量分组技术区分好坏的“强度”的一种度量。开发此方法主要是为了建立一种预测模型，以评估信贷和金融行业中的贷款违约风险。 证据权重（WOE）用于衡量证据支持或破坏假设的程度。

其计算方法如下：
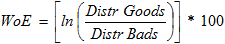
在这里插入图片描述
如果P(Goods) / P(Bads) = 1，则WoE将为0。也就是说，该组的结果是随机的。如果P(Bads) > P(Goods) ，则优势比将小于1，WoE将小于0；另一方面，如果一组中的P(Goods) > P(Bads)，则WoE> 0。

WoE非常适合Logistic回归，因为Logit变换只是几率的对数，即 ln(P(Goods)/P(Bads))。因此，通过在Logistic回归中使用WoE编码的预测变量，可以将所有预测变量准备和编码为相同的比例。线性逻辑回归方程中的参数可以直接比较。

WoE转换具有（至少）三个优点：

1）它可以转换自变量，以便与因变量建立单调关系。它所做的还不止于此：要确保单调关系，将其“重新编码”为任何有序的度量（例如1,2,3,4…）就足够了，但是WoE转换按“逻辑”规模对类别进行排序， Logistic回归很自然；
2）对于具有太多（稀疏填充）离散值的变量，可以将它们分为几类（密集填充），并且WoE可以用于表示整个类别的信息；
3）由于WoE是标准值，因此可以在类别和变量之间比较每个类别对因变量的（单变量）影响（例如，可以将已婚人员的WoE与体力劳动者的WoE进行比较）。

它还（至少）具有三个缺点：

1）由于归类为几个类别而导致的信息丢失；
2）这是一个“单变量”量度，因此未考虑自变量之间的相关性；
3）根据类别的创建方式，很容易操纵（过拟合）变量的影响。

下面代码片段说明了如何构建代码来计算WoE。
在这里插入图片描述

一旦为每个组计算WoE，我们就可以将其映射回Data-frame。
在这里插入图片描述

Probability Ratio Encoding

概率比编码与证据权重（WoE）类似，唯一的区别是仅使用了好坏概率之比。对于每个标签，我们计算target = 1的平均值，即平均值为 1 ( P(1) )，以及target = 0 ( P(0) )的概率。然后，我们计算比率P(1)/P(0)并用该比率替换标签。我们需要为P(0)添加一个最小值，以避免任何除以零的情况，其中对于任何特定类别，没有target = 0。

在这里插入图片描述

Hashing

散列将分类变量转换为整数的高维空间，其中分类变量的两个向量之间的距离大致保持了变换后的数字维空间。使用散列时，维度数量将远远少于像“独热编码”这样的编码方式的维度数量。当分类的基数非常高时，此方法很有用。

Backward Difference Encoding

在后向差分编码中，将一个级别的因变量的平均值与先前级别的因变量的平均值进行比较。这种类型的编码对于标称或有序变量可能有用。

该技术属于用于分类特征的对比度编码系统。 K个类别或级别的特征通常以K-1个虚拟变量序列的形式进入回归。

Leave One Out Encoding

这与目标编码非常相似，但是在计算某个级别的平均目标以减少离群值的影响时会排除当前行的目标。

James-Stein Encoding

对于特征值，James-Stein估计量返回的加权平均值为：

观察到的特征值的平均目标值。
平均目标值（与特征值无关）。
James-Stein编码器将平均值缩小为总体平均值。它是基于目标的编码器。但是，James-Stein估计量有一个实际限制-仅针对正态分布进行了定义。

M-estimator Encoding

M-Estimate编码器是目标编码器的简化版本。它只有一个超参数-m，代表正则化的功效。 m值越高，收缩越强。 m的推荐值在1到100的范围内。

FAQ

【常见问题解答01：我应该使用哪种方法？】

答：没有适用于每个问题或数据集的单一方法。你可能需要尝试一些才能看到效果更好的结果。一般准则是参考文章末尾显示的备忘单。

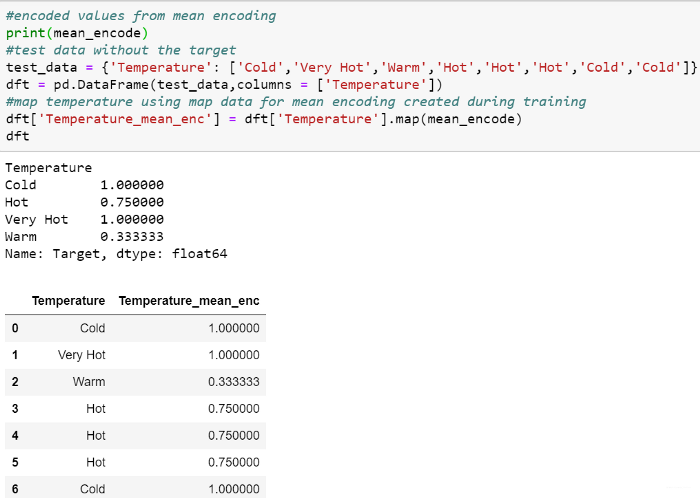
【常见问题解答02：如何针对情况（例如目标编码）创建分类编码，因为在测试数据中不会有任何目标值？】

答：我们需要使用训练时创建的映射值。此过程与缩放或规范化中的概念相同，在缩放或规范化中，我们使用训练数据来缩放或规范化测试数据。 W映射并在测试时间预处理中使用相同的映射。我们甚至可以为每个类别和映射值创建一个词典，然后在测试时使用该词典。在这里，我使用均值编码来解释这一点。

Training Time
在这里插入图片描述
Testing Time

Conclusion

对于所有机器学习模型，必须理解所有这些编码在所有情况下或对于每个数据集都无法正常工作。数据科学家仍然需要进行实验，并找出最适合其特定情况的方法。如果测试数据具有不同的类别，则其中某些方法将无法使用，因为功能将不相似。研究社区的基准出版物很少，但不是结论性的，效果最好。我的建议是尝试使用较小的数据集尝试每种方法，然后决定将重点放在调整编码过程上。可以使用下面的备忘单作为指导工具。
在这里插入图片描述