0/0型极限等于多少_两个重要极限的一点理解（下）

前言：对于第一个重要极限，我在上篇文章里已经提到过了写了一下我怎么理解的，链接如下：感兴趣的小伙伴可以观看一下：两个重要极限的一点理解(上)

今天的文章我想说说两个重要极限中第二个重要极限，如下

正文：

1.为什么等于e?

对于为什么等于e我在这里简单推导一下

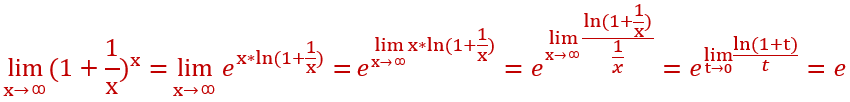
如果是新手一枚建议这个极限的推导过程自己动笔推一下

用到了e^lnx=x，以及等价无穷小替换当x趋于0时，ln(1+x)~x

2.还有其他变形形式吗？

这个应该是第二重要极限最常考的类型了吧

这到底跟上面的有哪些不同？

①x的趋向不同，一个趋向于0，一个趋向于∞

②一个以(1+1/x)为底，x为指数。另外一个以(1+x)，1/x为指数

本质这两个都是1的∞次方型，1+后面这项与次幂互为倒数

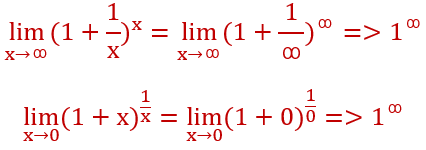
3.真假美猴王环节

这两个留给大家思考吧，看看跟上述的两个有什么不同之处，另外求出来极限是多少

4.一般解法

想想上大学的时候，老师教给你是怎么利用第二重要极限凑的？

举几个例题，如果之前没学过，建议一起学习

1.

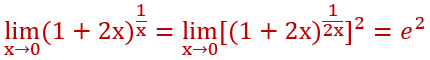
①首先带入x趋于0，验证是1的∞次方型

②然后2x与1/x并不互为倒数，于是调整次幂变成1/2x

③次幂*1/2，所以要再2次幂平衡系数

我总结的略显粗糙，但大概的思路和做题步骤就是这样的

2.

第二个题跟第一个题目难度一样，入门级别

3.

第三个题目相比较于前两个题目难度上了一个台阶，由于底数形式并不是1+x的形式，我们需要些技巧来进行把1凑出来，长期关注我的小伙伴知道，+n-n这个技巧很重要，经观察分子与分母只差了个常数，所以-7，+14为了平衡系数，凑出来1了拆项，互为倒数套公式进行计算

4.

这个看起来底数是三项，我们可以把后面的两项通分合成一项，然后与次幂凑互为倒数

再利用高次幂进行求极限，不要被它的外表所打倒

5.

没有1，就创造1，+1-1，然后用第二重要极限化简，对于这个题目而言还用到了第一重要极限，这个对于新手来说难度蛮高的，好好解吧，相信通过这几个题目对这个解题思路熟练掌握了

5.进阶思路

还有别的思路？对于老师教的方法而言，在凑倒数时耗费了大量的时间，有另外一种思考方式，如下

6.

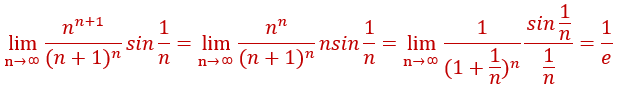
对于这个题目而言我想说的一点是

一定要区分开，这两个到底有什么不同之处，一个次幂是自变量，一个次幂为常数，所应用的公式也不一样，一个是高次幂而另外一个是重要极限，千万不要想当然

7.

这个题目需要你对等价无穷小替换的灵活掌握，不单单需要知道1-cosx等价于多少，还要对他的变形进行推导化简再利用第二重要极限进行求解

8.

这个题目稍微难了些，相比较其他题目来说上手比较难，首先底数1+就没有，需要凑1，然后想到等价无穷小公式a^x-1~xlna，再用对数的性质进行求解化简

9.

这样做对吗?答案肯定不对，首先你就不能人为改变先后求极限的顺序，需要同时对一个整体进行求极限

假设题目这样做就可以，两个不同的自变量分时求极限

那么对于这个题而言正确的做法是什么？

还是用的e^lnx=x，然后用的倒代换还有等价无穷小替换

x-ln(1+x)~(1/2)*x^2，考研党建议熟记这个替换公式

10.

最后算个小公式吧

上面是公式，下面是例题，可以看出d是无用的

那么我们用普通算法来验证一下这个结果对不对

一个是老师教的思路，一个是进阶思路，虽然看起来过程看起来一样长，但是缺省下了很长的时间不用来倒腾平衡次数了，你看第一种次幂我写了多长，容易出错，肯定有人问d为什么没用，d作为一个常数在用高次幂(x->∞)的时候，其结果都是最高次幂的系数之比，根本轮不到常数插手，高次幂其实就是分子分母同时除以最高次幂而已，所以d无用，任意常数值都可以，对结果不会造成影响，这个公式也可以记住，也可以不记，重要的是理解这个求解过程

对文章有什么疑问或错误，欢迎与我一起讨论

如果觉得文章还不错，点个打赏分享再走吧

笔耕不辍，有你支持