vc++画线段的函数_三个视频搞定三角函数（定义篇）：锐角、任意角三角函数、单位圆、三角函数线...

学习三角函数的定义，关键点在于通过数形结合来理解。做好了这一点，后续的深化、理解、记忆都将不是个事儿。

锐角三角函数的定义

视频：锐角三角函数的定义、识记与解直角三角形

1、锐角三角函数在直角三角形中定义。

    (1) 直角三角形中，三个角大小确定后，三边的比值关系也就确定了。由此可知，边的比值大小与角的大小存在对应关系。这种对应关系就是三角函数。     

(2)如上图，SinA=a/c(对边比斜边);                                   CosA=b/c(邻边比斜边);

                      tanA=a/b(对边比邻边)。

2、特殊三角板与特殊角的三角函数。我们手中常用的两个三角板三个角分别是：

30度、60度、90度；

45度、45度、90度。

三边比值关系确定(如下图)

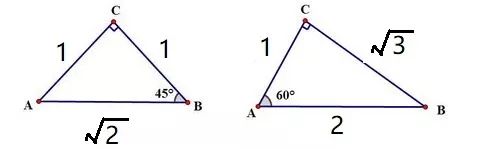
     通过锐角三角函数在直角三角形中的定义，结合特殊三角形边长比值关系，记住特殊锐角的三角函数值，将降低后续学习负担。

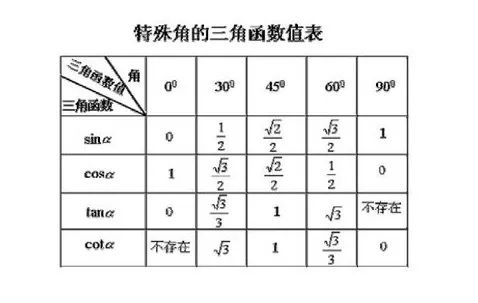
3、注意：视频中关于锐角三角函数用于解直角三角形的范例，是学习三角形问题转化方法的好素材。

 任意角三角函数的定义 

视频：任意角三角函数的定义与三角函数符号。

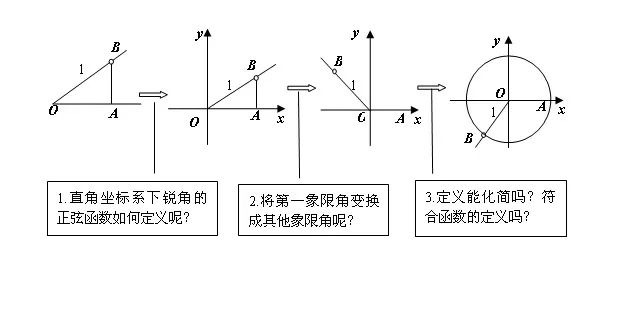
4、将角放入平面直角坐标系中，使角的顶点与坐标原点重合，角的始边与X轴非负半轴重合。在角的终边上任取一点P(x，y)，记点P到原点O的距离为r，则

SinA=y/r(纵比距);                                                      CosA=x/r(横比距);

                        tan A=y/x(纵比横)。

5、上述定义兼容了锐角三角函数在直角三角形中的定义。后续学习中有结论：求任何角的三角函数都能通过诱导公式转化为求锐角三角函数值来处理。

6、三角函数值与单位圆。

在任意角三角函数定义中，当所选的点为角的终边与单位圆的交点时，这时点的纵坐标为角的正弦值、横坐标为角的余弦值。(这种等价关系，在后续学习中，根据需要相互替代，会为让学习与计算更方便)

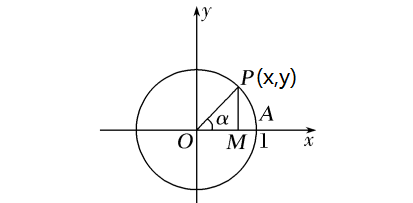
sina=y     cosa=x    tana=y/x

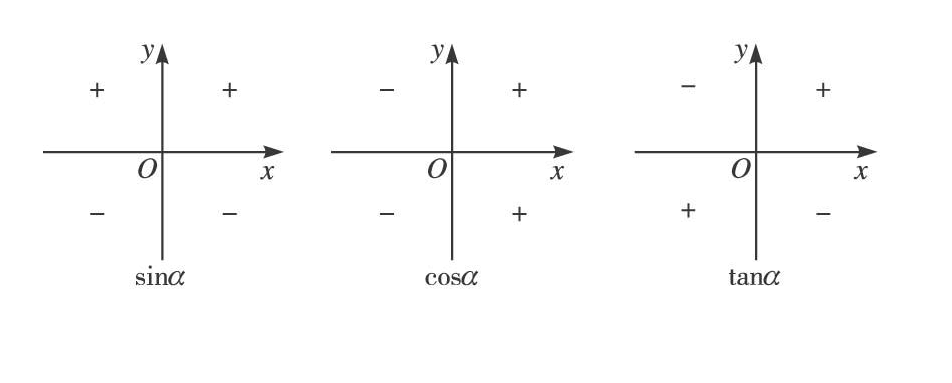
7、三角函数值的符号由角的终边位置即终边所处的象限或轴线来确定。

三角函数线与求角的范围

视频：三角函数线与求角的范围

8、三角函数线是通过形的方式来表示三角函数值的大小。主要有两方面应用：

(1)在求解三角函数值范围时，准确、方便。

(2)为画三角函数图像提供工具。

9、三角函数线概念理解要点如下：

(1)三角函数线是有向线段。

(2)正弦线起点是垂足、终点是角的终边与单位圆的交点。余弦线的起点是原点，终点是垂足。正切线的起点是点(1，0)，终点是切线与角的终边交点。

(3)三角函数线的长度等于三角函数值的大小，三角函数线方向与坐标轴方向相同时函数值为正，相反时函数值为负。

10、在弧度制下，角为锐角时，角度、正弦、正切大小如下图。

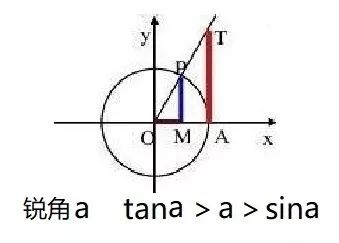
11、三角函数定义的三种形式有内在联系，解答问题时取用何种形式，由问题情境决定。