张量转化成矩阵_代数学发展史: 张量代数

在高等代数课程中遇到的很多概念, 如行列式、矩阵、线性映射、线性变换、双线性函数和内积等, 都可以统一用一个非常重要的概念来表述, 这就是张量, 它在代数、几何、分析及物理等领域有广泛应用. 张量理论的发展要归功于两个意大利数学家——Gregorio Ricci-Curbastro (里奇, 1853–1925) 和他的学生Levi-Civita (1873–1941). 

   

学过现代微分几何的都知道Levi-Civita 联络; 而Ricci 的大名更是如雷灌耳, Perelman 对Poincarè 的证明正是基于一个被称为Ricci 流的概念. 当然, Ricci 流实际上是R. Hamilton 与1981 年提出的, 不过其中的核心概念Ricci 曲率张量的确归功于Ricci. 1890 年, Ricci系统地发展了后来被称为张量分析的理论, Levi-Civita在1900 年将该理论发扬光大并为世人所知, Einstein 在1915 年提出的广义相对论完全是用张量的语言写出的.

据个人经验，本文的内容对于初学者来说非常重要，尽快习惯张量的语言对于深入代数、微分几何等领域是很有帮助的. 

张量积

张量可以看作是标量、向量、矩阵等概念的推广, 标量是0 阶张量, 向量是一阶张量, 而矩阵就是二阶张量. 如果把矩阵推广到高阶就是高阶张量, 而高阶张量实际上是由低阶张量利用一种乘法运算——张量积——得到的. 我们来看看如何由一阶张量即向量得到二阶张量.

理解张量积的最自然的方式可能是从双线性函数的角度来看. 设V,W 为域F 上的线性空间, 称二元函数h(α, β) 为V × W 上的双线性函数, 如果对任意有

双线性函数的全体自然构成一个线性空间B.

一个很自然的构造双线性函数的方法是取, 定义

容易验证h 是双线性函数, 记为f ⊗ g, 称为f 与g 的张量积. 所有形如f ⊗ g 生成的B 的子空间记为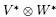, 即

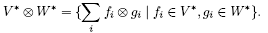
我们称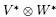为V 与W 的张量积, 其中的元素称为张量. 需要注意的是: 上述定义中的求和是有限和, 并且 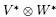中的元素不一定能写成f ⊗ g 的形式, 而通常是一个线性组合.

我们知道, 任何线性空间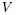都可以看作的对偶空间的子空间, 即对任意