多元函数泰勒级数展开_函数y=3^x的几种幂级数展开

函数幂级数展开公式

设函数f(x)在 x0的某个邻域O(x0 ，r)中能展开幂级数，则它的幂级数展开就是f(x)在x0 的泰勒级数：

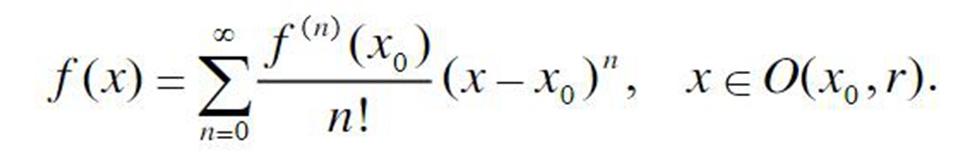
函数y=e^x的幂级数展开

利用函数的幂级数展开公式，其中x0=0，得：

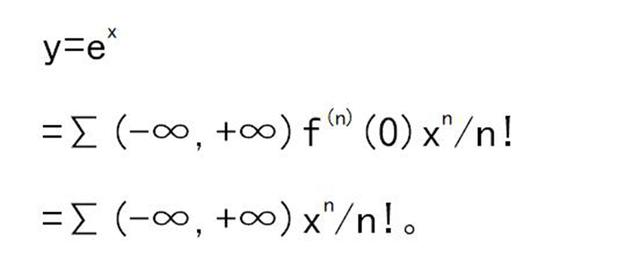
​函数y=3^x在x=0处的幂级数

y=3^x=e^xln3.利用y=e^x的展开公式，则：

y=3^x

=∑(-∞,+∞)(x*ln3)^n/n!,

=∑(-∞,+∞)(ln3)^n*x^n/n!。

函数y=3^x在x-1处的幂级数展开

y=3^x=3*3^x-1=3*e^(x-1)ln3，

则：y=3^x

=3*∑(-∞,+∞)[(x-1)*ln3]n/n!,

=3*∑(-∞,+∞)(ln3)^n*(x-1)^n/n!。

函数y=3^x在2x-1处的幂级数展开

y=3^x=√3*(√3)^2x-1=√3*e^(2x-1)ln√3.

则：y=3^x

=√3*∑(-∞,+∞)[(2x-1)*ln√3]^n/n!,

=√3*∑(-∞,+∞)(ln√3)^n*(2x-1)^n/n!。

函数y=3^sinx在x=0处的幂级数展开

利用y=e^x的展开公式，则：

y=3^sinx=e^ln3*sinx

=∑(-∞,+∞)(ln3*sinx)^n/n!,

=∑(-∞,+∞)(ln3)^n*(sinx)^n/n!。