matlab代数方程,Matlab——数值计算——单个代数方程 代数方程组

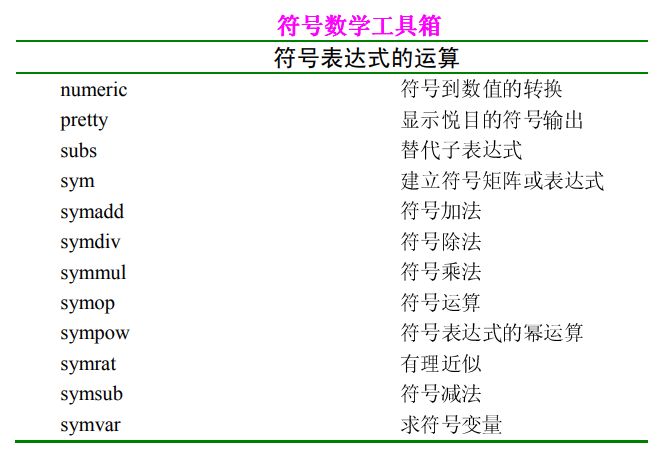
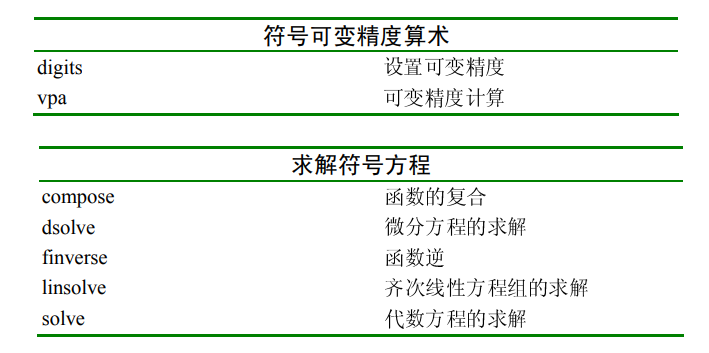
方程求解

求解单个代数方程

MATLAB具有求解符号表达式的工具,如果表达式不是一个方程式(不含等 号)，则在求解之前函数solve将表达式置成等于0。

>>syms a

syms b

syms c

syms x>> solve('a*x^2+b*x+c')

ans=

-(b + (b^2 - 4*a*c)^(1/2))/(2*a)-(b - (b^2 - 4*a*c)^(1/2))/(2*a)

结果是符号向量，其元素是方程的两个解。如果想对非缺省值x变量求解，solve必须指定变量

>> solve('a*x^2+b*x+c','b')

ans=

-(a*x^2 + c)/x

带有等号的符号方程也可以求解:

>> f = solve('cos(x) = sin(x)')

f=pi/4

>> t = solve('tan(2*x) = sin(x)')

t=

0

>> x = solve('exp(x) = tan(x)')

警告: Cannot solve symbolically. Returning a numeric

approximation instead.%不能用符号来解决。返回数字是近似值。

x=

-226.19467105846511316931032359612

代数方程组求解

>> eq1 = 'x-3 =4';

eq2= 'x*2-x-6=0';

eq3= 'x^2+2*x+4=0';

eq4= '3*x+2*y-z=10';

eq5= '-x+3*y+2*z=5';

eq6='x-y-z=-1';>>solve(eq1)

ans=

7

>>solve(eq2)

ans=

6

>>solve(eq3)

ans=

- 3^(1/2)*i - 1

3^(1/2)*i - 1

>>solve(eq4,eq5,eq6)

ans=x: [1x1 sym]

y: [1x1 sym]

z: [1x1 sym]

这里，solve(eq4,eq5,eq6)是一个结构数组，其中每个元素为一符号类型的量：

>> ff =solve(eq4,eq5,eq6);>>ff.x

ans=

-2

>>ff.y

ans=

5

>>ff.z

ans=

-6

也可以：

>> [a,b,c] =solve(eq4,eq5,eq6)

a=

-2b=

5c=

-6

例题：

解题思路：

首先，根据以上给出的信息列出一组线性方程，假如p，n，d和q分别表示1美分，5美分，10美分，和25美分的硬币数

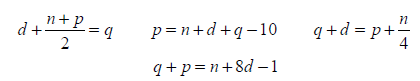
>>syms d>>syms p>>syms n>>syms q>> a = 'd+(n+p)/2=q';>> b = 'p=n+d+q-10';>> c = 'q+d = p+n/4';>> d = 'q+p = n+8*d-1';>> [pennise,nickles,dimes,quarters] = solve(a,b,c,d,'p,n,d,q')

警告: Do not specify equations and variablesas character

strings. Instead, create symbolic variables with syms.

%不要将公式和变量指定为字符串。相反，使用syms创建符号变量。

pennise=

16nickles=

8dimes=

3quarters=

15

>> money = .01*16+.05*8+.10*3+.25*15money=

4.6100

例题：

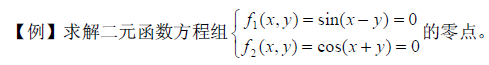
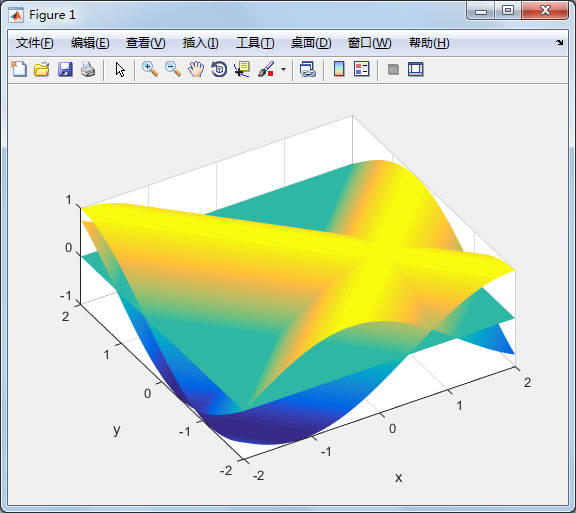
【0】从三维坐标初步观察两函数图形相交情况

x=-2:0.05:2;y=x;[X,Y]=meshgrid(x,y); %产生x-y平面上网点坐标

F1=sin(X-Y);F2=cos(X+Y);

F0=zeros(size(X));

surf(X,Y,F1),

xlabel('x'),ylabel('y'),61view([-31,62]),hold on,

surf(X,Y,F2),surf(X,Y,F0),

shading interp,

hold off

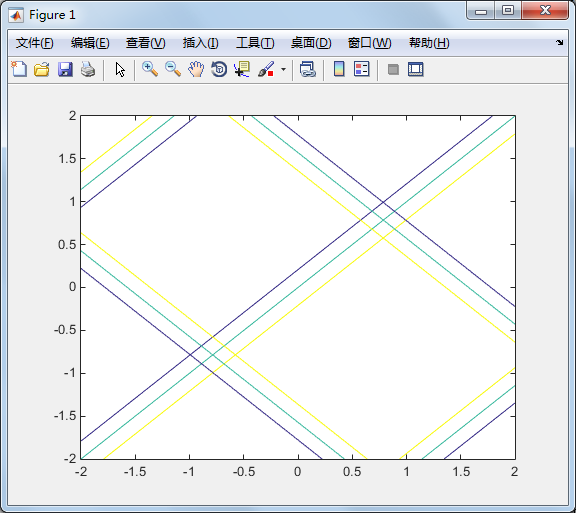
【1】在某区域观察两函数0等位线的交点情况

x=-2:0.5:2;y=x;[X,Y]=meshgrid(x,y); %产生x-y平面上网点坐标

F1=sin(X-Y);F2=cos(X+Y);

v=[-0.2, 0, 0.2]; %指定三个等位值，是为了更可靠地判断0等位线的存在。

contour(X,Y,F1,v)%画F1的三条等位线。

hold on,contour(X,Y,F2,v),hold off%画F2的三条等位线。

【2】从图形获取零点的初始近似值

用ginput 获取两个函数0 等位线(即三线组中间那条线)交点的坐标。

[x0,y0]=ginput(2); %在图上取两个点的坐标

disp([x0,y0])

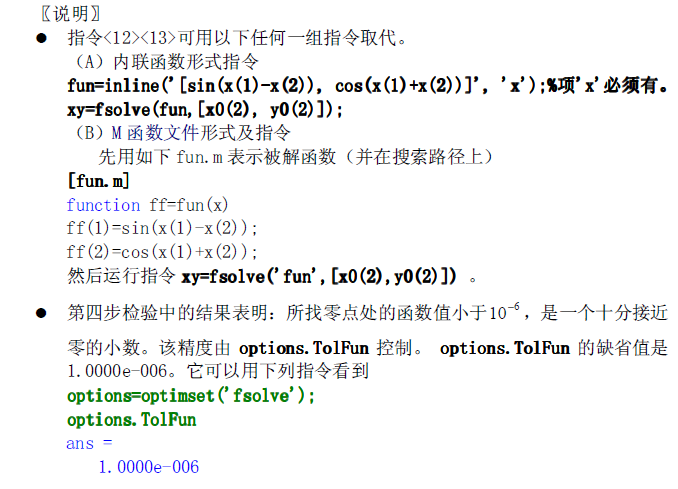
【3】利用 fsolve 求精确解(以求(0.7926,7843)附近的解为例。)

本例直接用字符串表达被解函数。注意：在此，自变量必须写成x(1), x(2)。

假如写成xy(1), xy(2)，指令运行将出错。

fun='[sin(x(1)-x(2)),cos(x(1)+x(2))]'; %<12>xy=fsolve(fun,[x0(2),y0(2)])%<13>

xy =

0.7854 0.7854

【4】检验

fxy1=sin(xy(1)-xy(2));fxy2=cos(xy(1)+xy(2));disp([fxy1,fxy2])