本文介绍了行列式的概念，从二阶行列式的定义出发，阐述了其在解决二元线性方程组中的应用，并逐步拓展到三阶和四阶行列式。通过对角线法则简化计算，强调行列式在求解线性方程组中的重要作用。
本文文字和图片非原创
来源如下↓ 强烈推荐原视频↓
作者：上海交通大学 知名教授 蒋启芬、高云、崔振等
平台： 网易公开课
内容：《线性代数》第一讲 行列式的定义
序言
对二元一次方程组(几何意义：平面上的两条动直线)，通过加减消元可以变形到下边这种形式。?
那么，明显地，如果系数不等于0，我们能快速地得到唯一的一组解。
我们观察一下这个解的形式：比较繁琐，不便记忆和推广，那么可以用一个什么样的符号来代表这一般性的算法呢？
这引导我们先去找到二阶行列式，进而三阶行列式，再到一般的n阶行列式。
开始研究行列式的定义、性质、计算，从而解决用n阶行列式求解n元线性方程组的唯一解的情况。
行列式
2、3阶行列式是如何定义的？
二阶行列式来源于二元一次方程组的求解，通过加减消元得到解。
大家观察一下这个解?：繁琐和不便记忆。这个时候我们怎么办呢？
我们有必要引入一个新的符号，这个新的符号是什么呢？二阶行列式！
现在，我们给出如下二阶行列式的定义：?
我们也把等式的右边叫做二阶行列式的展开式，或二阶行列式的结果。
为了方便记忆这个结果，从视觉效果来看，我们归纳出二阶行列式的对角线法则。?
从左上方到右下方的对角线，称之为主对角线；从右上方到左下方的对角线，称之为副对角线；因此二阶行列式的结果可以简单记为：主乘积与副乘积之差。
现在，有了二阶行列式，我们再回过头看刚才的二元一次方程组，观察解的特征：分子分母都是二阶行列式的结果。
因此，我们就记D(Determinant)来代表这个二阶行列式，正好是方程组的系数排出来的。所以我们又称之为系数行列式。
我们将行列式D中的第一列换成常数项，就构成D1 ；我们将行列式D中的第二列换成常数项，就构成D2。?
因此，对应的解可以写成↓
从这里大家可以领会到，虽然二阶行列式来源于线性方程组的求解，
但反过来，二阶行列式这个工具，使得我们求二元线性方程组的过程，变成了按部就班地进行的程序。
比如说，任意给一个二元线性方程组，我们只需要算出它的系数行列式，然后算出D1 和D2，这样，我们就一般性地实现了两个方程和两个未知数的二元线性方程组的求解。
那么具体到三元线性方程组，我们又该如何去求解？
要解答这个问题，我们想通过加减消元法或者代入消元法，来把它转换为二元线性方程组，利用二阶行列式来求解。
观察三元线性方程组解的形式，我们可以自然地引出?三阶行列式的定义。
它是第一行的所有元素与一个二阶行列式的乘积的代数和。
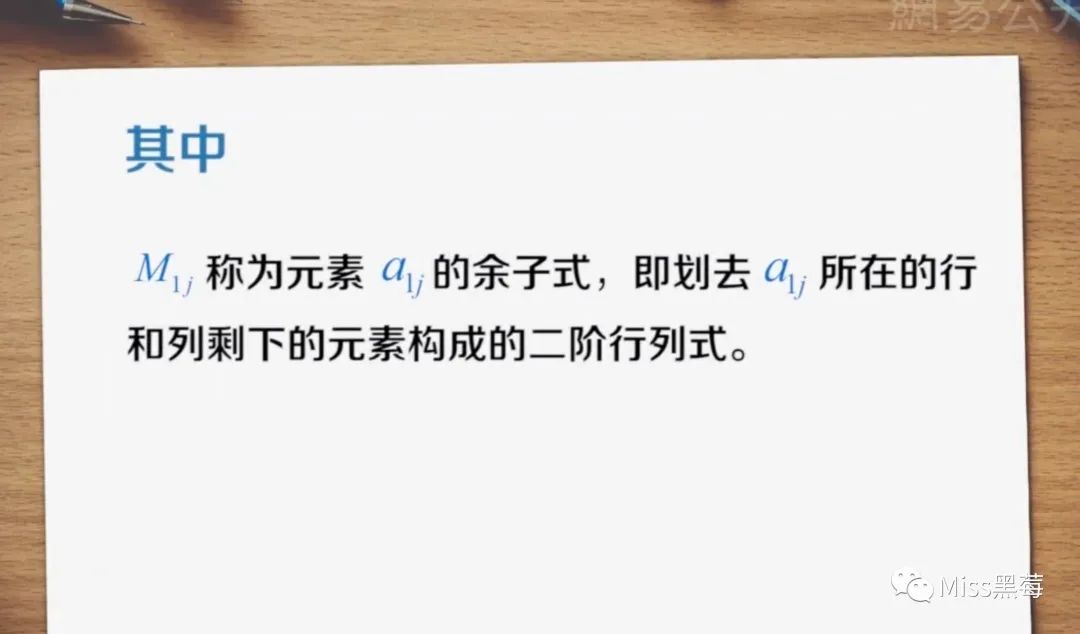
我们把M11 称作a11的余子式……用-1的行列标来体现代数和的式子里的正负号，
因此我们三阶行列式的结果就可以写成?用和号“∑”来表示，看起来就更简洁了。
对于-1的行列标乘以余子式的结果，我们把它称作代数余子式，用大写的A…来表示。
所以我们可以这样描述:三阶行列式的结果等于第一行的元素与各自的代数余子式的乘积之和。
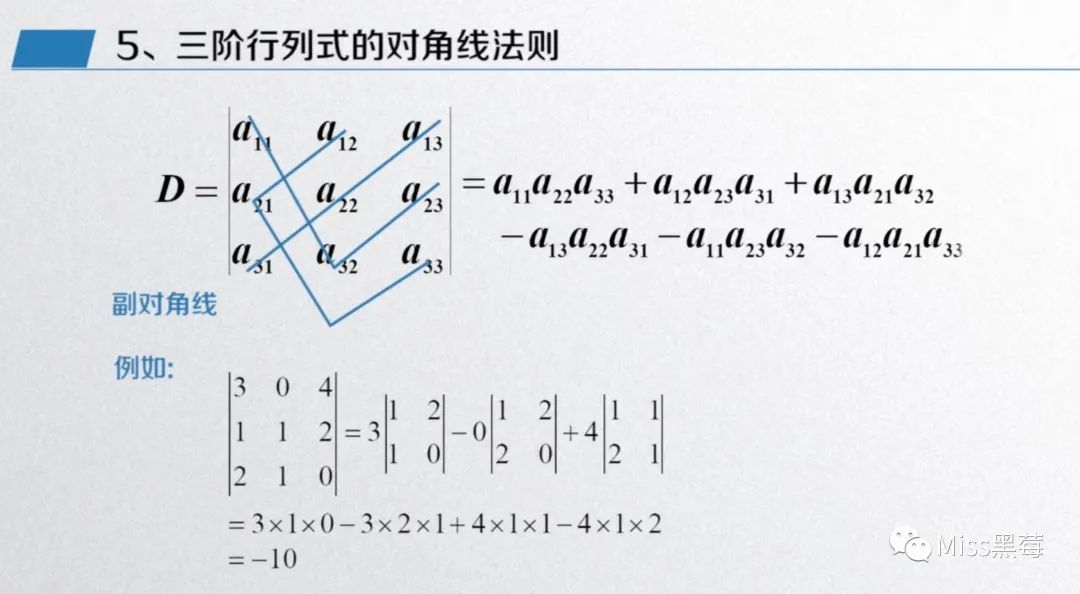
类似二阶行列式，我们也有一个三阶行列式的对角线法则。?
主对角线方向的乘积，减去副对角线方向的乘积。?
因此，对于任意一个行列式，你既可以按照定义转为二阶行列式来计算，又可以直接根据对角线法则来展开得到它的结果。
好，三阶行列式由三元线性方程组引出，而又因为有了三阶行列式这个工具，我们可以更加快捷地求解三元线性方程组了。
那么，一个更进一步的问题又产生了。↓
一个n阶行列式能否用来求解n元线性方程组呢？
这个问题的答案是肯定的。
我们首先需要一个n阶行列式的定义。
从二阶行列式，三阶行列式，我们类推可以定义出四阶行列式，如此推导下去……假如我们n-1阶行列式已经定义好，我们就可以归纳出如下?n阶行列式的定义。
当n=1时，就是一个数。
当n=2时，……
这里要特别注意，或许大家比较好奇：当n＞3时，为什么没有对角线法则呢？
这是因为当大于3时，我们在行列式里面找不到一个对角线法则来符合行列式的通用规律的定义的。所以我们只有按照定义，一阶一阶地往下展开，来计算。
有了n阶行列式的定义，我们可以来求解一些特殊行列式。
好，有了行列式的定义，大家其实可以体会到，如果我们用定义来算一些特殊类型的行列式，尤其是0比较多的行列式，比较快速简便。
若想详细了解上述定义，可以查阅?
扫一扫
3190
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
