头同尾合十的算法_“拉面法”与“头同尾合十”——图解两种速算法

所有算式都是实操的记录。

            ——张益民

Mom always had a way of explaining things so I could understand them.(妈妈总有办法让我明白她的意思。)

            —— Forrest Gump(阿甘)

---

女：爸爸，牛牛同学说乘11可以用“拉面法”速算！

父：什么？拉面法？怎么拉？

女：“两头一拉，中间相加”，你看35×11，把3和5拉开，中间是3和5相加，得385，神奇吧!

父：好神奇啊！那是为啥呢？给我讲讲！

女：嗯，不知道……不过老师还说了一个“头同尾合十”的速算法，

父：“头痛为何事？”，还不是为你写作业头疼？

女：哈哈，不是啦！就是头一个数字相同，末尾的数字相加得十的乘法的速算法，比如 34×36，头都是3，尾巴4+6=10

父：哦，明白了，十位数上相同，个位上数字的和是十的两位数乘法

女：对！

父：怎么个速算法呢？

女：你看啊，把后面这个3加1，得4，在乘前面这个3，得12，再把个位的4×6得24，写在12后面就是1224，快吧？！

父：快！真快！是什么原理呢？

女：不知道……

(能把天聊死的老爹……)

---

隔日，老爹又搬出了宝石箱：

旁白：宝石王国发现了新的蓝宝石矿(感谢呗吟)，第一天就挖出了许多美丽的蓝宝石宝石，矿工们把宝石排成了11行每行23颗，如图：

公主：哇，这蓝宝石真漂亮！还有一行深蓝色的！

国王：真是漂亮，除法公主那里一定能卖得很好！那先请乘法公主帮忙算一算，今天收获了多少颗啊？

公主：深蓝色的一行23颗，浅蓝色的一共10行，23×10就是230颗，一共253颗。(看来上一幕戏没白演，参考《即兴小剧场》)

国王：嗯，那请公主帮忙记录下来吧，

公主：(记录中)

国王：听说有个“拉面法”可以快速的算出宝石的数量，公主能试试吗？(国王还挺潮)

公主：“拉面法”，对哦！“两边一拉，中间相加”,把23的‘2’和‘3’拉开，再用2+3=5，放在‘2’和‘3’中间得 253，(公主边在纸上写着边说，纸上的记录如图，对不住各位，我给这个记录拍照时，已经被弟弟画成这样了)

国王：真的好神奇，那为什么要把2和3拉开呢？

公主：为了放下5啊！

国王：哦，那拉开了从个位、十位、百位的

上看，有什么变化？

公主：(思考了一会……)2到了百位，3还是在个位，5放在了十位，(又思考了一会……)看来不是“两边一拉”，而是“把2推到百位”，3在个位并没有动。

国王：嗯嗯，那“中间相加”呢？

公主：指着竖式中间十位上的2和3，这两个都在十位上，所以相加后的5代表5个十，放百位和个位中间，就是“中间相加”。

国王：的确如此！公主看来已经看透了“拉面法”了呢！那从宝石阵里能看出什么呢？

公主：(把宝石阵，重新排布成这样，如图)这一大块，就是20×10，200颗、20袋，2盒，就是百位上的2；这3颗就是个位上的3.

公主：(指着图中左下和右上的两块说)把这30颗和这20颗相加得50颗，是5袋，就是中间(十位)的5。

国王，(指着深蓝色的的20颗说)可不可以把这20颗移到30颗边上，让他们挨在一起？

公主：好，(把20颗深蓝色的移动到如图位置)这样更清晰了。

国王：那请公主记录一下吧。

公主：(记录中)

隔日……

带领公主不摆宝石、回顾这个过程并整理记录(略)

整理记录完毕，国王拿出网格纸(感谢平平老师，让我发现网格纸这个利器，大的两位数乘法摆宝石实在是辛苦)，如图：

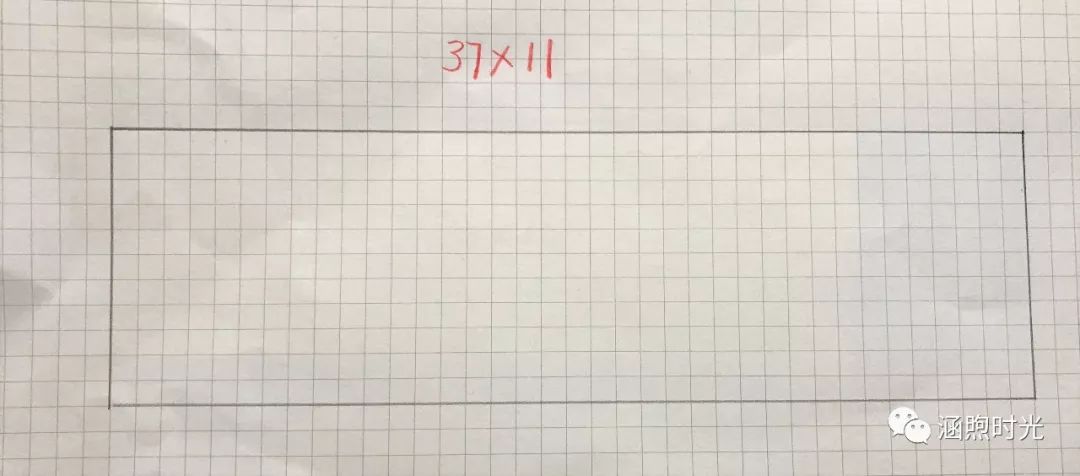
国王：最近国事繁忙，没能带公主去矿场，今天矿工长，将采得得宝石画成了方格图，每个格子里放一块宝石、公主来帮我看看，这上面写着37×11，今天收获了多少颗宝石啊(注意中间相加有进位)。

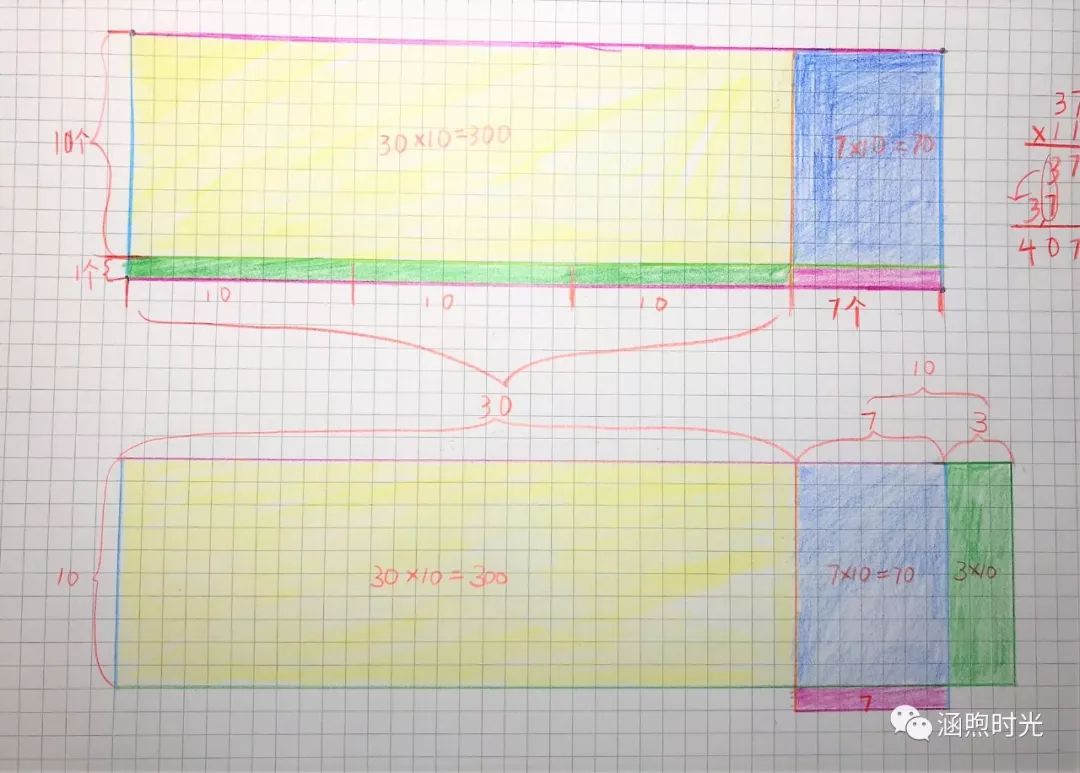
公主：好的！(在方格图上分割如下)

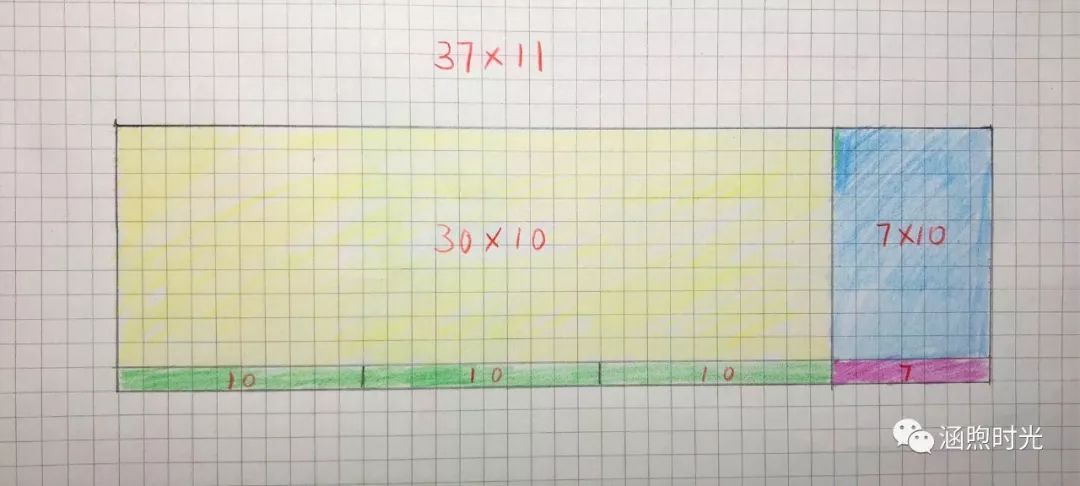
公主：最大这块30×10是300颗，3盒，所以百位上是3，这里面的70颗和30颗相加刚好够了100颗，凑了一盒，所以百位要加一变成4了，我来挪一下。(剪裁移动如下：)

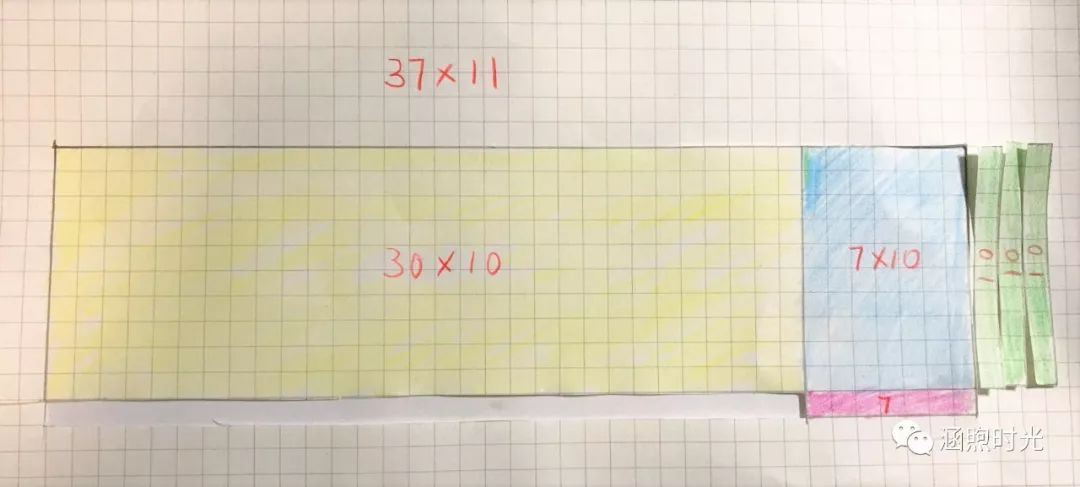
国王：这样清楚多了！看来中间相加可能会有进位呢，会不会进位是2呢？

公主：想了想说，不会的，最多是9+9 = 18，进位最多是1。

国王：原来如此！

公主整理记录如下：

隔日……

带领公主不摆不画图、回顾37×11后，

国王：今天矿工长送来的宝石阵图是这样的，23×27，有劳乘法公主帮我统计一下吧。

公主：这个就是“头同尾合十”啊，2+1=3，2×3=6，加上3×7=21，就是621.

国王：好快啊！那是怎么个道理呢？

公主：(对着方格图，分割着，得到下图)

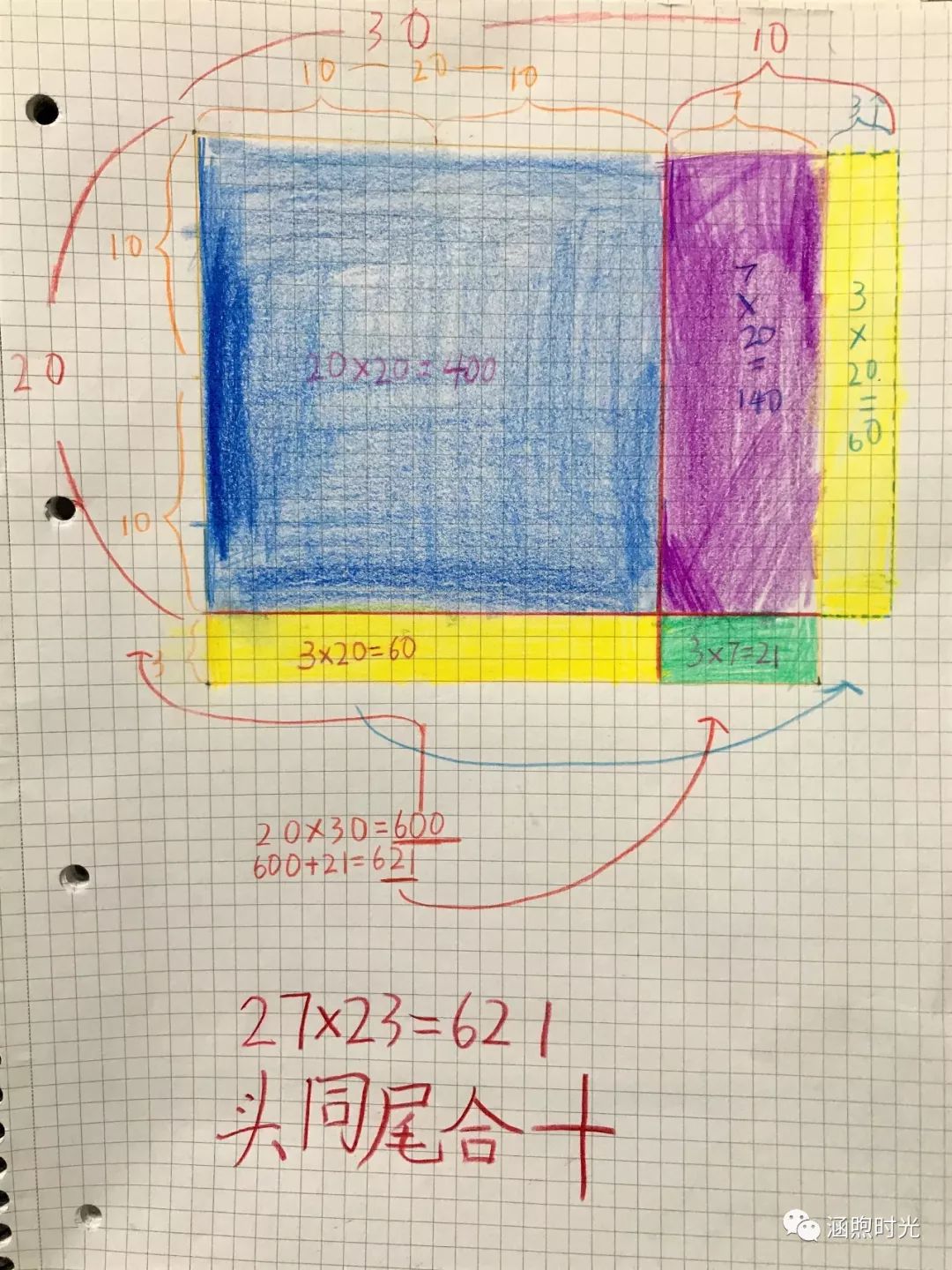
公主：这个小块就是3×7=21就是十位和个位，这个大块是20×20=400颗，嗯……这两块(紫色和黄色)加起来是10×20=200颗。 哦！400+200=600，是6盒，6就是这么来的。

国王：可是你的描绘的过程中，我看到了3×7= 21，我没看到2×3=6啊？

公主：(思考了一会，把3×20(黄色)移到了7×20(紫色)旁边，)这个和“拉面法”有点像。看！(指着图中蓝紫黄合起来的一大块)原来有20个20(蓝色)，这紫色黄色、两块加起来，7个20和3个20又凑出了10个20，现在就有30个20，是20×30，就是十位上的2×3；600个！

国王：哈哈，有意思，有意思！看来“头同尾合十”的速算法可以这么解释啊！请你把她记录下来吧！

公主记录中。

---

后记：

“拉面法”和“头同尾合十”是苏教版《数学》三年级下课本里的两种速算方式，女儿虽然掌握了速算技巧，可是对原理却并不了解，本文试图利用前面带她玩过的宝石游戏，解释两种速算法的计算原理，都是野路子，如有不妥之处，还望各位老师不吝赐教。

---

订正：

在《即兴小剧场——玩转两位数乘两位数竖式运算》发表之后，很多老师给了中肯细致的建议，其中田岚老师指出文中的图并没有与17X13的竖式直接对应，并提供了参考图，如图：

这是我的疏忽，在此向大家致歉，并补充图如下！

另外田老师和林然老师都指出，17×10(两位数乘整十数)从实操到算式的过程没有在文中展示出来；林然老师还建议我们通过唱数练习将17×10视为一整块，这些是都是极有价值的建议，这些天我们爷俩都会通过抛接杂耍球来巩固10的倍数的唱数。再次对两位老师表示诚挚的谢意！