如何判断两个平面相交_一张思维导图搞定高中数学《点、直线、平面之间的位置关系》...

高一数学《点、线、平面之间的位置关系》这一张，很多同学学完后，脑袋一团浆糊，要么感觉什么都没学，要么感觉东西太多了。本文，我们通过一张思维导图帮助大家搞定。首先，一起来看下总体内容，如下图。

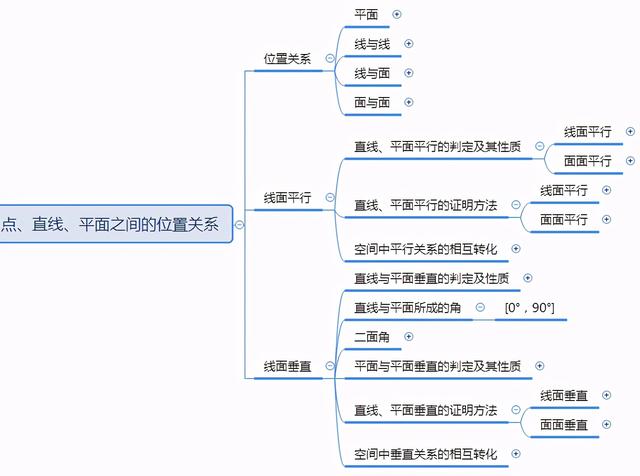
点、直线、平面之间的位置关系思维导图-高中数学思维导图

简单说就是位置关系的考查，重点在于线面平行的判定和性质以及线面垂直的判定和性质。线面垂直部分，注意二面角相关内容，因为在高考立体几何中几乎属于必考内容。

一、 位置关系

位置关系思维导图-高中数学思维导图

担心图文看不清晰，我们将重要内容摘录如下，需要xmind思维导图原图复习的同学，记得文末留言即可。

平面的基本性质(三大公理)：

①A∈l，B∈l，且A∈α，B∈α → l 包含于 α。

直线上两点在平面内，直线在此平面内。

②过不在同一条直线上的三点有且仅有一个平面。不共线的三点确定一个平面。

③如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

公理②有三条推论：

推论一：经过一条直线和直线外一点，有且只有一个平面。

推论二：经过两条相交直线，有且只有一个平面。

推论三：经过两条平行直线，有且只有一个平面。

二、 线面平行

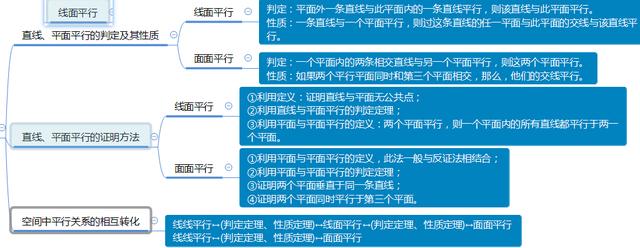
线面平行思维导图-高中数学思维导图

1. 线面平行

判定：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

性质：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。

证明方法：

①利用定义：证明直线与平面无公共点；

②利用直线与平面平行的判定定理；

③利用平面与平面平行的定义：两个平面平行，则一个平面内的所有直线都平行于两一个平面。

2. 面面平行

判定：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

性质：如果两个平行平面同时和第三个平面相交，那么，他们的交线平行。

证明方法：

①利用平面与平面平行的定义，此法一般与反证法相结合；

②利用平面与平面平行的判定定理；

③证明两个平面垂直于同一条直线；

④证明两个平面同时平行于第三个平面。

三、 线面垂直

线面垂直思维导图-高中数学思维导图

1. 线面垂直的证明

①利用直线与平面垂直的定义(可以用反证法)；

②利用直线与平面垂直的判定定理；

③利用平面与平面垂直的性质定理；

④结合平行关系： A：a//b，a⊥α→b⊥α； B：a⊥α，α//β，a⊥β

1. 面面垂直的证明

①利用定义判断(证明)二面角的平面角是直角；

②利用平面与平面垂直的判定定理。

本文就给大家梳理到此，下期继续更新第三章《直线与方程》章节。敬请期待，需要x mind原图的文末留言即可。